Count of binary arrays of size N with sum of product of adjacent pairs equal to K

Given two integers N and K, the task is to find the total number of possible binary array of size N such that the sum of the product of adjacent pairs in that array is exactly equal to K.

Examples:

Input: N = 5, K = 3
Output: 2
Explanation: Two combinations of array A of size N, whose sum of product of adjacent pairs adds up to K=3.
A = [1, 1, 1, 1, 0]: Value =  (1*1) + (1*1) + (1*1) + (1*0) = 3
A = [0, 1, 1, 1, 1]: Value =  (0*1) + (1*1) + (1*1) + (1*1) = 3

Input: N = 5, K = 4
Output: 1
Explanation: 
A = [1, 1, 1, 1, 1]: Value =  (1*1) + (1*1) + (1*1) + (1*1) = 4

Input: N=2, K=3
Output: 0

Naive Approach: The simplest approach is to find all the possible combinations of the array possible, and checking each combination individually that if its sum is equal to K or not.
Time Complexity: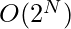

Efficient Approach:  Above explained simple approach can be optimized by memoising the result of each recursive call in a 3d matrix dp of size (K+1, N+1, 2), i.e. dp[K+1][N+1][2]. Here, each node of this dp matrix, say dp[a][b] represents the number of combinations possible of size b having sum a and last element is c where c can only be 0 or 1. Now follow the below steps to solve this problem:

1. First, create a function combinationsPossible with parameters (N, idx, prev, val, K), where N is the size of the array to be formed, idx is the index till which all possible combinations of the array are possible (initially 0), prev is the previous element in the newly formed array(can only be 0 or 1), val is the sum of products till idx and K is the sum of the product of consecutive elements. This function will return the number of possible combinations till index idx having sum val and previous element prev. Also, memoise the result while returning.
2. Now, from the main function call the above-stated function combinationsPossible two times with all the initial values same but only changing prev to 0 in one and 1 in another to calculate the combinations possible of all the arrays starting from 0 and 1.
3. In each call check for the base cases, that are:
   • If val>K: return 0, because after this index there are 0 combinations having sum K as the sum already exceeded.
   • If idx=N-1: this means that the whole array of size N is formed. So just return 1 i.e. number of combinations possible, if the val is K. Otherwise, return 0.
4. Also, in each recursive call check if its result is already memoised or not. If it is, then just return that from the dp array.
5. Now if the previous element is 1, make two recursive calls:
   • To consider the combinations possible with 1 as the current element. So, increase val by 1 in this call because the product of both current and previous element (1*1=1) will add 1 to the current sum.
   • To consider the combinations possible with 0 as the current element. In this case, val will remain the same.
6. If the previous element is 0, then also make two recursive calls, one to consider the combinations with 1 as the current element and another to consider the combinations with 0 as the current element. In both cases, val will remain the same.
7. Add all the values returned by the above four function calls and return this added value from the current function after memoising.
8. Print the answer according to the above observation.

Below is the implementation of the above approach:

C++

// C++ program for the above approach

#include <bits/stdc++.h>
using namespace std;

// Function to return the number of total
// possible combinations of 0 and 1 to form
// an array of size N having sum of product
// of consecutive elements K
int combinationsPossible(int N, int idx, int prev, int val,
                         int K,
                         vector<vector<vector<int> > >& dp)
{

    // If value is greater than K, then
    // return 0 as no combination is
    // possible to have sum K
    if (val > K) {
        return 0;
    }

    // Check if the result of this recursive
    // call is memoised already, if it is then
    // just return the previously calculated result
    if (dp[val][idx][prev] != -1) {
        return dp[val][idx][prev];
    }

    // Check if the value is equal to K at N, if
    // it is then return 1 as this combination
    // is possible. Otherwise return 0.
    if (idx == N - 1) {
        if (val == K) {
            return 1;
        }
        return 0;
    }
    int ans = 0;

    // If previous element is 1
    if (prev == 1) {

        // If current element is 1 as well, then
        // add 1 to value
        ans += combinationsPossible(N, idx + 1, 1, val + 1,
                                    K, dp);

        // If current element is 0, then value
        // will remain same
        ans += combinationsPossible(N, idx + 1, 0, val, K,
                                    dp);
    }

    // If previous element is 0, then value will
    // remain same irrespective of the current element
    else {
        ans += combinationsPossible(N, idx + 1, 1, val, K,
                                    dp);
        ans += combinationsPossible(N, idx + 1, 0, val, K,
                                    dp);
    }

    // Memoise and return the ans
    return dp[val][idx][prev] = ans;
}

// Driver Code
int main()
{
    int N = 5;
    int K = 3;
    vector<vector<vector<int> > > dp(
        K + 1,
        vector<vector<int> >(N + 1, vector<int>(2, -1)));

    // As the array can be started by 0 or 1, so take both
    // cases while calculating the total possible
    // combinations
    cout << (combinationsPossible(N, 0, 0, 0, K, dp)
             + combinationsPossible(N, 0, 1, 0, K, dp));
}

Java

// Java program for the above approach
import java.util.*;

class GFG
{

    // Function to return the number of total
    // possible combinations of 0 and 1 to form
    // an array of size N having sum of product
    // of consecutive elements K
    static int combinationsPossible(int N, int idx, int prev,
                                    int val, int K, int[][][] dp)
    {

        // If value is greater than K, then
        // return 0 as no combination is
        // possible to have sum K
        if (val > K) {
            return 0;
        }

        // Check if the result of this recursive
        // call is memoised already, if it is then
        // just return the previously calculated result
        if (dp[val][idx][prev] != -1) {
            return dp[val][idx][prev];
        }

        // Check if the value is equal to K at N, if
        // it is then return 1 as this combination
        // is possible. Otherwise return 0.
        if (idx == N - 1) {
            if (val == K) {
                return 1;
            }
            return 0;
        }
        int ans = 0;

        // If previous element is 1
        if (prev == 1) {

            // If current element is 1 as well, then
            // add 1 to value
            ans += combinationsPossible(N, idx + 1, 1, val + 1, K, dp);

            // If current element is 0, then value
            // will remain same
            ans += combinationsPossible(N, idx + 1, 0, val, K, dp);
        }

        // If previous element is 0, then value will
        // remain same irrespective of the current element
        else {
            ans += combinationsPossible(N, idx + 1, 1, val, K, dp);
            ans += combinationsPossible(N, idx + 1, 0, val, K, dp);
        }

        // Memoise and return the ans
        dp[val][idx][prev] = ans;
        return dp[val][idx][prev];
    }

    // Driver Code
    public static void main(String[] args) {
        int N = 5;
        int K = 3;
        int[][][] dp = new int[K + 1][N + 1][2];
        for (int i = 0; i < K + 1; i++) {
            for (int j = 0; j < N + 1; j++) {
                for (int k = 0; k < 2; k++)
                    dp[i][j][k] = -1;
            }
        }

        // As the array can be started by 0 or 1, so take both
        // cases while calculating the total possible
        // combinations
        System.out.print(combinationsPossible(N, 0, 0, 0, K, dp) + combinationsPossible(N, 0, 1, 0, K, dp));
    }
}

// This code is contributed by 29AjayKumar

Python3

# Python 3 program for the above approach

# Function to return the number of total
# possible combinations of 0 and 1 to form
# an array of size N having sum of product
# of consecutive elements K
def combinationsPossible(N, idx, prev, val, K, dp):
    # If value is greater than K, then
    # return 0 as no combination is
    # possible to have sum K
    if (val > K):
        return 0

    # Check if the result of this recursive
    # call is memoised already, if it is then
    # just return the previously calculated result
    if (dp[val][idx][prev] != -1):
        return dp[val][idx][prev]

    # Check if the value is equal to K at N, if
    # it is then return 1 as this combination
    # is possible. Otherwise return 0.
    if (idx == N - 1):
        if(val == K):
            return 1
        return 0
    ans = 0

    # If previous element is 1
    if (prev == 1):
        # If current element is 1 as well, then
        # add 1 to value
        ans += combinationsPossible(N, idx + 1, 1, val + 1, K, dp)

        # If current element is 0, then value
        # will remain same
        ans += combinationsPossible(N, idx + 1, 0, val, K, dp)

    # If previous element is 0, then value will
    # remain same irrespective of the current element
    else:
        ans += combinationsPossible(N, idx + 1, 1, val, K, dp)
        ans += combinationsPossible(N, idx + 1, 0, val, K, dp)

    # Memoise and return the ans
    dp[val][idx][prev] = ans
    return ans

# Driver Code
if __name__ == '__main__':
    N = 5
    K = 3
    dp = [[[-1 for i in range(2)] for j in range(N+1)] for k in range(K+1)]
    # As the array can be started by 0 or 1, so take both
    # cases while calculating the total possible
    # combinations
    print(combinationsPossible(N, 0, 0, 0, K, dp) + combinationsPossible(N, 0, 1, 0, K, dp))

    # This code is contributed by SURENDRA_GANGWAR.

C#

// C# program for the above approach
using System;
class GFG
{

    // Function to return the number of total
    // possible combinations of 0 and 1 to form
    // an array of size N having sum of product
    // of consecutive elements K
    static int combinationsPossible(int N, int idx,
                                    int prev, int val,
                                    int K, int[, , ] dp)
    {

        // If value is greater than K, then
        // return 0 as no combination is
        // possible to have sum K
        if (val > K) {
            return 0;
        }

        // Check if the result of this recursive
        // call is memoised already, if it is then
        // just return the previously calculated result
        if (dp[val, idx, prev] != -1) {
            return dp[val, idx, prev];
        }

        // Check if the value is equal to K at N, if
        // it is then return 1 as this combination
        // is possible. Otherwise return 0.
        if (idx == N - 1) {
            if (val == K) {
                return 1;
            }
            return 0;
        }
        int ans = 0;

        // If previous element is 1
        if (prev == 1) {

            // If current element is 1 as well, then
            // add 1 to value
            ans += combinationsPossible(N, idx + 1, 1,
                                        val + 1, K, dp);

            // If current element is 0, then value
            // will remain same
            ans += combinationsPossible(N, idx + 1, 0, val,
                                        K, dp);
        }

        // If previous element is 0, then value will
        // remain same irrespective of the current element
        else {
            ans += combinationsPossible(N, idx + 1, 1, val,
                                        K, dp);
            ans += combinationsPossible(N, idx + 1, 0, val,
                                        K, dp);
        }

        // Memoise and return the ans
        return dp[val, idx, prev] = ans;
    }

    // Driver Code
    public static void Main()
    {
        int N = 5;
        int K = 3;
        int[, , ] dp = new int[K + 1, N + 1, 2];
        for (int i = 0; i < K + 1; i++)
            for (int j = 0; j < N + 1; j++)
                for (int l = 0; l < 2; l++)
                    dp[i, j, l] = -1;

        // As the array can be started by 0 or 1, so take
        // both cases while calculating the total possible
        // combinations
        Console.WriteLine(
            combinationsPossible(N, 0, 0, 0, K, dp)
            + combinationsPossible(N, 0, 1, 0, K, dp));
    }
}

// This code is contributed by ukasp.

Javascript

<script>
        // JavaScript Program to implement
        // the above approach

        // Function to return the number of total
        // possible combinations of 0 and 1 to form
        // an array of size N having sum of product
        // of consecutive elements K
        function combinationsPossible(N, idx, prev, val,
            K,
            dp) {

            // If value is greater than K, then
            // return 0 as no combination is
            // possible to have sum K
            if (val > K) {
                return 0;
            }

            // Check if the result of this recursive
            // call is memoised already, if it is then
            // just return the previously calculated result
            if (dp[val][idx][prev] != -1) {
                return dp[val][idx][prev];
            }

            // Check if the value is equal to K at N, if
            // it is then return 1 as this combination
            // is possible. Otherwise return 0.
            if (idx == N - 1) {
                if (val == K) {
                    return 1;
                }
                return 0;
            }
            let ans = 0;

            // If previous element is 1
            if (prev == 1) {

                // If current element is 1 as well, then
                // add 1 to value
                ans += combinationsPossible(N, idx + 1, 1, val + 1,
                    K, dp);

                // If current element is 0, then value
                // will remain same
                ans += combinationsPossible(N, idx + 1, 0, val, K,
                    dp);
            }

            // If previous element is 0, then value will
            // remain same irrespective of the current element
            else {
                ans += combinationsPossible(N, idx + 1, 1, val, K,
                    dp);
                ans += combinationsPossible(N, idx + 1, 0, val, K,
                    dp);
            }

            // Memoise and return the ans
            return dp[val][idx][prev] = ans;
        }

        // Driver Code
        let N = 5;
        let K = 3;
        let dp = new Array(K + 1);
        for (i = 0; i < dp.length; i++) {
            dp[i] = new Array(N + 1);
        }
        for (i = 0; i < dp.length; i++) {
            for (j = 0; j < dp[0].length; j++) {
                dp[i][j] = new Array(2).fill(-1);
            }
        }

        // As the array can be started by 0 or 1, so take both
        // cases while calculating the total possible
        // combinations
        document.write(combinationsPossible(N, 0, 0, 0, K, dp)
            + combinationsPossible(N, 0, 1, 0, K, dp));

     // This code is contributed by Potta Lokesh
    </script>

Output

2

Time Complexity: O(N*K)

Space Complexity : O(2*N*K)

Iterative Dynamic Programming Approach:

This approach to solve the problem is similar to the previous efficient one except one thing which is here iteratively we will be storing states of dp instead of recurring and memoising it. Here, each node of this dp matrix, say dp[a][b] represents the number of combinations possible of size b having sum a and last element is c where c can only be 0 or 1. Now follow the below steps to solve this problem

Below is the implementation of the above approach:

C++

// C++ code for the approach

#include <bits/stdc++.h>
#include <vector>
using namespace std;

// Function to return the number of total
// possible combinations of 0 and 1 to form
// an array of size N having sum of product
// of consecutive elements K
int combinationsPossible(int N, int K)
{
    vector<vector<vector<int> > > dp(
        K + 1,
        vector<vector<int> >(N + 1, vector<int>(2, -1)));

    // Base case when N is 0
    for (int k = 0; k <= K; k++) {
        dp[k][0][0] = (k == 0) ? 1 : 0;
        dp[k][0][1] = 0;
    }

    // Calculate the DP table iteratively
    for (int n = 1; n <= N; n++) {
        for (int k = 0; k <= K; k++) {
            for (int prev = 0; prev <= 1; prev++) {
                dp[k][n][prev] = 0;
                if (prev == 1) {
                    // If the previous element is 1,
                    // the current element can be either 0
                    // or 1
                    if (k - 1 >= 0) {
                        dp[k][n][prev]
                            += dp[k - 1][n - 1][1];
                    }
                    dp[k][n][prev] += dp[k][n - 1][0];
                }
                else {
                    // If the previous element is 0,
                    // the current element can be either 0
                    // or 1
                    dp[k][n][prev] += dp[k][n - 1][1];
                    dp[k][n][prev] += dp[k][n - 1][0];
                }
            }
        }
    }

    // Return the total number of combinations
    return dp[K][N][0] + dp[K][N][1];
}

// Driver Code
int main()
{
    int N = 5;
    int K = 3;

    // Function call
    cout << combinationsPossible(N, K) << endl;

    return 0;
}

Java

import java.util.Arrays;

class GFG {
    // Function to return the number of total
    // possible combinations of 0 and 1 to form
    // an array of size N having sum of product
    // of consecutive elements K
    static int combinationsPossible(int N, int K)
    {
        int[][][] dp = new int[K + 1][N + 1][2];

        // Base case when N is 0
        for (int k = 0; k <= K; k++) {
            dp[k][0][0] = (k == 0) ? 1 : 0;
            dp[k][0][1] = 0;
        }

        // Calculate the DP table iteratively
        for (int n = 1; n <= N; n++) {
            for (int k = 0; k <= K; k++) {
                for (int prev = 0; prev <= 1; prev++) {
                    dp[k][n][prev] = 0;
                    if (prev == 1) {
                        // If the previous element is 1,
                        // the current element can be either
                        // 0 or 1
                        if (k - 1 >= 0) {
                            dp[k][n][prev]
                                += dp[k - 1][n - 1][1];
                        }
                        dp[k][n][prev] += dp[k][n - 1][0];
                    }
                    else {
                        // If the previous element is 0,
                        // the current element can be either
                        // 0 or 1
                        dp[k][n][prev] += dp[k][n - 1][1];
                        dp[k][n][prev] += dp[k][n - 1][0];
                    }
                }
            }
        }

        // Return the total number of combinations
        return dp[K][N][0] + dp[K][N][1];
    }

    // Driver Code
    public static void main(String[] args)
    {
        int N = 5;
        int K = 3;

        // Function call
        System.out.println(combinationsPossible(N, K));
    }
}
// This code is contributed by rambabuguphka

Python

# Function to return the number of total
# possible combinations of 0 and 1 to form
# an array of size N having sum of product
# of consecutive elements K
def combinations_possible(N, K):
    dp = [[[0 for _ in range(2)] for _ in range(N + 1)] for _ in range(K + 1)]

    # Base case when N is 0
    for k in range(K + 1):
        dp[k][0][0] = 1 if k == 0 else 0
        dp[k][0][1] = 0

    # Calculate the DP table iteratively
    for n in range(1, N + 1):
        for k in range(K + 1):
            for prev in range(2):
                dp[k][n][prev] = 0
                if prev == 1:
                    # If the previous element is 1,
                    # the current element can be either 0
                    # or 1
                    if k - 1 >= 0:
                        dp[k][n][prev] += dp[k - 1][n - 1][1]
                    dp[k][n][prev] += dp[k][n - 1][0]
                else:
                    # If the previous element is 0,
                    # the current element can be either 0
                    # or 1
                    dp[k][n][prev] += dp[k][n - 1][1]
                    dp[k][n][prev] += dp[k][n - 1][0]

    # Return the total number of combinations
    return dp[K][N][0] + dp[K][N][1]

# Driver Code
def main():
    N = 5
    K = 3

    # Function call
    print(combinations_possible(N, K))

if __name__ == "__main__":
    main()

C#

using System;

class GFG {
// Function to return the number of total
// possible combinations of 0 and 1 to form
// an array of size N having sum of product
// of consecutive elements K
    static int CombinationsPossible(int N, int K)
    {
        // Create a 3D DP array to store the combinations
        // count
        int[][][] dp = new int[K + 1][][];
        for (int i = 0; i <= K; i++) {
            dp[i] = new int[N + 1][];
            for (int j = 0; j <= N; j++) {
                dp[i][j] = new int[2];
                for (int k = 0; k < 2; k++) {
                    dp[i][j][k]
                        = -1; // Initialize DP values to -1
                }
            }
        }

        // Base case: when n=0, number of combinations is 1
        // when k=0, otherwise 0
        for (int k = 0; k <= K; k++) {
            dp[k][0][0] = (k == 0) ? 1 : 0;
            dp[k][0][1] = 0;
        }

        // Fill the DP table using the recurrence relation
        for (int n = 1; n <= N; n++) {
            for (int k = 0; k <= K; k++) {
                for (int prev = 0; prev <= 1; prev++) {
                    dp[k][n][prev] = 0;

                    // Calculate combinations based on the
                    // previous state (prev)
                    if (prev == 1) {
                        if (k - 1 >= 0) {
                            dp[k][n][prev]
                                += dp[k - 1][n - 1]
                                     [1]; // Choose n and k
                        }
                        dp[k][n][prev]
                            += dp[k][n - 1]
                                 [0]; // Do not choose n
                    }
                    else {
                        dp[k][n][prev]
                            += dp[k][n - 1][1]; // Choose n
                        dp[k][n][prev]
                            += dp[k][n - 1]
                                 [0]; // Do not choose n
                    }
                }
            }
        }

        // Return the total count of combinations for K
        // items from N numbers
        return dp[K][N][0] + dp[K][N][1];
    }

    static void Main(string[] args)
    {
        int N = 5; // Number of items (5 numbers)
        int K = 3; // Number of items to choose (3
                   // combinations)

        // Print the total number of possible combinations
        Console.WriteLine(CombinationsPossible(N, K));
    }
}

Javascript

function GFG(N, K) {
    // Initialize a 3D DP array with default values
    const dp = new Array(K + 1)
        .fill(0)
        .map(() =>
            new Array(N + 1)
                .fill(0)
                .map(() => new Array(2).fill(-1))
        );
    // Base case when N is 0
    for (let k = 0; k <= K; k++) {
        dp[k][0][0] = k === 0 ? 1 : 0;
        dp[k][0][1] = 0;
    }
    // Calculate the DP table iteratively
    for (let n = 1; n <= N; n++) {
        for (let k = 0; k <= K; k++) {
            for (let prev = 0; prev <= 1; prev++) {
                dp[k][n][prev] = 0;
                if (prev === 1) {
                    // If the previous element is 1
                    if (k - 1 >= 0) {
                        dp[k][n][prev] += dp[k - 1][n - 1][1];
                    }
                    dp[k][n][prev] += dp[k][n - 1][0];
                } else {
                    // If the previous element is 0
                    // the current element can be either 0 or 1
                    dp[k][n][prev] += dp[k][n - 1][1];
                    dp[k][n][prev] += dp[k][n - 1][0];
                }
            }
        }
    }
    return dp[K][N][0] + dp[K][N][1];
}
// Driver Code
const N = 5;
const K = 3;
// Function call
console.log(GFG(N, K));

Output

2

Time Complexity: O(N*K) since two nested loops are executing one from 1 to N and other from 0 to K where N and K are given inputs.
Auxiliary Space: O(2*N*K) since 3D Dp of size N*K*2 has been created. Here, N and K are given inputs.