Count of all sub-strings with sum of weights at most K
Last Updated :
08 Sep, 2021
Given a string S consisting of small English letters and a string W consisting of weight of all characters of English alphabet where for all i,
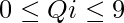
. We have to find the total numbers of a unique substring with sum of weights at most K.
Examples:
Input : P = “ababab”, Q = “12345678912345678912345678”, K=5
Output : 7
Explanation :
The unique substrings are: “a”, “ab”, “b”, “bc”, “c”, “d”, “e”
Hence, the count is 7.
Input : P = “acbacbacaa”, Q = “12300045600078900012345000”, K=2
Output : 3
Explanation :The unique substrings are: “a”, “b”, “aa”
Hence, the count is 3.
Approach:
To solve the above problem, the main idea is to simply iterate through all the substrings and maintain a sum of the weight of all characters encountered so far. If the sum of characters is not greater than K, then insert it in a hashmap otherwise discard it and move forward with another substring. Finally, the result will be the size of the hashmap because it stores all the substring which have weight less than or equal to K.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int distinctSubstring(string& P, string& Q,
int K, int N)
{
unordered_set<string> S;
for (int i = 0; i < N; ++i) {
int sum = 0;
string s;
for (int j = i; j < N; ++j) {
int pos = P[j] - 'a';
sum += Q[pos] - '0';
s += P[j];
if (sum <= K) {
S.insert(s);
}
else {
break;
}
}
}
return S.size();
}
int main()
{
string S = "abcde";
string W = "12345678912345678912345678";
int K = 5;
int N = S.length();
cout << distinctSubstring(S, W, K, N);
return 0;
}
|
Java
import java.io.*;
import java.util.*;
class GFG{
static int distinctSubstring(String P, String Q,
int K, int N)
{
Set<String> S = new HashSet<>();
for(int i = 0; i < N; ++i)
{
int sum = 0;
String s = "";
for(int j = i; j < N; ++j)
{
int pos = P.charAt(j) - 'a';
sum += Q.charAt(pos) - '0';
s += P.charAt(j);
if (sum <= K)
{
S.add(s);
}
else
{
break;
}
}
}
return S.size();
}
public static void main(String args[])
{
String S = "abcde";
String W = "12345678912345678912345678";
int K = 5;
int N = S.length();
System.out.println(distinctSubstring(S, W, K, N));
}
}
|
Python3
def distinctSubstring(P, Q, K, N):
S = set()
for i in range(N):
sum = 0
s = ""
for j in range(i, N):
pos = ord(P[j]) - 97
sum += ord(Q[pos]) - 48
s += P[j]
if (sum <= K):
S.add(s)
else:
break
return len(S)
if __name__ == '__main__':
S = "abcde"
W = "12345678912345678912345678"
K = 5
N = len(S)
print(distinctSubstring(S, W, K, N))
|
C#
using System;
using System.Collections.Generic;
class GFG{
static int distinctSubstring(string P, string Q,
int K, int N)
{
HashSet<string> S = new HashSet<string>();
for(int i = 0; i < N; ++i)
{
int sum = 0;
string s = "";
for(int j = i; j < N; ++j)
{
int pos = P[j] - 'a';
sum += Q[pos] - '0';
s += P[j];
if (sum <= K)
{
S.Add(s);
}
else
{
break;
}
}
}
return S.Count;
}
static void Main()
{
string S = "abcde";
string W = "12345678912345678912345678";
int K = 5;
int N = S.Length;
Console.WriteLine(distinctSubstring(S, W, K, N));
}
}
|
Javascript
<script>
function distinctSubstring(P, Q, K, N)
{
let S = new Set();
for(let i = 0; i < N; ++i)
{
let sum = 0;
let s = "";
for(let j = i; j < N; ++j)
{
let pos = P[j].charCodeAt() - 'a'.charCodeAt();
sum += Q[pos].charCodeAt() - '0'.charCodeAt();
s += P[j];
if (sum <= K)
{
S.add(s);
}
else
{
break;
}
}
}
return S.size;
}
let S = "abcde";
let W = "12345678912345678912345678";
let K = 5;
let N = S.length;
document.write(distinctSubstring(S, W, K, N));
</script>
|
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...