Count numbers whose difference with N is equal to XOR with N
Last Updated :
25 Aug, 2022
Given a number N. The task is to count all possible values of x such that n x is equal to (N-x), where
x is equal to (N-x), where  denotes bitwise XOR operation.
denotes bitwise XOR operation.
Examples:
Input: N = 3
Output: 4
The all possible values of x are respectively 0, 1, 2, 3.
Input: N = 6
Output: 4
The all possible values of x are respectively 0, 2, 4, 6.
Approach: The XOR value of two bits will be 1 if both bits have opposite sign, and 0 when both bits are same. So on the basis of the property of XOR, we can say that n  x is always greater than or equal to n-x. The only condition when its value is equal with n-x is bits of x form a subset of bits of n. Because if in the i’th position both x and n has set bits then after xor the value will decrease, and the decreased value will be
x is always greater than or equal to n-x. The only condition when its value is equal with n-x is bits of x form a subset of bits of n. Because if in the i’th position both x and n has set bits then after xor the value will decrease, and the decreased value will be 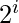 , where i is 0-based position.
, where i is 0-based position.
So the answer is the total count of subsets of bits of number n is 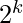 , where k is the count of set bits in n.
, where k is the count of set bits in n.
Below is the implementation of above approach:
C++
#include <bits/stdc++.h>
using namespace std;
void count_values(int n)
{
int set_bits = __builtin_popcount(n);
cout << pow(2, set_bits) << "\n";
}
int main()
{
int n = 27;
count_values(n);
return 0;
}
|
Java
import java.util.*;
class Solution
{
static int __builtin_popcount(int n)
{
int count=0;
while(n>0)
{
if(n%2==1)
count++;
n=n/2;
}
return count;
}
static void count_values(int n)
{
int set_bits = __builtin_popcount(n);
System.out.println((int)Math.pow(2, set_bits));
}
public static void main(String args[])
{
int n = 27;
count_values(n);
}
}
|
Python 3
from math import pow
def __builtin_popcount(n) :
count = 0
while n > 0 :
if n % 2 == 1 :
count += 1
n = n//2
return count
def count_values(n) :
set_bits = __builtin_popcount(n)
print(int(pow(2, set_bits)))
if __name__ == "__main__" :
n = 27
count_values(n)
|
C#
using System;
class GFG
{
static int __builtin_popcount(int n)
{
int count = 0;
while(n > 0)
{
if(n % 2 == 1)
count++;
n = n / 2;
}
return count;
}
static void count_values(int n)
{
int set_bits = __builtin_popcount(n);
Console.Write((int)Math.Pow(2, set_bits));
}
public static void Main()
{
int n = 27;
count_values(n);
}
}
|
PHP
<?php
function __builtin_popcount($n)
{
$count = 0;
while($n > 0)
{
if($n % 2 == 1)
$count++;
$n = $n / 2;
}
return $count;
}
function count_values($n)
{
$set_bits = __builtin_popcount($n);
echo (int)pow(2, $set_bits);
}
$n = 27;
count_values($n);
?>
|
Javascript
<script>
function __builtin_popcount(n)
{
let count = 0;
while(n > 0)
{
if(n % 2 == 1)
count++;
n = parseInt(n / 2);
}
return count;
}
function count_values(n)
{
let set_bits = __builtin_popcount(n);
document.write(Math.pow(2, set_bits) + "<br>");
}
let n = 27;
count_values(n);
</script>
|
Time Complexity: O(k), where k is number of set bits in N.
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...