Count number of triangles possible for the given sides range

Given four integers A, B, C, and D, the task is to find the number of distinct sets (X, Y, and Z) where X, Y and Z denotes the length of sides forming a valid triangle. A ≤ X ≤ B, B ≤ Y ≤ C, and C ≤ Z ≤ D.
Examples:

Input: A = 2, B = 3, C = 4, D = 5 
Output: 7 
Explanation:
Possible Length of Side of Triangles are – 
{(2, 3, 4), (2, 4, 4), (2, 4, 5), (3, 3, 4), (3, 3, 5), (3, 4, 4) and (3, 4, 5)}
Input: A = 1, B = 1, C = 2, D = 2 
Output: 1 
Explanation:
Only possible length of sides we can choose triangle is (1, 2, 2) 

Naive Approach: The key observation in the problem is that, If X, Y and Z are the valid sides of a triangle and X ≤ Y ≤ Z, then sufficient conditions for these sides to form a valid triangle will be X+Y > Z.
Finally, the count of the possible Z value for the given X and Y can be computed as – 

1. If X+Y is greater than D, for this case Z can be chosen from [C, D], Total possible values of Z will be (D-C+1).
2. If X+Y is less than D and greater than C, then Z can be chosen from [C, X+Y-1].
3. If X+Y is less than or equal to C, then we cannot choose Z as these sides will not form a valid triangle.

Time Complexity: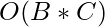

Efficient Approach: The idea is to iterate for all the possible values of A and then compute the number of possible Y and Z values possible for the given X using mathematical computations.
For a given X, the value of X+Y will be in the range of . If we compute the number of possible value greater than D, then the total number of possible values of Y and Z will be – 

// Number of possible values of Y and Z
// If num_greater is the number of possible
// Y values which is greater than D

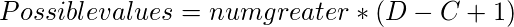
Similarly, Let R and L is the upper bound and Lower Bound of the values of X+Y in the range of C and D. Then, total combinations for Y and Z will be – 

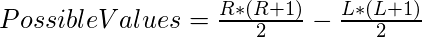
Below is the implementation of the above approach:

C++

// C++ implementation to count the
// number of possible triangles
// for the given sides ranges

#include <bits/stdc++.h>
using namespace std;

// Function to count the number of
// possible triangles for the given
// sides ranges
int count_triangles(int a, int b,
                    int c, int d)
{

    int ans = 0;

    // Iterate for every possible of x
    for (int x = a; x <= b; ++x) {

        // Range of y is [b, c]
        // From this range First
        // we will find the number
        // of x + y greater than d
        int num_greater_than_d = max(d, c + x) - max(d, b + x - 1);

        // For x+y greater than d
        // we can choose all z from [c, d]
        // Total permutation will be
        ans += num_greater_than_d * (d - c + 1);

        // Now we will find the number
        // of x+y in between the [c, d]
        int r = min(max(c, c + x), d) - c;
        int l = min(max(c, b + x - 1), d) - c;

        // [l, r] will be the range
        // from total [c, d] x+y belongs
        // For any r such that r = x+y
        // We can choose z, in the range
        // [c, d] only less than r,
        // Thus total permutation be
        int x1 = (r * (r + 1)) / 2;
        int x2 = (l * (l + 1)) / 2;

        ans += x1 - x2;
    }

    return ans;
}

// Driver Code
int main()
{
    int a = 2, b = 3, c = 4, d = 5;

    cout << count_triangles(a, b, c, d)
         << endl;

    return 0;
}

Java

// Java implementation to count the
// number of possible triangles
// for the given sides ranges
import java.util.Scanner;
import java.util.Arrays;

class GFG{

// Function to count the number of
// possible triangles for the given
// sides ranges
public static int count_triangles(int a, int b,
                                  int c, int d)
{
    int ans = 0;

    // Iterate for every possible of x
    for(int x = a; x <= b; ++x)
    {

        // Range of y is [b, c]
        // From this range First
        // we will find the number
        // of x + y greater than d
        int num_greater_than_d = Math.max(d, c + x) -
                                 Math.max(d, b + x - 1);

        // For x+y greater than d
        // we can choose all z from [c, d]
        // Total permutation will be
        ans += num_greater_than_d * (d - c + 1);

        // Now we will find the number
        // of x+y in between the [c, d]
        int r = Math.min(Math.max(c, c + x), d) - c;
        int l = Math.min(Math.max(c, b + x - 1), d) - c;

        // [l, r] will be the range
        // from total [c, d] x+y belongs
        // For any r such that r = x+y
        // We can choose z, in the range
        // [c, d] only less than r,
        // Thus total permutation be
        int x1 = (r * (r + 1)) / 2;
        int x2 = (l * (l + 1)) / 2;

        ans += x1 - x2;
    }
    return ans;
}

// Driver Code
public static void main(String args[])
{
    int a = 2, b = 3, c = 4, d = 5;

    System.out.println(count_triangles(a, b, c, d));
}
}

// This code is contributed by SoumikMondal

Python3

# Python3 implementation to count
# the number of possible triangles
# for the given sides ranges

# Function to count the number of
# possible triangles for the given
# sides ranges
def count_triangles(a, b, c, d):

    ans = 0

    # Iterate for every possible of x
    for x in range(a, b + 1):

        # Range of y is [b, c]
        # From this range First
        # we will find the number
        # of x + y greater than d
        num_greater_than_d = (max(d, c + x) -
                              max(d, b + x - 1))

        # For x+y greater than d we
        # can choose all z from [c, d]
        # Total permutation will be
        ans = (ans + num_greater_than_d *
                             (d - c + 1))

        # Now we will find the number
        # of x+y in between the [c, d]
        r = min(max(c, c + x), d) - c;
        l = min(max(c, b + x - 1), d) - c;

        # [l, r] will be the range
        # from total [c, d] x+y belongs
        # For any r such that r = x+y
        # We can choose z, in the range
        # [c, d] only less than r,
        # Thus total permutation be
        x1 = int((r * (r + 1)) / 2)
        x2 = int((l * (l + 1)) / 2)

        ans = ans + (x1 - x2)

    return ans

# Driver Code
a = 2
b = 3
c = 4
d = 5

print (count_triangles(a, b, c, d), end = '\n')

# This code is contributed by PratikBasu

C#

// C# implementation to count the
// number of possible triangles
// for the given sides ranges
using System;

class GFG{

// Function to count the number of
// possible triangles for the given
// sides ranges
public static int count_triangles(int a, int b,
                                  int c, int d)
{
    int ans = 0;

    // Iterate for every possible of x
    for(int x = a; x <= b; ++x)
    {

        // Range of y is [b, c]
        // From this range First
        // we will find the number
        // of x + y greater than d
        int num_greater_than_d = Math.Max(d, c + x) -
                                 Math.Max(d, b + x - 1);

        // For x+y greater than d
        // we can choose all z from [c, d]
        // Total permutation will be
        ans += num_greater_than_d * (d - c + 1);

        // Now we will find the number
        // of x+y in between the [c, d]
        int r = Math.Min(Math.Max(c, c + x), d) - c;
        int l = Math.Min(Math.Max(c, b + x - 1), d) - c;

        // [l, r] will be the range
        // from total [c, d] x+y belongs
        // For any r such that r = x+y
        // We can choose z, in the range
        // [c, d] only less than r,
        // Thus total permutation be
        int x1 = (r * (r + 1)) / 2;
        int x2 = (l * (l + 1)) / 2;

        ans += x1 - x2;
    }
    return ans;
}

// Driver Code
public static void Main(String []args)
{
    int a = 2, b = 3, c = 4, d = 5;

    Console.WriteLine(count_triangles(a, b, c, d));
}
}

// This code is contributed by gauravrajput1

Javascript

<script>

// JavaScript implementation to count the
// number of possible triangles
// for the given sides ranges

// Function to count the number of
// possible triangles for the given
// sides ranges
function count_triangles(a , b, c , d)
{
    var ans = 0;

    // Iterate for every possible of x
    for(x = a; x <= b; ++x)
    {

        // Range of y is [b, c]
        // From this range First
        // we will find the number
        // of x + y greater than d
        var num_greater_than_d = Math.max(d, c + x) -
                                 Math.max(d, b + x - 1);

        // For x+y greater than d
        // we can choose all z from [c, d]
        // Total permutation will be
        ans += num_greater_than_d * (d - c + 1);

        // Now we will find the number
        // of x+y in between the [c, d]
        var r = Math.min(Math.max(c, c + x), d) - c;
        var l = Math.min(Math.max(c, b + x - 1), d) - c;

        // [l, r] will be the range
        // from total [c, d] x+y belongs
        // For any r such that r = x+y
        // We can choose z, in the range
        // [c, d] only less than r,
        // Thus total permutation be
        var x1 = (r * (r + 1)) / 2;
        var x2 = (l * (l + 1)) / 2;

        ans += x1 - x2;
    }
    return ans;
}

// Driver Code

var a = 2, b = 3, c = 4, d = 5;

document.write(count_triangles(a, b, c, d));

// This code contributed by shikhasingrajput

</script>

Output:

7

Time Complexity : O(b-a)

Space Complexity : O(1) ,as we are not using any extra space