Count number of triangles possible for the given sides range
Last Updated :
15 Jun, 2022
Given four integers A, B, C, and D, the task is to find the number of distinct sets (X, Y, and Z) where X, Y and Z denotes the length of sides forming a valid triangle. A ? X ? B, B ? Y ? C, and C ? Z ? D.
Examples:
Input: A = 2, B = 3, C = 4, D = 5
Output: 7
Explanation:
Possible Length of Side of Triangles are –
{(2, 3, 4), (2, 4, 4), (2, 4, 5), (3, 3, 4), (3, 3, 5), (3, 4, 4) and (3, 4, 5)}
Input: A = 1, B = 1, C = 2, D = 2
Output: 1
Explanation:
Only possible length of sides we can choose triangle is (1, 2, 2)
Naive Approach: The key observation in the problem is that, If X, Y and Z are the valid sides of a triangle and X ? Y ? Z, then sufficient conditions for these sides to form a valid triangle will be X+Y > Z.
Finally, the count of the possible Z value for the given X and Y can be computed as –
- If X+Y is greater than D, for this case Z can be chosen from [C, D], Total possible values of Z will be (D-C+1).
- If X+Y is less than D and greater than C, then Z can be chosen from [C, X+Y-1].
- If X+Y is less than or equal to C, then we cannot choose Z as these sides will not form a valid triangle.
Time Complexity: 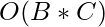
Efficient Approach: The idea is to iterate for all the possible values of A and then compute the number of possible Y and Z values possible for the given X using mathematical computations.
For a given X, the value of X+Y will be in the range of ![Rendered by QuickLaTeX.com [X+B, X+C]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6445e5e43500cea90532bfc63e2e3267_l3.png) . If we compute the number of possible value greater than D, then the total number of possible values of Y and Z will be –
. If we compute the number of possible value greater than D, then the total number of possible values of Y and Z will be –
// Number of possible values of Y and Z
// If num_greater is the number of possible
// Y values which is greater than D
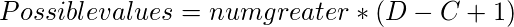
Similarly, Let R and L is the upper bound and Lower Bound of the values of X+Y in the range of C and D. Then, total combinations for Y and Z will be –
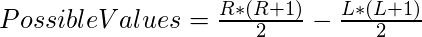
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int count_triangles(int a, int b,
int c, int d)
{
int ans = 0;
for (int x = a; x <= b; ++x) {
int num_greater_than_d = max(d, c + x) - max(d, b + x - 1);
ans += num_greater_than_d * (d - c + 1);
int r = min(max(c, c + x), d) - c;
int l = min(max(c, b + x - 1), d) - c;
int x1 = (r * (r + 1)) / 2;
int x2 = (l * (l + 1)) / 2;
ans += x1 - x2;
}
return ans;
}
int main()
{
int a = 2, b = 3, c = 4, d = 5;
cout << count_triangles(a, b, c, d)
<< endl;
return 0;
}
|
Java
import java.util.Scanner;
import java.util.Arrays;
class GFG{
public static int count_triangles(int a, int b,
int c, int d)
{
int ans = 0;
for(int x = a; x <= b; ++x)
{
int num_greater_than_d = Math.max(d, c + x) -
Math.max(d, b + x - 1);
ans += num_greater_than_d * (d - c + 1);
int r = Math.min(Math.max(c, c + x), d) - c;
int l = Math.min(Math.max(c, b + x - 1), d) - c;
int x1 = (r * (r + 1)) / 2;
int x2 = (l * (l + 1)) / 2;
ans += x1 - x2;
}
return ans;
}
public static void main(String args[])
{
int a = 2, b = 3, c = 4, d = 5;
System.out.println(count_triangles(a, b, c, d));
}
}
|
Python3
def count_triangles(a, b, c, d):
ans = 0
for x in range(a, b + 1):
num_greater_than_d = (max(d, c + x) -
max(d, b + x - 1))
ans = (ans + num_greater_than_d *
(d - c + 1))
r = min(max(c, c + x), d) - c;
l = min(max(c, b + x - 1), d) - c;
x1 = int((r * (r + 1)) / 2)
x2 = int((l * (l + 1)) / 2)
ans = ans + (x1 - x2)
return ans
a = 2
b = 3
c = 4
d = 5
print (count_triangles(a, b, c, d), end = '\n')
|
C#
using System;
class GFG{
public static int count_triangles(int a, int b,
int c, int d)
{
int ans = 0;
for(int x = a; x <= b; ++x)
{
int num_greater_than_d = Math.Max(d, c + x) -
Math.Max(d, b + x - 1);
ans += num_greater_than_d * (d - c + 1);
int r = Math.Min(Math.Max(c, c + x), d) - c;
int l = Math.Min(Math.Max(c, b + x - 1), d) - c;
int x1 = (r * (r + 1)) / 2;
int x2 = (l * (l + 1)) / 2;
ans += x1 - x2;
}
return ans;
}
public static void Main(String []args)
{
int a = 2, b = 3, c = 4, d = 5;
Console.WriteLine(count_triangles(a, b, c, d));
}
}
|
Javascript
<script>
function count_triangles(a , b, c , d)
{
var ans = 0;
for(x = a; x <= b; ++x)
{
var num_greater_than_d = Math.max(d, c + x) -
Math.max(d, b + x - 1);
ans += num_greater_than_d * (d - c + 1);
var r = Math.min(Math.max(c, c + x), d) - c;
var l = Math.min(Math.max(c, b + x - 1), d) - c;
var x1 = (r * (r + 1)) / 2;
var x2 = (l * (l + 1)) / 2;
ans += x1 - x2;
}
return ans;
}
var a = 2, b = 3, c = 4, d = 5;
document.write(count_triangles(a, b, c, d));
</script>
|
Time Complexity : O(b-a)
Space Complexity : O(1) ,as we are not using any extra space
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...