Count number of paths whose weight is exactly X and has at-least one edge of weight M

Given an infinite tree and three numbers N, M, and X which has exactly N child from every node. Every edge has a weight of 1, 2, 3, 4..N. The task is to find the count of paths whose weight is exactly X and has a minimum of one edge of weight M in it. 

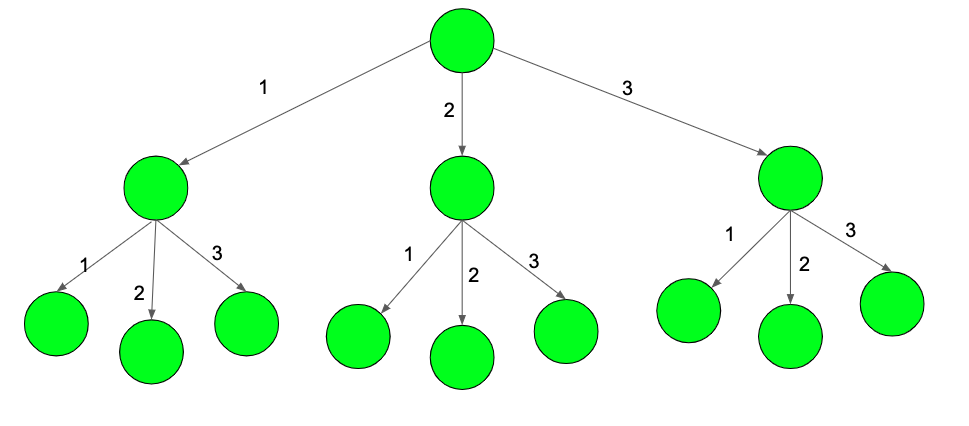
The diagram above shows a tree shown till level-3 and N = 3. 

Examples:

Input: N = 3, M = 2, X = 3
Output: 2
The path 1-2 and 2-1 in the image above 

Input:  N = 2, M = 1, X = 4
Output:  4 

Approach: The problem can be solved using Dynamic Programming and memoization. We will use a top-down approach to solve this problem. Recur starting from the root with the sum initially as X, and recursively traverse all paths possible( which is from 1 to N). If the node is equal to M, then the second parameter becomes true, else it stays the same which has been passed in the previous call. Store the value in a DP[][] table to avoid visiting the same states twice. 

Below is the implementation of the above approach.  

C++

// C++ program to count the number of paths
#include <bits/stdc++.h>
using namespace std;
#define max 4
#define c 2

// Function to find the number of paths
int countPaths(int sum, int get, int m, int n, int dp[])
{

    // If the summation is more than X
    if (sum < 0)
        return 0;

    // If exactly X weights have reached
    if (sum == 0)
        return get;

    // Already visited
    if (dp[sum][get] != -1)
        return dp[sum][get];

    // Count paths
    int res = 0;

    // Traverse in all paths
    for (int i = 1; i <= n; i++) {

        // If the edge weight is M
        if (i == m)
            res += countPaths(sum - i, 1, m, n, dp);
        else // Edge's weight is not M
            res += countPaths(sum - i, get, m, n, dp);
    }

    dp[sum][get] = res;

    return dp[sum][get];
}

// Driver Code
int main()
{
    int n = 3, m = 2, x = 3;

    int dp[max + 1];

    // Initialized the DP array with -1
    for (int i = 0; i <= max; i++)
        for (int j = 0; j < 2; j++)
            dp[i][j] = -1;

    // Function to count paths
    cout << countPaths(x, 0, m, n, dp);
}

Java

// Java program to count the number of paths

public class GFG{

    static int max = 4 ;
    static int  c = 2 ;

    // Function to find the number of paths
    static int countPaths(int sum, int get, int m, int n, int dp[][])
    {

        // If the summation is more than X
        if (sum < 0)
            return 0;

        // If exactly X weights have reached
        if (sum == 0)
            return get;

        // Already visited
        if (dp[sum][get] != -1)
            return dp[sum][get];

        // Count paths
        int res = 0;

        // Traverse in all paths
        for (int i = 1; i <= n; i++) {

            // If the edge weight is M
            if (i == m)
                res += countPaths(sum - i, 1, m, n, dp);
            else // Edge's weight is not M
                res += countPaths(sum - i, get, m, n, dp);
        }

        dp[sum][get] = res;

        return dp[sum][get];
    }

    // Driver Code
    public static void main(String []args)
    {
        int n = 3, m = 2, x = 3;

        int dp[][] = new int[max + 1][2];

        // Initialized the DP array with -1
        for (int i = 0; i <= max; i++)
            for (int j = 0; j < 2; j++)
                dp[i][j] = -1;

        // Function to count paths
        System.out.println(countPaths(x, 0, m, n, dp));
    }
    // This code is contributed by Ryuga
}

Python3

# Python3 program to count the number of paths
Max = 4
c = 2

# Function to find the number of paths
def countPaths(Sum, get, m, n, dp):

    # If the Summation is more than X
    if (Sum < 0):
        return 0

    # If exactly X weights have reached
    if (Sum == 0):
        return get

    # Already visited
    if (dp[Sum][get] != -1):
        return dp[Sum][get]

    # Count paths
    res = 0

    # Traverse in all paths
    for i in range(1, n + 1):

        # If the edge weight is M
        if (i == m):
            res += countPaths(Sum - i, 1, m, n, dp)
        else: # Edge's weight is not M
            res += countPaths(Sum - i, get, m, n, dp)

    dp[Sum][get] = res

    return dp[Sum][get]

# Driver Code
n = 3
m = 2
x = 3
dp = [[-1 for i in range(2)]
          for i in range(Max + 1)]

# Initialized the DP array with -1
for i in range(Max + 1):
    for j in range(2):
        dp[i][j] = -1

# Function to count paths
print(countPaths(x, 0, m, n, dp))

# This code is contributed by Mohit kumar 29

C#

// C# program to count the number of paths
using System;

class GFG
{
    static int max = 4 ;
    static int c = 2 ;

    // Function to find the number of paths
    static int countPaths(int sum, int get, int m,
                          int n, int[, ] dp)
    {

        // If the summation is more than X
        if (sum < 0)
            return 0;

        // If exactly X weights have reached
        if (sum == 0)
            return get;

        // Already visited
        if (dp[sum, get] != -1)
            return dp[sum, get];

        // Count paths
        int res = 0;

        // Traverse in all paths
        for (int i = 1; i <= n; i++)
        {

            // If the edge weight is M
            if (i == m)
                res += countPaths(sum - i, 1, m, n, dp);
            else // Edge's weight is not M
                res += countPaths(sum - i, get, m, n, dp);
        }

        dp[sum, get] = res;

        return dp[sum, get];
    }

    // Driver Code
    public static void Main()
    {
        int n = 3, m = 2, x = 3;

        int[,] dp = new int[max + 1, 2];

        // Initialized the DP array with -1
        for (int i = 0; i <= max; i++)
            for (int j = 0; j < 2; j++)
                dp[i, j] = -1;

        // Function to count paths
        Console.WriteLine(countPaths(x, 0, m, n, dp));
    }
}

// This code is contributed by Akanksha Rai

PHP

<?php

// PHP program to count the number of paths

$max = 4;
$c = 2;

// Function to find the number of paths
function countPaths($sum, $get, $m, $n, &$dp)
{
    global $max,$c;
    // If the summation is more than X
    if ($sum < 0)
        return 0;

    // If exactly X weights have reached
    if ($sum == 0)
        return $get;

    // Already visited
    if ($dp[$sum][$get] != -1)
        return $dp[$sum][$get];

    // Count paths
    $res = 0;

    // Traverse in all paths
    for ($i = 1; $i <= $n; $i++)
    {

        // If the edge weight is M
        if ($i == $m)
            $res += countPaths($sum - $i, 1, $m, $n, $dp);
        else // Edge's weight is not M
            $res += countPaths($sum - $i, $get, $m, $n, $dp);
    }

    $dp[$sum][$get] = $res;

    return $dp[$sum][$get];
}

// Driver Code

    $n = 3;
    $m = 2;
    $x = 3;

    $dp = array_fill(0,$max + 1,NULL);

    // Initialized the DP array with -1
    for ($i = 0; $i <= $max; $i++)
        for ($j = 0; $j < 2; $j++)
            $dp[$i][$j] = -1;

    // Function to count paths
    echo countPaths($x, 0, $m, $n, $dp);

    // This code is contributed by ChitraNayal
?>

Javascript

<script>

// Javascript program to count the number of paths
let max = 4;
let c = 2;

// Function to find the number of paths
function countPaths(sum, get, m, n, dp)
{

    // If the summation is more than X
    if (sum < 0)
        return 0;

    // If exactly X weights have reached
    if (sum == 0)
        return get;

    // Already visited
    if (dp[sum][get] != -1)
        return dp[sum][get];

    // Count paths
    let res = 0;

    // Traverse in all paths
    for(let i = 1; i <= n; i++)
    {

        // If the edge weight is M
        if (i == m)
            res += countPaths(sum - i, 1,
                              m, n, dp);

        // Edge's weight is not M
        else
            res += countPaths(sum - i, get,
                              m, n, dp);
    }
    dp[sum][get] = res;

    return dp[sum][get];
}

// Driver Code
let  n = 3, m = 2, x = 3;
let dp = new Array(max + 1);

// Initialized the DP array with -1
for(let i = 0; i <= max; i++)
{
    dp[i] = new Array(2)
    for(let j = 0; j < 2; j++)
        dp[i][j] = -1;
}

// Function to count paths
document.write(countPaths(x, 0, m, n, dp));

// This code is contributed by avanitrachhadiya2155

</script>

Output

2

Complexity Analysis:

• Time Complexity: O(x*n), as we are using a loop to traverse n times and in each traversal, we are recursively calling the function again which will cost O(x). Where n is the number of children from every node and x is the total weight.
• Auxiliary Space: O(x*n), as we are using extra space for the DP matrix. Where n is the number of children from every node and x is the total weight.