Count distinct occurrences as a subsequence

Given a two strings S and T, find the count of distinct occurrences of T in S as a subsequence.
Examples:

Input: S = banana, T = ban
Output: 3
Explanation: T appears in S as below three subsequences.
[ban], [ba  n], [b   an]

Input: S = geeksforgeeks, T = ge
Output: 6
Explanation: T appears in S as below six subsequences.
[ge], [     ge], [g e], [g    e] [g     e]
and [     g e]      

Approach: Create a recursive function such that it returns count of subsequences of S that match T. Here m is the length of T and n is length of S. This problem can be recursively defined as below. 

1. Given the string T is an empty string, returning 1 as an empty string can be the subsequence of all.
2. Given the string S is an empty string, returning 0 as no string can be the subsequence of an empty string.
3. If the last character of S and T do not match, then remove the last character of S and call the recursive function again. Because the last character of S cannot be a part of the subsequence or remove it and check for other characters.
4. If the last character of S match then there can be two possibilities, first there can be a subsequence where the last character of S is a part of it and second where it is not a part of the subsequence. So the required value will be the sum of both. Call the recursive function once with last character of both the strings removed and again with only last character of S removed.
   

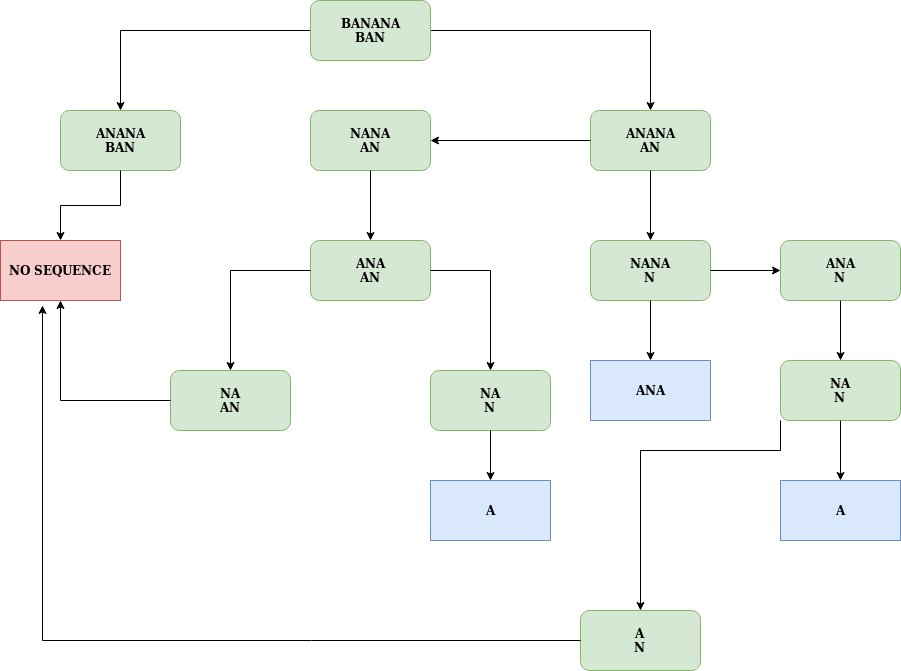
Blue round rectangles represent accepted states or there are a subsequence and red round rectangles represent No subsequence can be formed.

Implementation  of Recursive Approach:

C++

/* C/C++ program to count number of times S appears
   as a subsequence in T */
#include <bits/stdc++.h>
using namespace std;

int f(int i, int j, string s, string t)
{
    if (j >= t.size()) {
        return 1;
    }

    if (i >= s.size()) {
        return 0;
    }

    if (s[i] == t[j]) {
        return f(i + 1, j + 1, s, t) + f(i + 1, j, s, t);
    }

    return f(i + 1, j, s, t);
}

int findSubsequenceCount(string s, string t)
{
    return f(0, 0, s, t);
}

// Driver code to check above method
int main()
{
    string T = "ge";
    string S = "geeksforgeeks";
    cout << findSubsequenceCount(S, T) << endl;
    return 0;
}

Java

// Java program to count number of times
// S appears as a subsequence in T
import java.io.*;

class GFG {
    static int f(int i, int j, String s,
                                    String t)
    {
        // base case
        // if second string completed then we found the
        // matching pattern
        if (j >= t.length()) {
            return 1;
        }
        // if first string is completed we can not find any
        // matching pattern.
        if (i >= s.length()) {
            return 0;
        }
        // if character at i'th place is equal to character
        // at j'th place then
        // we can either take it or not take it.
        if (s.charAt(i) == t.charAt(j)) {
            return f(i + 1, j + 1, s, t)
                + f(i + 1, j, s, t);
        }
        // if characters are not equal then we will increase
        // only first string
        return f(i + 1, j, s, t);
    }

    // Driver code to check above method
    public static void main(String[] args)
    {
        String T = "ge";
        String S = "geeksforgeeks";
        System.out.println(
            f(0, 0, S, T));
    }
}
// This code is contributed by Sanskar.

Python3

# Python program to count number of times S appears
# as a subsequence in T
def f(i, j, s, t):

  # base case
       # if second string completed then we found the
        # matching pattern
    if(j >= len(t)):
        return 1

      # if first string is completed we can not find any
      #  matching pattern.
    if(i >= len(s)):
        return 0

      # if character at i'th place is equal to character
      # at j'th place then
      # we can either take it or not take it.
    if(s[i] == t[j]):
        return f(i + 1, j + 1, s, t) + f(i + 1, j, s, t)

      # if characters are not equal then we will increase
      # only first string
    return f(i + 1, j, s, t)

def findSubsequenceCount(s, t):
    return f(0, 0, s, t)

# Driver code to check above method
T = "ge"
S = "geeksforgeeks"
print(findSubsequenceCount(S,T))

# This code is contributed by Aman Kumar.

C#

// C# program to count number of times S appears
//as a subsequence in T
using System;

class GFG {

    static int f(int i, int j, string s, string t)
    {
        // base case
        // if second string completed then we found the
        // matching pattern
        if (j >= t.Length) {
            return 1;
        }

        // if first string is completed we can not find any
        // matching pattern.
        if (i >= s.Length) {
            return 0;
        }

        // if character at i'th place is equal to character
        // at j'th place then
        // we can either take it or not take it.
        if (s[i] == t[j])
        return f(i + 1, j + 1, s, t) + f(i + 1, j, s, t);

      // if characters are not equal then we will increase
      // only first string
      return f(i + 1, j, s, t);

    }


    static int findSubsequenceCount(string s, string t)
    {
        return f(0, 0, s, t);
    }

    // Driver code to check above method
    public static void Main()
    {
        string T = "ge";
        string S = "geeksforgeeks";
        Console.WriteLine(findSubsequenceCount(S, T));
    }
}

Javascript

<script>
// Javascript program to count number of times S appears
// as a subsequence in T


function f(i, j, s, t) {
  if (j >= t.length) {
    return 1;
  }

  if (i >= s.length) {
    return 0;
  }

  if (s[i] == t[j]) {
    return f(i + 1, j + 1, s, t) + f(i + 1, j, s, t);
  }

  return f(i + 1, j, s, t);
}

function findSubsequenceCount(s, t) {
  return f(0, 0, s, t);
}

// Driver code to check above method

let T = "ge";
let S = "geeksforgeeks";
document.write(findSubsequenceCount(S, T))
</script>

Output

6

Since there are overlapping subproblems in the above recurrence result, Dynamic Programming approach can be applied to solve the above problem. Store the subproblems in a Hashmap or an array and return the value when the function is called again.

Algorithm:

1. Create a 2D array mat[m+1][n+1] where m is length of string T and n is length of string S. mat[i][j] denotes the number of distinct subsequence of substring S(1..i) and substring T(1..j) so mat[m][n] contains our solution. 
2. Initialize the first column with all 0s. An empty string can’t have another string as subsequence
3. Initialize the first row with all 1s. An empty string is a subsequence of all.
4. Fill the matrix in bottom-up manner, i.e. all the sub problems of the current string is calculated first.
5. Traverse the string T from start to end. (counter is i)
6. For every iteration of the outer loop, Traverse the string S from start to end. (counter is j)
7. If the character at ith index of string T matches with jth character of string S, the value is obtained considering two cases. First, is all the substrings without last character in S and second is the substrings without last characters in both, i.e mat[i+1][j] + mat[i][j] .
8. Else the value will be same even if jth character of S is removed, i.e. mat[i+1][j]
9. Print the value of mat[m][n] as the answer. 

C++

/* C/C++ program to count number of times S appears
   as a subsequence in T */
#include <bits/stdc++.h>
using namespace std;

int findSubsequenceCount(string S, string T)
{
    int m = T.length(), n = S.length();

    // T can't appear as a subsequence in S
    if (m > n)
        return 0;

    // mat[i][j] stores the count of occurrences of
    // T(1..i) in S(1..j).
    int mat[m + 1][n + 1];

    // Initializing first column with all 0s. An empty
    // string can't have another string as subsequence
    for (int i = 1; i <= m; i++)
        mat[i][0] = 0;

    // Initializing first row with all 1s. An empty
    // string is subsequence of all.
    for (int j = 0; j <= n; j++)
        mat[0][j] = 1;

    // Fill mat[][] in bottom up manner
    for (int i = 1; i <= m; i++) {
        for (int j = 1; j <= n; j++) {

            // If last characters don't match, then value
            // is same as the value without last character
            // in S.
            if (T[i - 1] != S[j - 1])
                mat[i][j] = mat[i][j - 1];

            // Else value is obtained considering two cases.
            // a) All substrings without last character in S
            // b) All substrings without last characters in
            // both.
            else
                mat[i][j] = mat[i][j - 1] + mat[i - 1][j - 1];
        }
    }

    /* uncomment this to print matrix mat
    for (int i = 1; i <= m; i++, cout << endl)
        for (int j = 1; j <= n; j++)
            cout << mat[i][j] << " ";  */
    return mat[m][n];
}

// Driver code to check above method
int main()
{
    string T = "ge";
    string S = "geeksforgeeks";
    cout << findSubsequenceCount(S, T) << endl;
    return 0;
}

Java

// Java program to count number of times
// S appears as a subsequence in T
import java.io.*;

class GFG {
    static int findSubsequenceCount(String S, String T)
    {
        int m = T.length();
        int n = S.length();

        // T can't appear as a subsequence in S
        if (m > n)
            return 0;

        // mat[i][j] stores the count of
        // occurrences of T(1..i) in S(1..j).
        int mat[][] = new int[m + 1][n + 1];

        // Initializing first column with
        // all 0s. An emptystring can't have
        // another string as subsequence
        for (int i = 1; i <= m; i++)
            mat[i][0] = 0;

        // Initializing first row with all 1s.
        // An empty string is subsequence of all.
        for (int j = 0; j <= n; j++)
            mat[0][j] = 1;

        // Fill mat[][] in bottom up manner
        for (int i = 1; i <= m; i++) {
            for (int j = 1; j <= n; j++) {
                // If last characters don't match,
                // then value is same as the value
                // without last character in S.
                if (T.charAt(i - 1) != S.charAt(j - 1))
                    mat[i][j] = mat[i][j - 1];

                // Else value is obtained considering two cases.
                // a) All substrings without last character in S
                // b) All substrings without last characters in
                // both.
                else
                    mat[i][j] = mat[i][j - 1] + mat[i - 1][j - 1];
            }
        }

        /* uncomment this to print matrix mat
        for (int i = 1; i <= m; i++, cout << endl)
            for (int j = 1; j <= n; j++)
                System.out.println ( mat[i][j] +" "); */
        return mat[m][n];
    }

    // Driver code to check above method
    public static void main(String[] args)
    {
        String T = "ge";
        String S = "geeksforgeeks";
        System.out.println(findSubsequenceCount(S, T));
    }
}
// This code is contributed by vt_m

Python3

# Python3 program to count number of times
# S appears as a subsequence in T
def findSubsequenceCount(S, T):

    m = len(T)
    n = len(S)

    # T can't appear as a subsequence in S
    if m > n:
        return 0

    # mat[i][j] stores the count of
    # occurrences of T(1..i) in S(1..j).
    mat = [[0 for _ in range(n + 1)]
              for __ in range(m + 1)]

    # Initializing first column with all 0s. x
    # An empty string can't have another
    # string as subsequence
    for i in range(1, m + 1):
        mat[i][0] = 0

    # Initializing first row with all 1s.
    # An empty string is subsequence of all.
    for j in range(n + 1):
        mat[0][j] = 1

    # Fill mat[][] in bottom up manner
    for i in range(1, m + 1):
        for j in range(1, n + 1):

            # If last characters don't match,
            # then value is same as the value
            # without last character in S.
            if T[i - 1] != S[j - 1]:
                mat[i][j] = mat[i][j - 1]

            # Else value is obtained considering two cases.
            # a) All substrings without last character in S
            # b) All substrings without last characters in
            # both.
            else:
                mat[i][j] = (mat[i][j - 1] +
                             mat[i - 1][j - 1])

    return mat[m][n]

# Driver Code
if __name__ == "__main__":
    T = "ge"
    S = "geeksforgeeks"
    print(findSubsequenceCount(S, T))

# This code is contributed
# by vibhu4agarwal

C#

// C# program to count number of times
// S appears as a subsequence in T
using System;

class GFG {

    static int findSubsequenceCount(string S, string T)
    {
        int m = T.Length;
        int n = S.Length;

        // T can't appear as a subsequence in S
        if (m > n)
            return 0;

        // mat[i][j] stores the count of
        // occurrences of T(1..i) in S(1..j).
        int[, ] mat = new int[m + 1, n + 1];

        // Initializing first column with
        // all 0s. An emptystring can't have
        // another string as subsequence
        for (int i = 1; i <= m; i++)
            mat[i, 0] = 0;

        // Initializing first row with all 1s.
        // An empty string is subsequence of all.
        for (int j = 0; j <= n; j++)
            mat[0, j] = 1;

        // Fill mat[][] in bottom up manner
        for (int i = 1; i <= m; i++) {

            for (int j = 1; j <= n; j++) {

                // If last characters don't match,
                // then value is same as the value
                // without last character in S.
                if (T[i - 1] != S[j - 1])
                    mat[i, j] = mat[i, j - 1];

                // Else value is obtained considering two cases.
                // a) All substrings without last character in S
                // b) All substrings without last characters in
                // both.
                else
                    mat[i, j] = mat[i, j - 1] + mat[i - 1, j - 1];
            }
        }

        /* uncomment this to print matrix mat
        for (int i = 1; i <= m; i++, cout << endl)
            for (int j = 1; j <= n; j++)
                System.out.println ( mat[i][j] +" "); */
        return mat[m, n];
    }

    // Driver code to check above method
    public static void Main()
    {
        string T = "ge";
        string S = "geeksforgeeks";
        Console.WriteLine(findSubsequenceCount(S, T));
    }
}

// This code is contributed by vt_m

PHP

<?php
// PHP program to count number of times
// S appears as a subsequence in T */

function findSubsequenceCount($S, $T)
{
    $m = strlen($T); $n = strlen($S);

    // T can't appear as a subsequence in S
    if ($m > $n)
        return 0;

    // mat[i][j] stores the count of
    // occurrences of T(1..i) in S(1..j).
    $mat = array(array());

    // Initializing first column with all 0s.
    // An empty string can't have another
    // string as subsequence
    for ($i = 1; $i <= $m; $i++)
        $mat[$i][0] = 0;

    // Initializing first row with all 1s.
    // An empty string is subsequence of all.
    for ($j = 0; $j <= $n; $j++)
        $mat[0][$j] = 1;

    // Fill mat[][] in bottom up manner
    for ($i = 1; $i <= $m; $i++)
    {
        for ($j = 1; $j <= $n; $j++)
        {
            // If last characters don't match,
            // then value is same as the value
            // without last character in S.
            if ($T[$i - 1] != $S[$j - 1])
                $mat[$i][$j] = $mat[$i][$j - 1];

            // Else value is obtained considering two cases.
            // a) All substrings without last character in S
            // b) All substrings without last characters in
            // both.
            else
                $mat[$i][$j] = $mat[$i][$j - 1] +
                               $mat[$i - 1][$j - 1];
        }
    }

    /* uncomment this to print matrix mat
    for (int i = 1; i <= m; i++, cout << endl)
        for (int j = 1; j <= n; j++)
            cout << mat[i][j] << " "; */
    return $mat[$m][$n];
}

// Driver Code
$T = "ge";
$S = "geeksforgeeks";
echo findSubsequenceCount($S, $T) . "\n";

// This code is contributed
// by Akanksha Rai

Javascript

<script>

    // JavaScript program to count number of times
    // S appears as a subsequence in T

    function findSubsequenceCount(S, T)
    {
        let m = T.length;
        let n = S.length;

        // T can't appear as a subsequence in S
        if (m > n)
            return 0;

        // mat[i][j] stores the count of
        // occurrences of T(1..i) in S(1..j).
        let mat = new Array(m + 1);
        for (let i = 0; i <= m; i++)
        {
            mat[i] = new Array(n + 1);
            for (let j = 0; j <= n; j++)
            {
                mat[i][j] = 0;
            }
        }

        // Initializing first column with
        // all 0s. An emptystring can't have
        // another string as subsequence
        for (let i = 1; i <= m; i++)
            mat[i][0] = 0;

        // Initializing first row with all 1s.
        // An empty string is subsequence of all.
        for (let j = 0; j <= n; j++)
            mat[0][j] = 1;

        // Fill mat[][] in bottom up manner
        for (let i = 1; i <= m; i++) {
            for (let j = 1; j <= n; j++) {
                // If last characters don't match,
                // then value is same as the value
                // without last character in S.
                if (T[i - 1] != S[j - 1])
                    mat[i][j] = mat[i][j - 1];

                // Else value is obtained
                // considering two cases.
                // a) All substrings without
                // last character in S
                // b) All substrings without
                // last characters in
                // both.
                else
                    mat[i][j] = mat[i][j - 1] +
                    mat[i - 1][j - 1];
            }
        }

        /* uncomment this to print matrix mat
        for (int i = 1; i <= m; i++, cout << endl)
            for (int j = 1; j <= n; j++)
                System.out.println ( mat[i][j] +" "); */
        return mat[m][n];
    }

    let T = "ge";
    let S = "geeksforgeeks";
    document.write(findSubsequenceCount(S, T));

</script>

Output

6

Complexity Analysis:

• Time Complexity: O(m*n). 
  Only one traversal of the matrix is needed, so the time Complexity is O(m*n)
• Auxiliary Space: O(m*n). 
  A matrix of size m*n is needed so the space complexity is O(m*n). 
  Note:Since mat[i][j] accesses elements of the current row and previous row only, we can optimize auxiliary space just by using two rows only reducing space from m*n to 2*n.

Another way to solve dynamic programming is by Top-Down approach is by memoization

Below is the code:

C++

/* C/C++ program to count number of times S appears
   as a subsequence in T */
#include <bits/stdc++.h>
using namespace std;

int f(int i, int j, string s, string t,
      vector<vector<int> >& dp)
{
    if (t.size() - j > s.size() - i)
        return 0;

    if (j == t.size()) {
        return 1;
    }

    if (i == s.size()) {
        return 0;
    }

    if (dp[i][j] != -1) {
        return dp[i][j];
    }

    if (s[i] == t[j]) {
        return dp[i][j] = f(i + 1, j + 1, s, t, dp)
                          + f(i + 1, j, s, t, dp);
    }

    return dp[i][j] = f(i + 1, j, s, t, dp);
}

int findSubsequenceCount(string s, string t)
{
    vector<vector<int> > dp(s.size(),
                            vector<int>(t.size(), -1));
    return f(0, 0, s, t, dp);
}

// Driver code to check above method
int main()
{
    string T = "ge";
    string S = "geeksforgeeks";
    cout << findSubsequenceCount(S, T) << endl;
    return 0;
}

Java

import java.util.*;

class Program
{
    static int f(int i, int j, String s, String t,
            int dp[][])
    {
        if (t.length() - j > s.length() - i)
            return 0;

        if (j == t.length()) {
            return 1;
        }

        if (i == s.length()) {
            return 0;
        }

        if (dp[i][j] != -1) {
            return dp[i][j];
        }

        if (s.charAt(i) == t.charAt(j)) {
            return dp[i][j] = f(i + 1, j + 1, s, t, dp)
                    + f(i + 1, j, s, t, dp);
        }

        return dp[i][j] = f(i + 1, j, s, t, dp);
    }

    static int findSubsequenceCount(String s, String t)
    {
        int dp[][] = new int[s.length() + 1][t.length() + 1];
        for (int i = 0; i < s.length() + 1; i++)
            Arrays.fill(dp[i], -1);

        return f(0, 0, s, t, dp);
    }

    public static void main(String[] args)
    {
        String T = "ge";
        String S = "geeksforgeeks";
        System.out.println(findSubsequenceCount(S, T));
    }
}
// This code contributed by SRJ

Python3

# Python program to count number of times S appears
# as a subsequence in T

def f(i, j, s, t, dp):
    # if remaining characters in T are less than remaining characters in S
    if len(t) - j > len(s) - i:
        return 0

    # if we have reached the end of T
    if j == len(t):
        return 1

    # if we have reached the end of S
    if i == len(s):
        return 0

    # if we have already solved this subproblem
    if dp[i][j] != -1:
        return dp[i][j]

    if s[i] == t[j]:
        # count of S as subsequence in T where S and T are both
        # considering the current character
        count1 = f(i + 1, j + 1, s, t, dp)

        # count of S as subsequence in T where T is considering
        # the current character but S is not
        count2 = f(i + 1, j, s, t, dp)
        dp[i][j] = count1 + count2
        return dp[i][j]

    # if current characters of S and T don't match
    dp[i][j] = f(i + 1, j, s, t, dp)
    return  dp[i][j]

def findSubsequenceCount(s, t):
    # create a 2D array to store the subproblem solutions
    dp = [[-1 for j in range(len(t))] for i in range(len(s))]
    return f(0, 0, s, t, dp)

# Driver code to check above method
if __name__ == '__main__':
    T = "ge"
    S = "geeksforgeeks"
    print(findSubsequenceCount(S, T))

C#

/* C# program to count number of times S appears
   as a subsequence in T */
using System;

public class Program
{
    static int f(int i, int j, string s, string t,
            int[,] dp)
    {
        //if remaining characters in T are less than remaining characters in S
        if (t.Length - j > s.Length - i)
            return 0;

        // if we have reached the end of T
        if (j == t.Length)
        {
            return 1;
        }

        // if we have reached the end of S
        if (i == s.Length)
        {
            return 0;
        }

        // if we have already solved this subproblem
        if (dp[i, j] != -1)
        {
            return dp[i, j];
        }

        if (s[i] == t[j])
        {
            // count of S as subsequence in T where S and T are both
            // considering the current character and
            // count of S as subsequence in T where T is considering
            // the current character but S is not
            return dp[i, j] = f(i + 1, j + 1, s, t, dp)
                    + f(i + 1, j, s, t, dp);
        }

        // if current characters of S and T don't match
        return dp[i, j] = f(i + 1, j, s, t, dp);
    }

    static int findSubsequenceCount(string s, string t)
    {
        // create a 2D array to store the subproblem solutions
        int[,] dp = new int[s.Length + 1, t.Length + 1];
        for (int i = 0; i < s.Length + 1; i++)
            for (int j = 0; j < t.Length + 1; j++)
                dp[i, j] = -1;

        return f(0, 0, s, t, dp);
    }

    // Driver code to check above method
    public static void Main(string[] args)
    {
        string T = "ge";
        string S = "geeksforgeeks";
        Console.WriteLine(findSubsequenceCount(S, T));
    }
}

Javascript

// Javascript program to count number of times S appears
// as a subsequence in T
function f(i, j, s, t, dp) {
    if (t.length - j > s.length - i) {
        return 0;
    }

    if (j === t.length) {
        return 1;
    }

    if (i === s.length) {
        return 0;
    }

    if (dp[i][j] !== -1) {
        return dp[i][j];
    }

    if (s[i] === t[j]) {
        dp[i][j] = f(i + 1, j + 1, s, t, dp) + f(i + 1, j, s, t, dp);
        return dp[i][j];
    }

    return dp[i][j] = f(i + 1, j, s, t, dp);
}

function findSubsequenceCount(s, t) {
    let dp = Array(s.length).fill().map(() => Array(t.length).fill(-1));
    return f(0, 0, s, t, dp);
}

// Driver code to check above method
let T = "ge";
let S = "geeksforgeeks";
console.log(findSubsequenceCount(S, T));

Output

6

Complexity Analysis:  

• Time Complexity: O(m*n). Only one traversal of the matrix is needed, so the time Complexity is O(m*n) 
• Auxiliary Space: O(m*n) ignoring recursion stack space

If you like GeeksforGeeks and would like to contribute, you can also write an article using write.geeksforgeeks.org or mail your article to review-team@geeksforgeeks.org. See your article appearing on the GeeksforGeeks main page and help other Geeks.
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above.