Count distinct elements in every window of size k
Last Updated :
10 Jan, 2023
Given an array of size N and an integer K, return the count of distinct numbers in all windows of size K.
Examples:
Input: arr[] = {1, 2, 1, 3, 4, 2, 3}, K = 4
Output: 3 4 4 3
Explanation: First window is {1, 2, 1, 3}, count of distinct numbers is 3
Second window is {2, 1, 3, 4} count of distinct numbers is 4
Third window is {1, 3, 4, 2} count of distinct numbers is 4
Fourth window is {3, 4, 2, 3} count of distinct numbers is 3
Input: arr[] = {1, 2, 4, 4}, K = 2
Output: 2 2 1
Explanation: First window is {1, 2}, count of distinct numbers is 2
First window is {2, 4}, count of distinct numbers is 2
First window is {4, 4}, count of distinct numbers is 1
This problem has appeared in Microsoft Interview Question.
Naive Approach for finding the count of distinct numbers in all windows of size K:
Traverse the given array considering every window of size K in it and keeping a count on the distinct elements of the window
Follow the given steps to solve the problem:
- For every index, i from 0 to N – K, traverse the array from i to i + k using another loop. This is the window
- Traverse the window, from i to that index and check if the element is present or not
- If the element is not present in the prefix of the array, i.e no duplicate element is present from i to index-1, then increase the count, else ignore it
- Print the count
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
int countWindowDistinct(int win[], int K)
{
int dist_count = 0;
for (int i = 0; i < K; i++) {
int j;
for (j = 0; j < i; j++)
if (win[i] == win[j])
break;
if (j == i)
dist_count++;
}
return dist_count;
}
void countDistinct(int arr[], int N, int K)
{
for (int i = 0; i <= N - K; i++)
cout << countWindowDistinct(arr + i, K) << endl;
}
int main()
{
int arr[] = {1, 2, 1, 3, 4, 2, 3}, K = 4;
int N = sizeof(arr) / sizeof(arr[0]);
countDistinct(arr, N, K);
return 0;
}
|
Java
import java.util.Arrays;
class Test {
static int countWindowDistinct(int win[], int K)
{
int dist_count = 0;
for (int i = 0; i < K; i++) {
int j;
for (j = 0; j < i; j++)
if (win[i] == win[j])
break;
if (j == i)
dist_count++;
}
return dist_count;
}
static void countDistinct(int arr[], int N, int K)
{
for (int i = 0; i <= N - K; i++)
System.out.println(countWindowDistinct(
Arrays.copyOfRange(arr, i, arr.length), K));
}
public static void main(String args[])
{
int arr[] = {1, 2, 1, 3, 4, 2, 3}, K = 4;
countDistinct(arr, arr.length, K);
}
}
|
Python3
import math as mt
def countWindowDistinct(win, K):
dist_count = 0
for i in range(K):
j = 0
while j < i:
if (win[i] == win[j]):
break
else:
j += 1
if (j == i):
dist_count += 1
return dist_count
def countDistinct(arr, N, K):
for i in range(N - K + 1):
print(countWindowDistinct(arr[i:K + i], K))
if __name__=='__main__':
arr = [1, 2, 1, 3, 4, 2, 3]
K = 4
N = len(arr)
countDistinct(arr, N, K)
|
C#
using System;
using System.Collections.Generic;
class GFG {
static int countWindowDistinct(int[] win, int K)
{
int dist_count = 0;
for (int i = 0; i < K; i++) {
int j;
for (j = 0; j < i; j++)
if (win[i] == win[j])
break;
if (j == i)
dist_count++;
}
return dist_count;
}
static void countDistinct(int[] arr, int N, int K)
{
for (int i = 0; i <= N - K; i++) {
int[] newArr = new int[K];
Array.Copy(arr, i, newArr, 0, K);
Console.WriteLine(
countWindowDistinct(newArr, K));
}
}
public static void Main(String[] args)
{
int[] arr = {1, 2, 1, 3, 4, 2, 3};
int K = 4;
countDistinct(arr, arr.Length, K);
}
}
|
Javascript
function countWindowDistinct(win, k)
{
let dist_count = 0;
for (let i = 0; i < k; i++) {
let j;
for (j = 0; j < i; j++)
if (win[i] == win[j])
break;
if (j == i)
dist_count++;
}
return dist_count;
}
function countDistinct(arr, N, K)
{
for (let i = 0; i <= N - K; i++)
document.write(countWindowDistinct(arr.slice(i, arr.length), K) + "<br/>");
}
let arr = [1, 2, 1, 3, 4, 2, 3], K = 4;
countDistinct(arr, arr.length, K);
|
Time complexity: O(N * K2)
Auxiliary Space: O(1)
Count distinct numbers in all windows of size K using hashing:
So, there is an efficient solution using hashing, though hashing requires extra O(n) space but the time complexity will improve. The trick is to use the count of the previous window while sliding the window. To do this a hash map can be used that stores elements of the current window. The hash-map is also operated on by simultaneous addition and removal of an element while keeping track of distinct elements. The problem deals with finding the count of distinct elements in a window of length k, at any step while shifting the window and discarding all the computation done in the previous step, even though k – 1 elements are same from the previous adjacent window. For example, assume that elements from index i to i + k – 1 are stored in a Hash Map as an element-frequency pair. So, while updating the Hash Map in range i + 1 to i + k, reduce the frequency of the i-th element by 1 and increase the frequency of (i + k)-th element by 1.
Insertion and deletion from the HashMap takes constant time.
Follow the given steps to solve the problem:
- Create an empty hash map. Let the hash map be hm.
- Initialize the count of distinct elements as dist_count to 0.
- Traverse through the first window and insert elements of the first window to hm. The elements are used as key and their counts as the value in hm. Also, keep updating dist_count
- Print distinct count for the first window.
- Traverse through the remaining array (or other windows).
- Remove the first element of the previous window.
- If the removed element appeared only once, remove it from hm and decrease the distinct count, i.e. do “dist_count–“
- else (appeared multiple times in hm), then decrement its count in hm
- Add the current element (last element of the new window)
- If the added element is not present in hm, add it to hm and increase the distinct count, i.e. do “dist_count++”
- Else (the added element appeared multiple times), increment its count in hm
Below is the illustration of the above approach:
Consider the array arr[] = {1, 2, 1, 3, 4, 2, 3} and K = 4
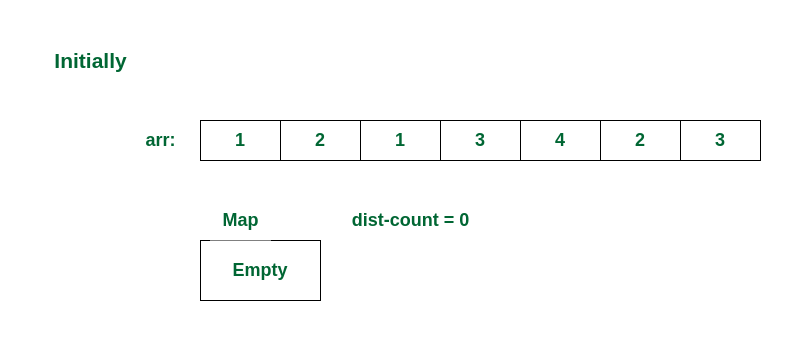
Initial State
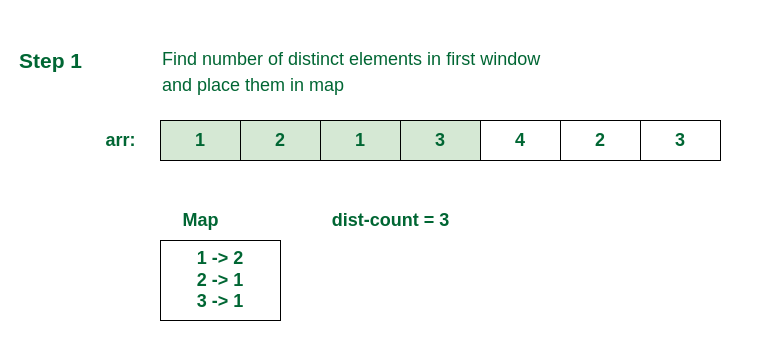
Checking in the first window
In all the remaining steps, remove the first element of the previous window and add new element of current window.
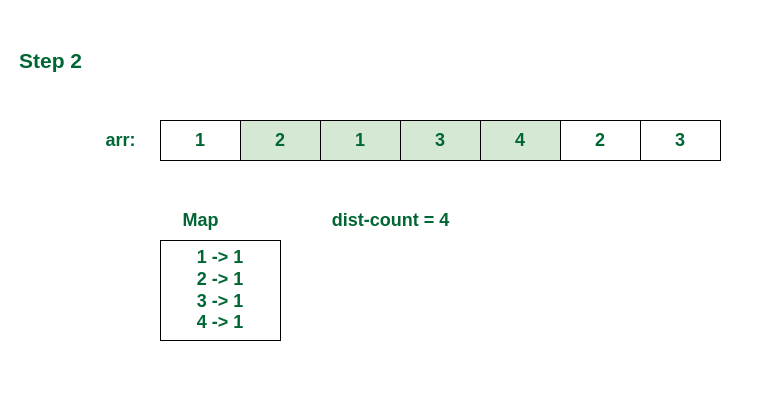
Checking in the second window
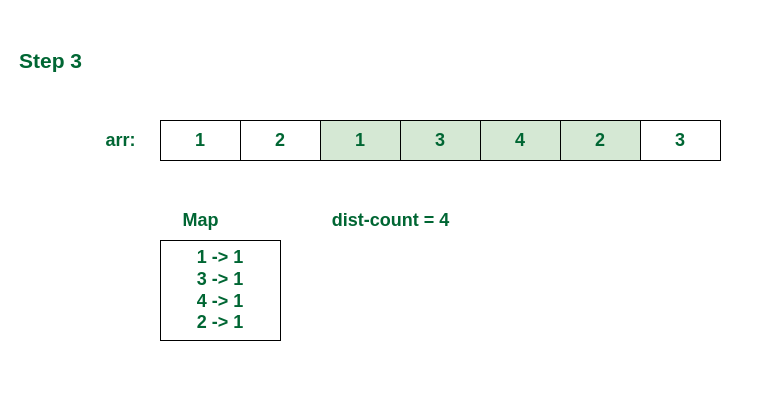
Checking in the third window
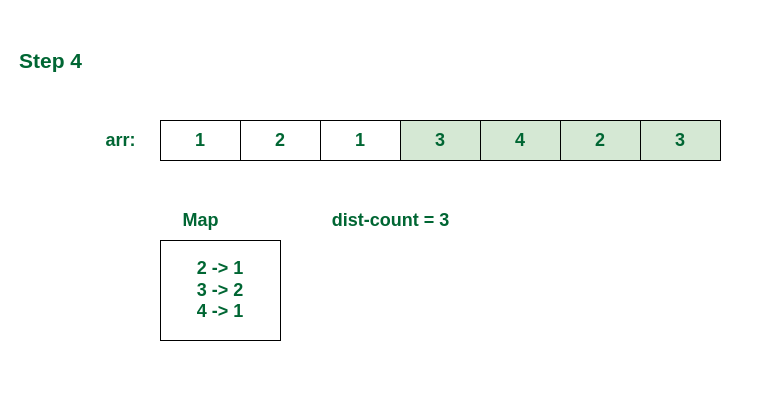
Checking the last window
Below is the implementation of the above approach:
C++
#include <iostream>
#include <unordered_map>
using namespace std;
void countDistinct(int arr[], int K, int N)
{
unordered_map<int, int> hm;
int dist_count = 0;
for (int i = 0; i < K; i++) {
if (hm[arr[i]] == 0) {
dist_count++;
}
hm[arr[i]] += 1;
}
cout << dist_count << endl;
for (int i = K; i < N; i++) {
if (hm[arr[i - K]] == 1) {
dist_count--;
}
hm[arr[i - K]] -= 1;
if (hm[arr[i]] == 0) {
dist_count++;
}
hm[arr[i]] += 1;
cout << dist_count << endl;
}
}
int main()
{
int arr[] = {1, 2, 1, 3, 4, 2, 3};
int N = sizeof(arr) / sizeof(arr[0]);
int K = 4;
countDistinct(arr, K, N);
return 0;
}
|
Java
import java.util.HashMap;
class CountDistinctWindow {
static void countDistinct(int arr[], int K)
{
HashMap<Integer, Integer> hM
= new HashMap<Integer, Integer>();
for (int i = 0; i < K; i++)
hM.put(arr[i], hM.getOrDefault(arr[i], 0) + 1);
System.out.println(hM.size());
for (int i = K; i < arr.length; i++) {
if (hM.get(arr[i - K]) == 1) {
hM.remove(arr[i - K]);
}
else
hM.put(arr[i - K], hM.get(arr[i - K]) - 1);
hM.put(arr[i], hM.getOrDefault(arr[i], 0) + 1);
System.out.println(hM.size());
}
}
public static void main(String arg[])
{
int arr[] = { 1, 2, 1, 3, 4, 2, 3 };
int K = 4;
countDistinct(arr, K);
}
}
|
Python3
from collections import defaultdict
def countDistinct(arr, K, N):
mp = defaultdict(lambda: 0)
dist_count = 0
for i in range(K):
if mp[arr[i]] == 0:
dist_count += 1
mp[arr[i]] += 1
print(dist_count)
for i in range(K, N):
if mp[arr[i - K]] == 1:
dist_count -= 1
mp[arr[i - K]] -= 1
if mp[arr[i]] == 0:
dist_count += 1
mp[arr[i]] += 1
print(dist_count)
if __name__=='__main__':
arr = [1, 2, 1, 3, 4, 2, 3]
N = len(arr)
K = 4
countDistinct(arr, K, N)
|
C#
using System;
using System.Collections.Generic;
public class CountDistinctWindow {
static void countDistinct(int[] arr, int K)
{
Dictionary<int, int> hM
= new Dictionary<int, int>();
int dist_count = 0;
for (int i = 0; i < K; i++) {
if (!hM.ContainsKey(arr[i])) {
hM.Add(arr[i], 1);
dist_count++;
}
else {
int count = hM[arr[i]];
hM.Remove(arr[i]);
hM.Add(arr[i], count + 1);
}
}
Console.WriteLine(dist_count);
for (int i = K; i < arr.Length; i++) {
if (hM[arr[i - K]] == 1) {
hM.Remove(arr[i - K]);
dist_count--;
}
else
{
int count = hM[arr[i - K]];
hM.Remove(arr[i - K]);
hM.Add(arr[i - K], count - 1);
}
if (!hM.ContainsKey(arr[i])) {
hM.Add(arr[i], 1);
dist_count++;
}
else
{
int count = hM[arr[i]];
hM.Remove(arr[i]);
hM.Add(arr[i], count + 1);
}
Console.WriteLine(dist_count);
}
}
public static void Main(String[] arg)
{
int[] arr = {1, 2, 1, 3, 4, 2, 3};
int K = 4;
countDistinct(arr, K);
}
}
|
Javascript
function countDistinct(arr, k)
{
let hM = new Map();
for (let i = 0; i < k; i++)
{
if(hM.has(arr[i]))
hM.set(arr[i], hM.get(arr[i])+1)
else
hM.set(arr[i], 1);
}
document.write(hM.size + "<br/>");
for (let i = k; i < arr.length; i++) {
if (hM.get(arr[i - k]) == 1) {
hM.delete(arr[i - k]);
}
else
hM.set(arr[i - k], hM.get(arr[i - k]) - 1);
if(hM.has(arr[i]))
hM.set(arr[i], hM.get(arr[i])+1)
else
hM.set(arr[i], 1);
document.write(hM.size + "<br/>");
}
}
let arr = [1, 2, 1, 3, 4, 2, 3];
let size = arr.length;
let k = 4;
countDistinct(arr, k, size);
|
Time complexity: O(N), A single traversal of the array is required.
Auxiliary Space: O(N), Since the hashmap requires linear space.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...