Count Arithmetic Progressions having sum S and common difference equal to D
Last Updated :
21 Mar, 2024
Given two integers S and D, the task is to count the number of Arithmetic Progressions possible with sum S and common difference D.
Examples:
Input: S = 12, D = 1
Output: 4
Explanation: Following 4 arithmetic progressions with sum 12 and common difference 1 are possible:
- {12}
- {3, 4, 5}
- {-2, -1, 0, 1, 2, 3, 4, 5}
- {-11, -10, -9, …, 10, 11, 12}
Input: S = 1, D = 1
Output: 2
Explanation: Following 2 arithmetic progressions with sum 1 and common difference 1 are possible:
- {1}
- {0, 1}
Approach: The given problem can be solved based on the following observations:

where,
S is the sum of the AP series,
a is the first term of the series,
N is the number of terms in the series,
d is a common difference
- After rearranging the above expressions:
=> 2*S = N*(2*a + (N – 1)*d) … (1)
=>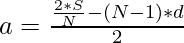 …(2)
…(2)
- From the above two expressions:
- The idea is to consider all the factors of 2*S and check if there exists any factor F such that the product of F and (2*a + (F – 1)*d) is equal to 2 * S. If found to be true, then count that factor for one of the possible AP having the given sum S.
- If there exists any factor F, such that (D * F – (2 * S / F) + D) is divisible by 2, then count that factor for one of the possible AP having the given sum S.
Follow the steps below to solve the problem:
- Initialize a variable, say answer, to store the count of APs with sum S and common difference D.
- Iterate over the range [1, ?2*S] and check if 2 * S is divisible by i, then perform the following steps:
- If the value of ((2 * S / i) + 1 – i * D) is divisible by 2, then increment answer by 1.
- If the value of (i * D – S / i + 1) is divisible by 2, then increment answer by 1.
- After completing the above steps, print the value of answer as the resultant count of APs.
Below is the implementation of the above approach:
C++
// C++ program for the above approach
#include <bits/stdc++.h>
using namespace std;
// Function to count the number of APs
// with sum S and common difference D
int countAPs(int S, int D)
{
// Multiply S by 2
S = S * 2;
// Stores the count of APs
int answer = 0;
// Iterate over the factors of 2*S
for (int i = 1; i <= sqrt(S); i++) {
// Check if i is the factor
// or not
if (S % i == 0) {
// Conditions to check if AP
// can be formed using factor F
if (((S / i) - D * i + D) % 2 == 0)
answer++;
if ((D * i - (S / i) + D) % 2 == 0)
answer++;
}
}
// Return the total count of APs
return answer;
}
// Driver Code
int main()
{
int S = 12, D = 1;
cout << countAPs(S, D);
return 0;
}
// Java program for above approach
/*package whatever //do not write package name here */
import java.io.*;
class GFG
{
// Function to count the number of APs
// with sum S and common difference D
static int countAPs(int S, int D)
{
// Multiply S by 2
S = S * 2;
// Stores the count of APs
int answer = 0;
// Iterate over the factors of 2*S
for (int i = 1; i <= Math.sqrt(S); i++) {
// Check if i is the factor
// or not
if (S % i == 0) {
// Conditions to check if AP
// can be formed using factor F
if (((S / i) - D * i + D) % 2 == 0)
answer++;
if ((D * i - (S / i) + D) % 2 == 0)
answer++;
}
}
// Return the total count of APs
return answer;
}
// Driver code
public static void main(String[] args)
{
int S = 12, D = 1;
System.out.println(countAPs(S, D));
}
}
// This code is contributed by susmitakundugoaldanga.
// C# program for the above approach
using System;
class GFG{
// Function to count the number of APs
// with sum S and common difference D
static int countAPs(int S, int D)
{
// Multiply S by 2
S = S * 2;
// Stores the count of APs
int answer = 0;
// Iterate over the factors of 2*S
for (int i = 1; i <= Math.Sqrt(S); i++) {
// Check if i is the factor
// or not
if (S % i == 0) {
// Conditions to check if AP
// can be formed using factor F
if (((S / i) - D * i + D) % 2 == 0)
answer++;
if ((D * i - (S / i) + D) % 2 == 0)
answer++;
}
}
// Return the total count of APs
return answer;
}
// Driver code
static void Main()
{
int S = 12, D = 1;
Console.Write(countAPs(S, D));
}
}
// This code is contributed by sanjoy_62.
<script>
// Javascript program for the above approach
// Function to count the number of APs
// with sum S and common difference D
function countAPs(S, D)
{
// Multiply S by 2
S = S * 2;
// Stores the count of APs
let answer = 0;
// Iterate over the factors of 2*S
for (let i = 1; i <= Math.sqrt(S); i++) {
// Check if i is the factor
// or not
if (S % i == 0) {
// Conditions to check if AP
// can be formed using factor F
if (((S / i) - D * i + D) % 2 == 0)
answer++;
if ((D * i - (S / i) + D) % 2 == 0)
answer++;
}
}
// Return the total count of APs
return answer;
}
// Driver code
let S = 12, D = 1;
document.write(countAPs(S, D));
</script>
# Python3 program for the above approach
# Function to count the number of APs
# with sum S and common difference D
def countAPs(S, D):
# Multiply S by 2
S = S * 2
# Stores the count of APs
answer = 0
# Iterate over the factors of 2*S
for i in range(1, S):
if i * i > S:
break
# Check if i is the factor
# or not
if (S % i == 0):
# Conditions to check if AP
# can be formed using factor F
if (((S // i) - D * i + D) % 2 == 0):
answer += 1
if ((D * i - (S // i) + D) % 2 == 0):
answer += 1
# Return the total count of APs
return answer
# Driver Code
if __name__ == '__main__':
S, D = 12, 1
print(countAPs(S, D));
# This code is contributed by mohit kumar 29.
Time Complexity: O(sqrt(S))
Auxiliary Space: O(1), since no extra space has been taken.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...