Count all possible N digit numbers that satisfy the given condition
Last Updated :
23 Jun, 2022
Given an integer N, the task is to count all possible N digit numbers such that A + reverse(A) = 10N – 1 where A is an N digit number and reverse(A) is reverse of A. A shouldn’t have any leading 0s.
Examples:
Input: N = 2
Output: 9
All possible 2 digit numbers are 90, 81, 72, 63, 54, 45, 36, 27 and 18.
Input: N = 4
Output: 90
Approach: First we have to conclude that if N is odd then there is no number which will satisfy the given condition, let’s prove it for N = 3,
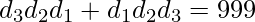 ,
,
so 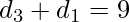 and
and 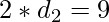 .
.
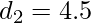 which is impossible as it is a floating point number.
which is impossible as it is a floating point number.
Now Find answer for when N is even. For example, N=4,
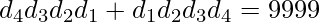
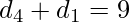 and
and 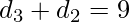 now if x + y = 9 then the number of pairs which satisfy this condition are 10.
now if x + y = 9 then the number of pairs which satisfy this condition are 10.
(0, 9), (1, 8), (2, 7), (3, 6), (4, 5), (5, 4), (6, 3), (7, 2), (8, 1), (9, 0)
Now, 1st and Nth digit cannot have the pair (0, 9) as there shouldn’t be any leading 0s in A but for all the remaining N/2-1 pairs there can be 10 pairs.
So the answer is 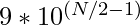 , As N is large so we will print 9 followed by N/2-1 number of 0s.
, As N is large so we will print 9 followed by N/2-1 number of 0s.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
string getCount(int N)
{
if (N % 2 == 1)
return 0;
string result = "9";
for (int i = 1; i <= N / 2 - 1; i++)
result += "0";
return result;
}
int main()
{
int N = 4;
cout << getCount(N);
return 0;
}
|
Java
class GFG
{
static String getCount(int N)
{
if (N % 2 == 1)
return "0";
String result = "9";
for (int i = 1; i <= N / 2 - 1; i++)
result += "0";
return result;
}
public static void main(String []args)
{
int N = 4;
System.out.println(getCount(N));
}
}
|
Python3
def getCount(N):
if (N % 2 == 1):
return "0"
result = "9"
for i in range (1, N // 2 ):
result = result + "0"
return result
N = 4
print(getCount(N))
|
C#
using System;
class GFG
{
static string getCount(int N)
{
if (N % 2 == 1)
return "0";
string result = "9";
for (int i = 1; i <= N / 2 - 1; i++)
result += "0";
return result;
}
public static void Main()
{
int N = 4;
Console.WriteLine(getCount(N));
}
}
|
PHP
<?php
function getCount($N)
{
if ($N % 2 == 1)
return 0;
$result = "9";
for ($i = 1; $i <= $N / 2 - 1; $i++)
$result .= "0";
return $result;
}
$N = 4;
echo getCount($N);
?>
|
Javascript
<script>
function getCount(N)
{
if (N % 2 == 1)
return "0";
let result = "9";
for (let i = 1; i <= N / 2 - 1; i++)
result += "0";
return result;
}
let N = 4;
document.write(getCount(N));
</script>
|
Time Complexity: O(N)
Auxiliary Space: O(1)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...