Convex Hull using Jarvis’ Algorithm or Wrapping
Last Updated :
07 Mar, 2024
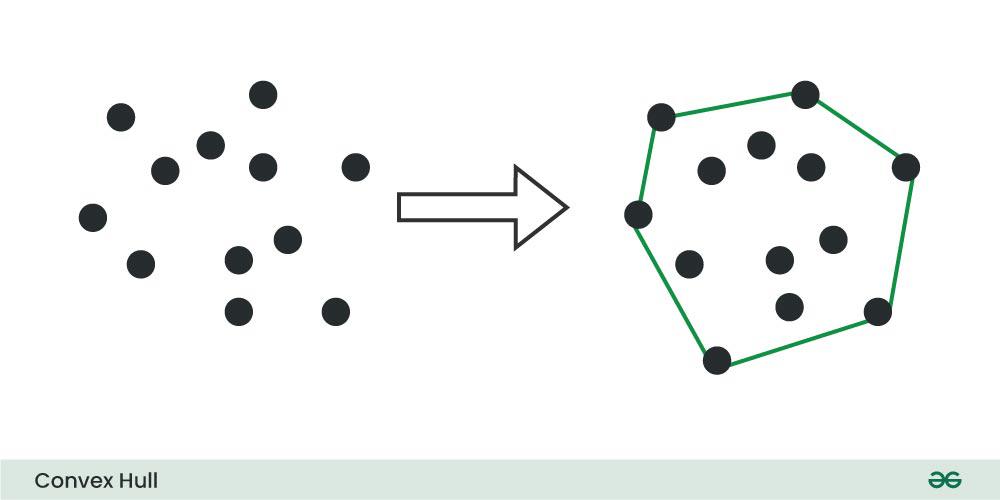
Given a set of points in the plane. the convex hull of the set is the smallest convex polygon that contains all the points of it.
We strongly recommend to see the following post first.
How to check if two given line segments intersect?
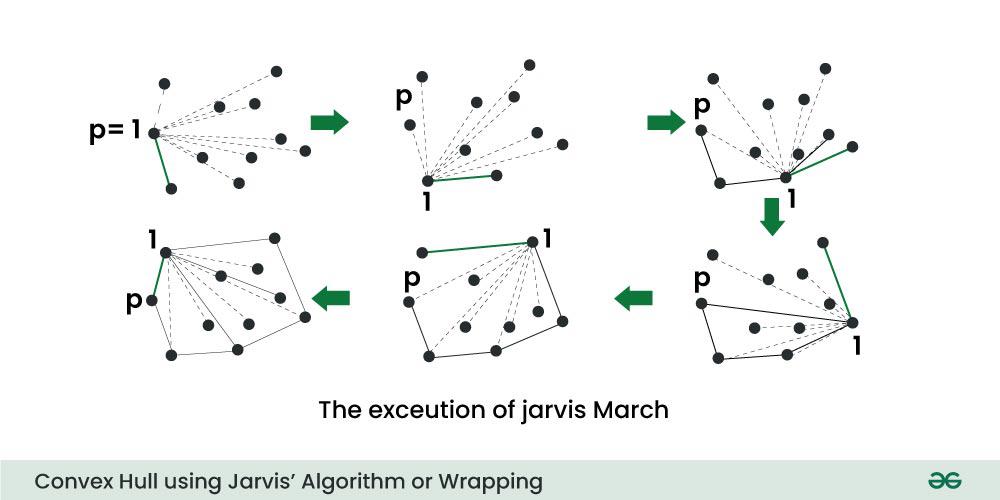
The idea of Jarvis’s Algorithm is simple, we start from the leftmost point (or point with minimum x coordinate value) and we keep wrapping points in counterclockwise direction.
The big question is, given a point p as current point, how to find the next point in output?
The idea is to use orientation() here. Next point is selected as the point that beats all other points at counterclockwise orientation, i.e., next point is q if for any other point r, we have “orientation(p, q, r) = counterclockwise”.
Algorithm:
Step 1) Initialize p as leftmost point.
Step 2) Do following while we don’t come back to the first (or leftmost) point.
2.1) The next point q is the point, such that the triplet (p, q, r) is counter clockwise for any other point r.
To find this, we simply initialize q as next point, then we traverse through all points.
For any point i, if i is more counter clockwise, i.e., orientation(p, i, q) is counter clockwise, then we update q as i.
Our final value of q is going to be the most counter clockwise point.
2.2) next[p] = q (Store q as next of p in the output convex hull).
2.3) p = q (Set p as q for next iteration).
 Below is the implementation of above algorithm.
Below is the implementation of above algorithm.
C++
#include <bits/stdc++.h>
using namespace std;
struct Point
{
int x, y;
};
int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0;
return (val > 0)? 1: 2;
}
void convexHull(Point points[], int n)
{
if (n < 3) return;
vector<Point> hull;
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
int p = l, q;
do
{
hull.push_back(points[p]);
q = (p+1)%n;
for (int i = 0; i < n; i++)
{
if (orientation(points[p], points[i], points[q]) == 2)
q = i;
}
p = q;
} while (p != l);
for (int i = 0; i < hull.size(); i++)
cout << "(" << hull[i].x << ", "
<< hull[i].y << ")\n";
}
int main()
{
Point points[] = {{0, 3}, {2, 2}, {1, 1}, {2, 1},
{3, 0}, {0, 0}, {3, 3}};
int n = sizeof(points)/sizeof(points[0]);
convexHull(points, n);
return 0;
}
|
Java
import java.util.*;
class Point
{
int x, y;
Point(int x, int y){
this.x=x;
this.y=y;
}
}
class GFG {
public static int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0;
return (val > 0)? 1: 2;
}
public static void convexHull(Point points[], int n)
{
if (n < 3) return;
Vector<Point> hull = new Vector<Point>();
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
int p = l, q;
do
{
hull.add(points[p]);
q = (p + 1) % n;
for (int i = 0; i < n; i++)
{
if (orientation(points[p], points[i], points[q])
== 2)
q = i;
}
p = q;
} while (p != l);
for (Point temp : hull)
System.out.println("(" + temp.x + ", " +
temp.y + ")");
}
public static void main(String[] args)
{
Point points[] = new Point[7];
points[0]=new Point(0, 3);
points[1]=new Point(2, 3);
points[2]=new Point(1, 1);
points[3]=new Point(2, 1);
points[4]=new Point(3, 0);
points[5]=new Point(0, 0);
points[6]=new Point(3, 3);
int n = points.length;
convexHull(points, n);
}
}
|
C#
using System;
using System.Collections.Generic;
public class Point
{
public int x, y;
public Point(int x, int y)
{
this.x = x;
this.y = y;
}
}
public class GFG
{
public static int orientation(Point p, Point q, Point r)
{
int val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0;
return (val > 0)? 1: 2;
}
public static void convexHull(Point []points, int n)
{
if (n < 3) return;
List<Point> hull = new List<Point>();
int l = 0;
for (int i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
int p = l, q;
do
{
hull.Add(points[p]);
q = (p + 1) % n;
for (int i = 0; i < n; i++)
{
if (orientation(points[p], points[i], points[q])
== 2)
q = i;
}
p = q;
} while (p != l);
foreach (Point temp in hull)
Console.WriteLine("(" + temp.x + ", " +
temp.y + ")");
}
public static void Main(String[] args)
{
Point []points = new Point[7];
points[0]=new Point(0, 3);
points[1]=new Point(2, 3);
points[2]=new Point(1, 1);
points[3]=new Point(2, 1);
points[4]=new Point(3, 0);
points[5]=new Point(0, 0);
points[6]=new Point(3, 3);
int n = points.Length;
convexHull(points, n);
}
}
|
Javascript
<script>
class Point
{
constructor(x, y)
{
this.x = x;
this.y = y;
}
}
function orientation(p, q, r)
{
let val = (q.y - p.y) * (r.x - q.x) -
(q.x - p.x) * (r.y - q.y);
if (val == 0) return 0;
return (val > 0)? 1: 2;
}
function convexHull(points, n)
{
if (n < 3) return;
let hull = [];
let l = 0;
for (let i = 1; i < n; i++)
if (points[i].x < points[l].x)
l = i;
let p = l, q;
do
{
hull.push(points[p]);
q = (p + 1) % n;
for (let i = 0; i < n; i++)
{
if (orientation(points[p], points[i], points[q])
== 2)
q = i;
}
p = q;
} while (p != l);
for (let temp of hull.values())
document.write("(" + temp.x + ", " +
temp.y + ")<br>");
}
let points = new Array(7);
points[0] = new Point(0, 3);
points[1] = new Point(2, 3);
points[2] = new Point(1, 1);
points[3] = new Point(2, 1);
points[4] = new Point(3, 0);
points[5] = new Point(0, 0);
points[6] = new Point(3, 3);
let n = points.length;
convexHull(points, n);
</script>
|
Python3
class Point:
def __init__(self, x, y):
self.x = x
self.y = y
def Left_index(points):
minn = 0
for i in range(1,len(points)):
if points[i].x < points[minn].x:
minn = i
elif points[i].x == points[minn].x:
if points[i].y > points[minn].y:
minn = i
return minn
def orientation(p, q, r):
val = (q.y - p.y) * (r.x - q.x) - \
(q.x - p.x) * (r.y - q.y)
if val == 0:
return 0
elif val > 0:
return 1
else:
return 2
def convexHull(points, n):
if n < 3:
return
l = Left_index(points)
hull = []
p = l
q = 0
while(True):
hull.append(p)
q = (p + 1) % n
for i in range(n):
if(orientation(points[p],
points[i], points[q]) == 2):
q = i
p = q
if(p == l):
break
for each in hull:
print(points[each].x, points[each].y)
points = []
points.append(Point(0, 3))
points.append(Point(2, 2))
points.append(Point(1, 1))
points.append(Point(2, 1))
points.append(Point(3, 0))
points.append(Point(0, 0))
points.append(Point(3, 3))
convexHull(points, len(points))
|
Output
(0, 3)
(0, 0)
(3, 0)
(3, 3)
Time Complexity: O(m * n), where n is number of input points and m is number of output or hull points (m <= n). For every point on the hull we examine all the other points to determine the next point.
Worst case, Time complexity: O(n2). The worst case occurs when all the points are on the hull (m = n).
Auxiliary Space: O(n), since n extra space has been taken.
Set 2- Convex Hull (Graham Scan)
Note : The above code may produce different results for different order of inputs, when there are collinear points in the convex hull. For example, it produces output as (0, 3) (0, 0) (3, 0) (3, 3) for input (0, 3), (0, 0), (0, 1), (3, 0), (3, 3) and output as (0, 3) (0, 1) (0, 0) (3, 0) (3, 3) for input as (0, 3), (0, 1), (0, 0), (3, 0), (3, 3). We generally need the farthest next point in case of collinear, we can get the desired result in case of collinear points by adding one more if condition. Please refer this modified code.
Sources:
http://www.cs.uiuc.edu/~jeffe/teaching/373/notes/x05-convexhull.pdf
http://www.dcs.gla.ac.uk/~pat/52233/slides/Hull1x1.pdf
Please write comments if you find anything incorrect, or you want to share more information about the topic discussed above
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...