Convert a tree to forest of even nodes
Last Updated :
20 Dec, 2022
Given a tree of n even nodes. The task is to find the maximum number of edges to be removed from the given tree to obtain forest of trees having even number of nodes. This problem is always solvable as given graph has even nodes.
Examples:
Input : n = 10
Edge 1: 1 3
Edge 2: 1 6
Edge 3: 1 2
Edge 4: 3 4
Edge 5: 6 8
Edge 6: 2 7
Edge 7: 2 5
Edge 8: 4 9
Edge 9: 4 10
Output : 2
By removing 2 edges we can obtain the forest with even node tree.
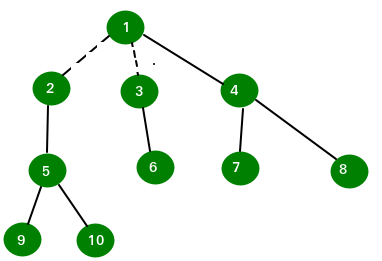
Dotted line shows removed edges. Any further removal of edge will not satisfy
the even nodes condition.
Find a subtree with even number of nodes and remove it from rest of tree by removing the edge connecting it. After removal, we are left with tree with even node only because initially we have even number of nodes in the tree and removed subtree has also even node. Repeat the same procedure until we left with the tree that cannot be further decomposed in this manner.
To do this, the idea is to use Depth First Search to traverse the tree. Implement DFS function in such a manner that it will return number of nodes in the subtree whose root is node on which DFS is performed. If the number of nodes is even then remove the edge, else ignore.
Below is implementation of this approach:
C++
#include<bits/stdc++.h>
#define N 12
using namespace std;
int dfs(vector<int> tree[N], int visit[N],
int *ans, int node)
{
int num = 0, temp = 0;
visit[node] = 1;
for (int i = 0; i < tree[node].size(); i++)
{
if (visit[tree[node][i]] == 0)
{
temp = dfs(tree, visit, ans, tree[node][i]);
(temp%2)?(num += temp):((*ans)++);
}
}
return num+1;
}
int minEdge(vector<int> tree[N], int n)
{
int visit[n+2];
int ans = 0;
memset(visit, 0, sizeof visit);
dfs(tree, visit, &ans, 1);
return ans;
}
int main()
{
int n = 10;
vector<int> tree[n+2];
tree[1].push_back(3);
tree[3].push_back(1);
tree[1].push_back(6);
tree[6].push_back(1);
tree[1].push_back(2);
tree[2].push_back(1);
tree[3].push_back(4);
tree[4].push_back(3);
tree[6].push_back(8);
tree[8].push_back(6);
tree[2].push_back(7);
tree[7].push_back(2);
tree[2].push_back(5);
tree[5].push_back(2);
tree[4].push_back(9);
tree[9].push_back(4);
tree[4].push_back(10);
tree[10].push_back(4);
cout << minEdge(tree, n) << endl;
return 0;
}
|
Java
import java.util.*;
class GFG
{
static int N = 12,ans;
static Vector<Vector<Integer>> tree=new Vector<Vector<Integer>>();
static int dfs( int visit[], int node)
{
int num = 0, temp = 0;
visit[node] = 1;
for (int i = 0; i < tree.get(node).size(); i++)
{
if (visit[tree.get(node).get(i)] == 0)
{
temp = dfs( visit, tree.get(node).get(i));
if(temp%2!=0)
num += temp;
else
ans++;
}
}
return num+1;
}
static int minEdge( int n)
{
int visit[] = new int[n+2];
ans = 0;
dfs( visit, 1);
return ans;
}
public static void main(String args[])
{
int n = 10;
for(int i = 0; i < n + 2;i++)
tree.add(new Vector<Integer>());
tree.get(1).add(3);
tree.get(3).add(1);
tree.get(1).add(6);
tree.get(6).add(1);
tree.get(1).add(2);
tree.get(2).add(1);
tree.get(3).add(4);
tree.get(4).add(3);
tree.get(6).add(8);
tree.get(8).add(6);
tree.get(2).add(7);
tree.get(7).add(2);
tree.get(2).add(5);
tree.get(5).add(2);
tree.get(4).add(9);
tree.get(9).add(4);
tree.get(4).add(10);
tree.get(10).add(4);
System.out.println( minEdge( n));
}
}
|
Python3
def dfs(tree, visit, ans, node):
num = 0
temp = 0
visit[node] = 1
for i in range(len(tree[node])):
if (visit[tree[node][i]] == 0):
temp = dfs(tree, visit, ans,
tree[node][i])
if(temp % 2):
num += temp
else:
ans[0] += 1
return num + 1
def minEdge(tree, n):
visit = [0] * (n + 2)
ans = [0]
dfs(tree, visit, ans, 1)
return ans[0]
N = 12
n = 10
tree = [[] for i in range(n + 2)]
tree[1].append(3)
tree[3].append(1)
tree[1].append(6)
tree[6].append(1)
tree[1].append(2)
tree[2].append(1)
tree[3].append(4)
tree[4].append(3)
tree[6].append(8)
tree[8].append(6)
tree[2].append(7)
tree[7].append(2)
tree[2].append(5)
tree[5].append(2)
tree[4].append(9)
tree[9].append(4)
tree[4].append(10)
tree[10].append(4)
print(minEdge(tree, n))
|
C#
using System;
using System.Collections.Generic;
class GFG
{
static int N = 12, ans;
static List<List<int>> tree = new List<List<int>>();
static int dfs(int []visit, int node)
{
int num = 0, temp = 0;
visit[node] = 1;
for (int i = 0; i < tree[node].Count; i++)
{
if (visit[tree[node][i]] == 0)
{
temp = dfs(visit, tree[node][i]);
if(temp % 2 != 0)
num += temp;
else
ans++;
}
}
return num + 1;
}
static int minEdge(int n)
{
int []visit = new int[n + 2];
ans = 0;
dfs(visit, 1);
return ans;
}
public static void Main(String []args)
{
int n = 10;
for(int i = 0; i < n + 2;i++)
tree.Add(new List<int>());
tree[1].Add(3);
tree[3].Add(1);
tree[1].Add(6);
tree[6].Add(1);
tree[1].Add(2);
tree[2].Add(1);
tree[3].Add(4);
tree[4].Add(3);
tree[6].Add(8);
tree[8].Add(6);
tree[2].Add(7);
tree[7].Add(2);
tree[2].Add(5);
tree[5].Add(2);
tree[4].Add(9);
tree[9].Add(4);
tree[4].Add(10);
tree[10].Add(4);
Console.WriteLine(minEdge(n));
}
}
|
Javascript
<script>
var N = 12, ans;
var tree = Array();
function dfs(visit, node)
{
var num = 0, temp = 0;
visit[node] = 1;
for (var i = 0; i < tree[node].length; i++)
{
if (visit[tree[node][i]] == 0)
{
temp = dfs(visit, tree[node][i]);
if(temp % 2 != 0)
num += temp;
else
ans++;
}
}
return num + 1;
}
function minEdge(n)
{
var visit = Array(n+2).fill(0);
ans = 0;
dfs(visit, 1);
return ans;
}
var n = 10;
for(var i = 0; i < n + 2;i++)
tree.push(new Array());
tree[1].push(3);
tree[3].push(1);
tree[1].push(6);
tree[6].push(1);
tree[1].push(2);
tree[2].push(1);
tree[3].push(4);
tree[4].push(3);
tree[6].push(8);
tree[8].push(6);
tree[2].push(7);
tree[7].push(2);
tree[2].push(5);
tree[5].push(2);
tree[4].push(9);
tree[9].push(4);
tree[4].push(10);
tree[10].push(4);
document.write(minEdge(n));
</script>
|
Time Complexity: O(n).
Auxiliary Space: O(n).
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...