Electric charge is a fundamental feature of matter that regulates how elementary particles are impacted by an electric or magnetic field. Positive and negative electric charge exists in discrete natural units and cannot be manufactured or destroyed. There are two sorts of electric charges: positive and negative. When two items with an overabundance of one type of charge are relatively close to each other, they repel each other. When two things with excess opposing charges, one positively charged and the other negatively charged, are in close proximity, they attract each other.
Electric charge is a property shared by many fundamental, or subatomic, particles of matter. Electrons, for example, have a negative charge while protons have a positive charge. Neutrons, on the other hand, have no charge. Experiments have discovered that the negative charge of each electron has the same magnitude as the positive charge of each proton. A charge is measured in natural units, which are equivalent to the charge of an electron or proton, which is a fundamental physical constant.
Continuous Charge Distribution
Dealt with discrete charge combinations involves q1, q2,…, qn. The mathematical treatment is easier and does not require calculus, which is one of the reasons why we limited ourselves to discrete charges. However, working with discrete charges is impracticable for many reasons, and we must instead work with continuous charge distributions. All charges are tightly bonded together with very little space between them in continuous charge distribution.
Charges can be distributed in three ways, including
- Linear charge distribution.
- Surface charge distribution.
- Volume charge distribution.
Linear Charge Distribution

Linear Charge Distribution
When charges are dispersed equally along a length, such as around the circumference of a circle or along a straight wire, this is known as linear charge distribution. The linear charge distribution is symbolized by the symbol λ.
The linear charge density λ of a wire is defined by
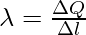
where, ∆l is on the macroscopic scale, a small line element of wire, yet it contains a significant number of microscopic charged elements and ∆Q is the charge contained in that line element.
The units for λ are C/m.
Surface Charge Distribution

Surface Charge Distribution
It is impractical to characterize the charge distribution on the surface of a charged conductor in terms of the positions of the tiny charged elements. It is more practical to consider an area element S on the conductor’s surface (which is small on a macroscopic scale but large enough to contain numerous electrons) and specify the charge Q on that element.
A surface charge density σ at the area element by
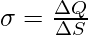
The surface charge density σ is a continuous function.
The surface charge density as stated overlooks charge quantification and charge distribution discontinuities at the microscopic level, which is a smoothed out average of the microscopic charge density across an area element ∆S, which is huge microscopically but small macroscopically, reflects macroscopic surface charge density.
The unit of surface charge density σ is C/m2.
Volume Charge Distribution

Volume Charge Distribution
Similarly, when a charge is spread uniformly over a volume then it is called volume charge distribution ρ, such as inside a sphere or a cylinder.
The volume charge density ρ (also known as charge density) is defined.
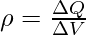
where ∆Q denotes the charge in the macroscopically small volume element ∆V, which contains a high number of microscopic charged constituents.
The unit of volume charge density ρ is C/m3.
Field due to a Continuous charge distribution
The field due to a continuous charge distribution may be calculated in the same manner as the field due to a system of discrete charges can be calculated. Assume that there is a charge density in continuous charge distribution in space. Take any suitable origin O and let r be the position vector of any point in the charge distribution. The charge density ρ may differ from point to point, i.e., it is a function of r. Divide the charge distribution into small volume elements of size ∆V. The charge in a volume element ∆V is ρ∆V.
Now, think any general point P inside or outside the distribution with position vector R. Electric field due to the charge ρ∆V is given by Coulomb’s law,
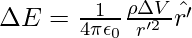
where r′ is the distance between the charge element and P, and 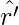 is a unit vector in the direction from the charge element to P.
is a unit vector in the direction from the charge element to P.
The total electric field owing to the charge distribution is calculated using the superposition method that is by summing over electric fields due to different volume elements.
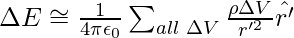
Sample Problems
Problem 1: What is linear charge distribution?
Solution:
When charges are dispersed equally along a length, such as around the circumference of a circle or along a straight wire, this is known as linear charge distribution. The linear charge distribution is symbolized by the symbol λ. The linear charge density λ of a wire is defined by
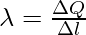
where, ∆l is on the macroscopic scale, a small line element of wire, yet it contains a significant number of microscopic charged elements and ∆Q is the charge contained in that line element. The units for λ are C/m.
Problem 2: A charge is distributed along an infinite curved line in space with linear charge distribution λ. What will be the amount of force on a point charge q kept at a certain distance from the line?
Solution:
Let the point charge is situated at a distance r from a small part dl on the line.
The charge stored in stat small part is λ.dl.
The force due to that small part will be directed towards the unit vector \hat{r}.
Therefore, force on that charge due to the entire linear charge distribution can be written as
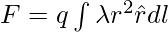
Problem 3: A circular annulus of inner radius r and outer radius R has a uniform charge density a. What will be the total charge on the annulus?
Solution:
The total surface area of the annulus is π×(R2-r2)
It has an outer radius R and an inner radius r.
The surface charge density is the amount of charge stored on the unit surface area.
The surface charge density is a.
Therefore total charge on the annulus = π×a×(R2-r2).
Problem 4: A solid nonconducting sphere of radius 1m carries a total charge of 10 C which is uniformly distributed throughout the sphere. Determine the charge density of the sphere.
Solution:
The volume of the sphere = (4/3)πr3.
where r is the radius of the sphere.
Therefore, the charge density, ρ= total charge/[(4/3)πr3].
Now substituting the values,
ρ = 10/[(4/3)πr3]
ρ= 2.38 C/m3.
But if the sphere is conducting, we have to consider the surface charge density.
Problem 5: What is surface charge distribution?
Solution:

It is impractical to characterize the charge distribution on the surface of a charged conductor in terms of the positions of the tiny charged elements. It is more practical to consider an area element S on the conductor’s surface (which is small on a macroscopic scale but large enough to contain many electrons) and specify the charge Q on that element. A surface charge density σ at the area element by
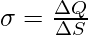
The surface charge density σ is a continuous function. The surface charge density as stated overlooks charge quantification and charge distribution discontinuities at the microscopic level. , which is a smoothed out average of the microscopic charge density across an area element ∆S, which is huge microscopically but small macroscopically, reflects macroscopic surface charge density. The unit of surface charge density σ is C/m2.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...