The continued fraction factorization method (
) is a general-purpose factorization algorithm valid for integers. It calculates factors of a given integer number without considering its unique properties. It has a sub-exponential running time. It was first described in 1931 by D. H. Lehmer and R. E. Powers and later in 1975 were developed into a computer algorithm by Michael A. Morrison and John Brillhart.
Continued Fraction:
An expression that can be expressed in the form:
(1) 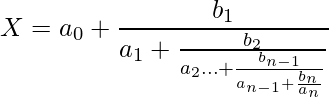
is called a Continued Fraction, where a
i and b
i are either real or complex values for all
i > = 0. When all the values of b
i‘s
are 1, then it is called a simple continued fraction.
A Simple Continued Fraction can be denoted as:
(2) ![Rendered by QuickLaTeX.com \begin{equation*} \left[a_{0} ; a_{1}, a_{2} \ldots a_{n}\right]=a_{0}+\frac{1}{a_{1}+\frac{1}{a_{2} \ldots+\frac{1}{a_{n-1}+\frac{1}{a_{n}}}}} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e617ff48613ae0a9dfb09988fbada618_l3.png)
where C
k= [a
0; a
1, a
2, …, a
n] for k<=n is the k-th convergent of the Simple Continued Fraction.
An Infinite Continued Fraction [a
0; a
1, a
2, …, a
k, …] is defined as a limit of the convergents C
k=[a0; a1, a2, …, an]
Algorithm:
This algorithm uses residues produced in the Continued Fraction of (mn)
1/2 for some m to produce a square number.
This algorithm solves the mathematical equation:
(3) 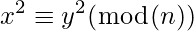
this equation is solved by calculating the value of m such that m
2 (mod(n)) has the minimum upperbound.
- CFRAC algorithm has a time complexity of:
(4) 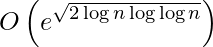
Example 1:
Input: continued_fraction((10/7))
Output: [1, 2, 3]
Explanation:
(5) ![Rendered by QuickLaTeX.com \begin{equation*} [1,2,3]=1+\frac{1}{2+\frac{1}{3}}=1+\frac{1}{\frac{7}{3}}=1+\frac{3}{7}=\frac{10}{7} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d09a338039519428e35f957e1a79a836_l3.png)
Example 2:
Input: list(continued_fraction_convergents([0, 2, 1, 2]))
Output: [0, 1/2, 1/3, 3/8]
Explanation:
(6) ![Rendered by QuickLaTeX.com \begin{equation*} \begin{array}{c} {[0,2,1,2]=0+\frac{1}{2+\frac{1}{1+\frac{1}{2}}}} \\ c_{1}=0, c_{2}=0+\frac{1}{2}=\frac{1}{2} \cdot c_{3}=0+\frac{1}{2+\frac{1}{1}}=\frac{1}{3} \cdot c_{4}=0+\frac{1}{2+\frac{1}{1+\frac{1}{2}}}=0+\frac{1}{2+\frac{1}{3}}=0+\frac{1}{2+\frac{1}{2}}=\frac{1}{\frac{1}{3}}=\frac{3}{8} \end{array} \end{equation*}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-363bcbb9bf397e493b5ff17391a00c46_l3.png)
Example 3:
Input: continued_fraction_reduce([1, 2, 3, 4, 5])
Output: 225/157
Explanation:
(7) 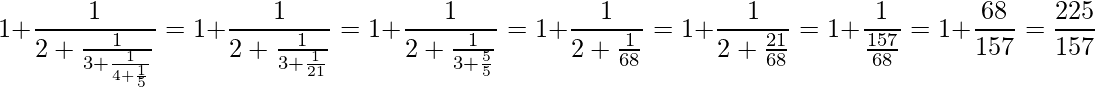
Implementation:
Code: To convert a fraction into Continued Fraction representation
from sympy.ntheory.continued_fraction import continued_fraction
from sympy import sqrt
continued_fraction(10/7)
|
Output:
[1, 2, 3]
Code 2: To convert a Continued Fraction into fraction.
from sympy.ntheory.continued_fraction import continued_fraction_reduce
continued_fraction_reduce([1, 2, 3, 4, 5])
|
Output:
225/157
Code 3: To get a list of convergents from a Continued fraction.
from sympy.core import Rational, pi
from sympy import S
from sympy.ntheory.continued_fraction import continued_fraction_convergents, continued_fraction_iterator
list(continued_fraction_convergents([0, 2, 1, 2]))
|
Output:
[0, 1/2, 1/3, 3/8]
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...