Construct a tree from Inorder and Level order traversals | Set 1

Given inorder and level-order traversals of a Binary Tree, construct the Binary Tree. Following is an example to illustrate the problem.

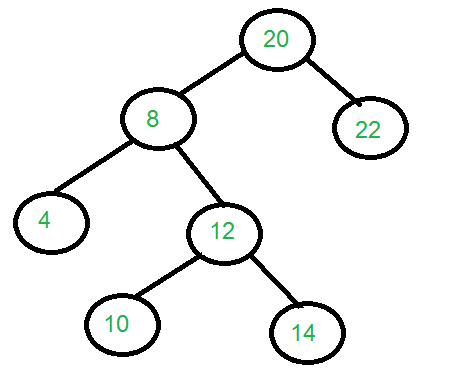
Input: Two arrays that represent Inorder
       and level order traversals of a 
       Binary Tree
in[]    = {4, 8, 10, 12, 14, 20, 22};
level[] = {20, 8, 22, 4, 12, 10, 14};

Output: Construct the tree represented 
        by the two arrays.
        For the above two arrays, the 
        constructed tree is shown in 
        the diagram on right side

The following post can be considered as a prerequisite for this. 
Construct Tree from given Inorder and Preorder traversals

Let us consider the above example.

• in[] = {4, 8, 10, 12, 14, 20, 22}; 
• level[] = {20, 8, 22, 4, 12, 10, 14};

In a Levelorder sequence, the first element is the root of the tree. So we know ’20’ is root for given sequences. By searching ’20’ in Inorder sequence, we can find out all elements on left side of ‘20’ are in left subtree and elements on right are in right subtree. So we know below structure now. 

             20
           /    \
          /      \ 
 {4,8,10,12,14}  {22}

Let us call {4,8,10,12,14} as left subarray in Inorder traversal and {22} as right subarray in Inorder traversal. 
In level order traversal, keys of left and right subtrees are not consecutive. So we extract all nodes from level order traversal which are in left subarray of Inorder traversal. To construct the left subtree of root, we recur for the extracted elements from level order traversal and left subarray of inorder traversal. In the above example, we recur for the following two arrays. 

// Recur for following arrays to construct the left subtree
In[]    = {4, 8, 10, 12, 14}
level[] = {8, 4, 12, 10, 14}

Similarly, we recur for the following two arrays and construct the right subtree.

// Recur for following arrays to construct the right subtree
In[]    = {22}
level[] = {22}

Following is the implementation of the above approach: 

C++

/* program to construct tree using inorder and levelorder
 * traversals */
#include <bits/stdc++.h>
using namespace std;

/* A binary tree node */
struct Node {
    int key;
    struct Node *left, *right;
};

/* Function to find index of value in arr[start...end] */
int search(int arr[], int strt, int end, int value)
{
    for (int i = strt; i <= end; i++)
        if (arr[i] == value)
            return i;
    return -1;
}

// n is size of level[], m is size of in[] and m < n. This
// function extracts keys from level[] which are present in
// in[].  The order of extracted keys must be maintained
int* extrackKeys(int in[], int level[], int m, int n)
{
    int *newlevel = new int[m], j = 0;
    for (int i = 0; i < n; i++)
        if (search(in, 0, m - 1, level[i]) != -1)
            newlevel[j] = level[i], j++;
    return newlevel;
}

/* function that allocates a new node with the given key  */
Node* newNode(int key)
{
    Node* node = new Node;
    node->key = key;
    node->left = node->right = NULL;
    return (node);
}

/* Recursive function to construct binary tree of size n
   from Inorder traversal in[] and Level Order traversal
   level[]. inStrt and inEnd are start and end indexes of
   array in[] Initial values of inStrt and inEnd should be 0
   and n -1. The function doesn't do any error checking for
   cases where inorder and levelorder do not form a tree */
Node* buildTree(int in[], int level[], int inStrt,
                int inEnd, int n)
{

    // If start index is more than the end index
    if (inStrt > inEnd)
        return NULL;

    /* The first node in level order traversal is root */
    Node* root = newNode(level[0]);

    /* If this node has no children then return */
    if (inStrt == inEnd)
        return root;

    /* Else find the index of this node in Inorder traversal
     */
    int inIndex = search(in, inStrt, inEnd, root->key);

    // Extract left subtree keys from level order traversal
    int* llevel = extrackKeys(in, level, inIndex, n);

    // Extract right subtree keys from level order traversal
    int* rlevel
        = extrackKeys(in + inIndex + 1, level, n - 1, n);

    /* construct left and right subtrees */
    root->left = buildTree(in, llevel, inStrt, inIndex - 1,
                           inIndex - inStrt);
    root->right = buildTree(in, rlevel, inIndex + 1, inEnd,
                            inEnd - inIndex);

    // Free memory to avoid memory leak
    delete[] llevel;
    delete[] rlevel;

    return root;
}

/* utility function to print inorder traversal of binary
 * tree */
void printInorder(Node* node)
{
    if (node == NULL)
        return;
    printInorder(node->left);
    cout << node->key << " ";
    printInorder(node->right);
}

/* Driver program to test above functions */
int main()
{
    int in[] = { 4, 8, 10, 12, 14, 20, 22 };
    int level[] = { 20, 8, 22, 4, 12, 10, 14 };
    int n = sizeof(in) / sizeof(in[0]);
    Node* root = buildTree(in, level, 0, n - 1, n);

    /* Let us test the built tree by printing Inorder
     * traversal */
    cout << "Inorder traversal of the constructed tree is "
            "\n";
    printInorder(root);

    return 0;
}

Java

// Java program to construct a tree from level order and
// and inorder traversal

// A binary tree node
class Node {
    int data;
    Node left, right;

    Node(int item)
    {
        data = item;
        left = right = null;
    }

    public void setLeft(Node left) { this.left = left; }

    public void setRight(Node right) { this.right = right; }
}

class Tree {
    Node root;

    Node buildTree(int in[], int level[])
    {
        Node startnode = null;
        return constructTree(startnode, level, in, 0,
                             in.length - 1);
    }

    Node constructTree(Node startNode, int[] levelOrder,
                       int[] inOrder, int inStart,
                       int inEnd)
    {

        // if start index is more than end index
        if (inStart > inEnd)
            return null;

        if (inStart == inEnd)
            return new Node(inOrder[inStart]);

        boolean found = false;
        int index = 0;

        // it represents the index in inOrder array of
        // element that appear first in levelOrder array.
        for (int i = 0; i < levelOrder.length - 1; i++) {
            int data = levelOrder[i];
            for (int j = inStart; j < inEnd; j++) {
                if (data == inOrder[j]) {
                    startNode = new Node(data);
                    index = j;
                    found = true;
                    break;
                }
            }
            if (found == true)
                break;
        }

        // elements present before index are part of left
        // child of startNode. elements present after index
        // are part of right child of startNode.
        startNode.setLeft(
            constructTree(startNode, levelOrder, inOrder,
                          inStart, index - 1));
        startNode.setRight(
            constructTree(startNode, levelOrder, inOrder,
                          index + 1, inEnd));

        return startNode;
    }

    /* Utility function to print inorder traversal of binary
     * tree */
    void printInorder(Node node)
    {
        if (node == null)
            return;
        printInorder(node.left);
        System.out.print(node.data + " ");
        printInorder(node.right);
    }

    // Driver program to test the above functions
    public static void main(String args[])
    {
        Tree tree = new Tree();
        int in[] = new int[] { 4, 8, 10, 12, 14, 20, 22 };
        int level[]
            = new int[] { 20, 8, 22, 4, 12, 10, 14 };
        int n = in.length;
        Node node = tree.buildTree(in, level);

        /* Let us test the built tree by printing Inorder
         * traversal */
        System.out.print(
            "Inorder traversal of the constructed tree is ");
        tree.printInorder(node);
    }
}

// This code has been contributed by Mayank Jaiswal

Python3

# Python program to construct tree using
# inorder and level order traversals

# A binary tree node


class Node:

    # Constructor to create a new node
    def __init__(self, key):
        self.data = key
        self.left = None
        self.right = None


"""Recursive function to construct binary tree of size n from
Inorder traversal ino[] and Level Order traversal level[].
The function doesn't do any error checking for cases
where inorder and levelorder do not form a tree """


def buildTree(level, ino):

    # If ino array is not empty
    if ino:

        # Check if that element exist in level order
        for i in range(0, len(level)):

            if level[i] in ino:

                # Create a new node with
                # the matched element
                node = Node(level[i])

                # Get the index of the matched element
                # in level order array
                io_index = ino.index(level[i])
                break

        # Construct left and right subtree
        node.left = buildTree(level, ino[0:io_index])
        node.right = buildTree(level, ino[io_index + 1:len(ino)])
        return node

    else:
        return None


def printInorder(node):
    if node is None:
        return

    # first recur on left child
    printInorder(node.left)

    # then print the data of node
    print(node.data, end=" ")

    # now recur on right child
    printInorder(node.right)

# Driver code


levelorder = [20, 8, 22, 4, 12, 10, 14]
inorder = [4, 8, 10, 12, 14, 20, 22]

ino_len = len(inorder)
root = buildTree(levelorder, inorder)

# Let us test the build tree by
# printing Inorder traversal
print("Inorder traversal of the constructed tree is")
printInorder(root)

# This code is contributed by 'Vaibhav Kumar'

C#

// C# program to construct a tree from
// level order and and inorder traversal
using System;

// A binary tree node
public class Node {
    public int data;
    public Node left, right;

    public Node(int item)
    {
        data = item;
        left = right = null;
    }

    public virtual Node Left
    {
        set { this.left = value; }
    }

    public virtual Node Right
    {
        set { this.right = value; }
    }
}

class GFG {
    public Node root;

    public virtual Node buildTree(int[] arr, int[] level)
    {
        Node startnode = null;
        return constructTree(startnode, level, arr, 0,
                             arr.Length - 1);
    }

    public virtual Node
    constructTree(Node startNode, int[] levelOrder,
                  int[] inOrder, int inStart, int inEnd)
    {

        // if start index is more than end index
        if (inStart > inEnd) {
            return null;
        }

        if (inStart == inEnd) {
            return new Node(inOrder[inStart]);
        }

        bool found = false;
        int index = 0;

        // it represents the index in inOrder
        // array of element that appear first
        // in levelOrder array.
        for (int i = 0; i < levelOrder.Length - 1; i++) {
            int data = levelOrder[i];
            for (int j = inStart; j < inEnd; j++) {
                if (data == inOrder[j]) {
                    startNode = new Node(data);
                    index = j;
                    found = true;
                    break;
                }
            }
            if (found == true) {
                break;
            }
        }

        // elements present before index are
        // part of left child of startNode.
        // elements present after index are
        // part of right child of startNode.
        startNode.Left
            = constructTree(startNode, levelOrder, inOrder,
                            inStart, index - 1);
        startNode.Right
            = constructTree(startNode, levelOrder, inOrder,
                            index + 1, inEnd);

        return startNode;
    }

    /* Utility function to print inorder
       traversal of binary tree */
    public virtual void printInorder(Node node)
    {
        if (node == null) {
            return;
        }
        printInorder(node.left);
        Console.Write(node.data + " ");
        printInorder(node.right);
    }

    // Driver Code
    public static void Main(string[] args)
    {
        GFG tree = new GFG();
        int[] arr = new int[] { 4, 8, 10, 12, 14, 20, 22 };
        int[] level
            = new int[] { 20, 8, 22, 4, 12, 10, 14 };
        int n = arr.Length;
        Node node = tree.buildTree(arr, level);

        /* Let us test the built tree by
        printing Inorder traversal */
        Console.Write("Inorder traversal of the "
                      + "constructed tree is "
                      + "\n");
        tree.printInorder(node);
    }
}

// This code is contributed by Shrikant13

Javascript

<script>

// inorder and level order traversals
// A binary tree node
class Node{

    // Constructor to create a new node
    constructor(key){
        this.data = key
        this.left = null
        this.right = null
    }

}

// Recursive function to construct binary tree of size n from
// Inorder traversal ino[] and Level Order traversal level[].
// The function doesn't do any error checking for cases
// where inorder and levelorder do not form a tree
function buildTree(level, ino)
{

    // If ino array is not empty
    if(ino.length > 0)
    {

        // Check if that element exist in level order
        let io_index;
        let node;
        for (let i = 0; i < level.length; i++)
        {

            if(ino.indexOf(level[i]) !== -1)
            {

                // Create a new node with
                // the matched element
                node = new Node(level[i])

                // Get the index of the matched element
                // in level order array
                io_index = ino.indexOf(level[i]);
                break

            }

        }

        // Construct left and right subtree
        node.left = buildTree(level, ino.slice(0,io_index))
        node.right = buildTree(level, ino.slice(io_index+1,ino.length))
        return node
    }

    else return null;

}

function printInorder(node){
    if(node === null)
        return

    // first recur on left child
    printInorder(node.left)

    // then print the data of node
    document.write(node.data," ")

    // now recur on right child
    printInorder(node.right)
}

// Driver code
let levelorder = [20, 8, 22, 4, 12, 10, 14];
let inorder = [4, 8, 10, 12, 14, 20, 22];

root = buildTree(levelorder, inorder);

// Let us test the build tree by
// printing Inorder traversal
document.write("Inorder traversal of the constructed tree is","</br>");
printInorder(root);

// This code is contributed by shinjanpatra

</script>

Output

Inorder traversal of the constructed tree is 
4 8 10 12 14 20 20 

An upper bound on time complexity of above method is O(n³). In the main recursive function, extractNodes() is called which takes O(n²) time.

The code can be optimized in many ways and there may be better solutions. 

Time Complexity: O(n^3)

Space Complexity: O(n) where n is the number of nodes.

Construct a tree from Inorder and Level order traversals | Set 2