Construct an Array such that cube sum of all element is a perfect square

Given the size of array N, the task is to construct an array of size N with positive integer elements such that the cube sum of all elements of this array is a perfect square.
Note: Repetitions of integers are allowed.
Example:

Input: N = 1 
Output: 4 
Explanation: Cube of 4 is 64, and 64 is perfect square.
Input: N = 6 
Output: 5 10 5 10 5 5 
Explanation: Cubic sum of array element is (5)³ + (10)³ + (5)³ + (10)³ + (5)³ + (5)³ = 2500, and 2500 is perfect square. 

Approach: The idea is to construct array of size, N which contain first N natural number. If closely observed, 

cubic sum of first N natural number: (1)³ + (2)³ + (3)³ + (4)³ + …….(N)³ is always perfect square.
as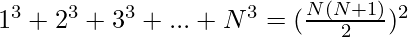 

Below is the implementation of the above approach. 

C++

// C++ program to construct an array
// that cube sum of all element
// is a perfect square

#include <bits/stdc++.h>
using namespace std;

// Function to create
// and print the array
void constructArray(int N)
{
    int arr[N];

    // initialise the array of size N
    for (int i = 1; i <= N; i++) {
        arr[i - 1] = i;
    }

    // Print the array
    for (int i = 0; i < N; i++) {
        cout << arr[i] << ", ";
    }
}

// Driver code
int main()
{
    int N = 6;

    constructArray(N);

    return 0;
}

Java

// Java program to construct array
// that cube sum of all element
// is a perfect square
import java.util.*;

class GFG{

// Function to create
// and print the array
static void constructArray(int N)
{
    int arr[] = new int[N];

    // Initialise the array of size N
    for(int i = 1; i <= N; i++)
    {
       arr[i - 1] = i;
    }

    // Print the array
    for(int i = 0; i < N; i++)
    {
        System.out.print(arr[i] + ", ");
    }
}

// Driver code
public static void main(String[] args)
{
    int N = 6;

    constructArray(N);
}
}

// This code is contributed by AbhiThakur

Python3

# Python3 program to construct
# array that cube sum of all
# element is a perfect square

# Function to create
# and print the array
def constructArray(N):

    arr = [0] * N

    # Initialise the array of size N
    for i in range(1, N + 1):
        arr[i - 1] = i;

    # Print the array
    for i in range(N):
        print(arr[i], end = ", ")

# Driver code
N = 6;
constructArray(N);

# This code is contributed by grand_master

C#

// C# program to construct array
// that cube sum of all element
// is a perfect square
using System;

class GFG{

// Function to create
// and print the array
static void constructArray(int N)
{
    int []arr = new int[N];

    // Initialise the array of size N
    for(int i = 1; i <= N; i++)
    {
       arr[i - 1] = i;
    }

    // Print the array
    for(int i = 0; i < N; i++)
    {
       Console.Write(arr[i] + ", ");
    }
}

// Driver code
public static void Main()
{
    int N = 6;

    constructArray(N);
}
}

// This code is contributed by Code_Mech

Javascript

<script>
// JavaScript program to construct an array
// that cube sum of all element
// is a perfect square

// Function to create
// and print the array
function constructArray(N)
{
    let arr = new Array(N);

    // initialise the array of size N
    for (let i = 1; i <= N; i++)
    {
        arr[i - 1] = i;
    }

    // Print the array
    for (let i = 0; i < N; i++)
    {
        document.write(arr[i] + ", ");
    }
}

// Driver code
let N = 6;
constructArray(N);

// This code is contributed by Manoj.
</script>

Output:

1, 2, 3, 4, 5, 6,

Time Complexity: O(N) where N is the size of the Array. 
Space Complexity: O(N), for creating an array to store the answer.