Construct a Turing Machine for language L = {02n1n | n>=0}
Last Updated :
14 Jun, 2020
Prerequisite –
Turing Machine
The language L = {0
2n1
n | n >= 0} represents a kind of language where we use only 2 symbols, i.e., 0 and 1. In the beginning language has some number of 0’s followed by exactly half number of 1’s . Any such string which falls in this category will be accepted by this language.
Examples :
Input : 001
Output : YES
Input : 00001
Output : NO
Input : 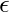 or empty string
Output : YES
or empty string
Output : YES
Basic Representation –
 Start of Computation :
Start of Computation :
The tape contains the input string w, the tape head is on the leftmost symbol of w, and the Turing machine is in the start state Q0.
Basic Idea :
The tape head reads the leftmost symbol of w, which is 0 and makes is blank then the next left most 0 is made blank after this we traverse to the rightmost 1 of the string and make it blank. In nth is way we have reduced the string to 0
2n-21
n-1.If the string belongs to language L then at end empty string will be left and hence gets accepted by the machine.
 Meanings of symbols used:
Meanings of symbols used:
R, L – direction of movement of one unit on either side.
B-Blank.
0, 1 – symbols whose combination string is to be tested.
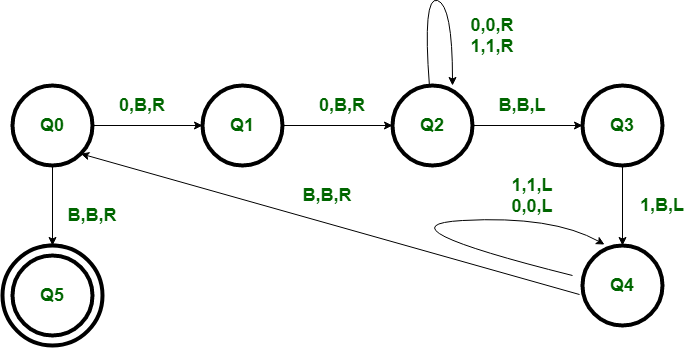
Working Procedure :
- Step-1:
As we know the string will have twice number of zeros in the starting than the number of ones. So, we will first make the first two zeros Blank and go from state Q0 to Q1 and from state Q1 to Q2.
- Step-2:
After making them Blank we will traverse to the end of the string till we get the rightmost 1 in state Q3 and make it Blank reaching state Q4.
- Step-3:
Now we will traverse back till we get the left most zero in the string and return to the state Q0 from Q4.
- Step-4:
We are just reducing the string by making left most two zeros Blank and rightmost 1 Blank and if the string belongs to the language then it will be left empty and hence get accepted at state Q5 which is Final state. If the string is empty it will also get accepted at Q5.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...