Assume a fast truck collides with a stopped automobile, causing the automobile to begin moving. What exactly is going on behind the scenes? In this case, as the truck’s velocity drops, the automobile’s velocity increases, and therefore the momentum lost by the truck is acquired by the automobile. What do you think? Let’s learn more about the momentum and its discussion below:
What is Momentum?
Momentum or Linear momentum is defined as the product of the mass of an object and its velocity. Or in other words momentum is termed as “mass in motion.” Because all objects have mass, if an object is moving, it has momentum, its mass is in motion.
Any change in the mass or the velocity of the system causes a change in linear momentum. Mass of an object and velocity is directly proportional to linear momentum. Linear momentum can be expressed as:
Momentum = mass × velocity
or
p = m × v
where p is the linear momentum, m is the mass and v is the velocity of the object.
From this, it can be concluded that the more the mass of the object or velocity more will be the linear momentum.
Momentum is a vector quantity because it has both direction and magnitude. Its direction is the same as that of velocity.
The kilogram-meter-per-second is the SI unit of momentum (kg m/s).
Graphically, the relationship between mass and velocity in terms of momentum can be plotted as:
Because the application of an unbalanced force causes a change in the velocity of the object, it follows that a force also causes a change in momentum. The momentum at the start of the time interval is defined as the initial momentum, and the momentum at the end of the time interval is defined as the final momentum.
Laws of Motion
The three laws of motion provided by Newton are stated below:
- First Law of Motion: This law is also called as Law of inertia and is stated as: A body continues to be in the state of rest or in the state of motion unless it is compelled by some external force.
- Second Law of Motion: According to Newton’s Second Law of Motion, the rate of change of momentum of a body is directly proportional to the external force applied on it and the change takes place in the direction of force applied.
- Third Law of Motion: According to Newton’s Third Law of Motion, For every action, there is an equal and opposite reaction, and they act on two different bodies. Action and reaction forces are equal and opposite, and they act on two different bodies.
The law of conservation of linear momentum is a significant result of Newton’s third law of motion in accordance with the second law of motion.
Law of Conservation of Momentum
The conservation of momentum principle states that if two objects collide, the total momentum before and after the collision will be the same if no external force acts on the colliding objects. Or simply it can be stated as:
If there is no external force acting on the system, the momentum is constant. When two objects collide in an isolated system, the total momentum of the two objects before the collision equals the total momentum of the two objects after the collision.
When the net external force is zero, the momentum of the system remains constant, as expressed mathematically by the conservation of the linear momentum formula.
Final momentum (Pf) = Initial momentum (Pi)
From this it can be interpreted as, for any two or more bodies in an isolated system acting upon each other, their total momentum remains constant unless an external force is applied. Thus, it can be said that momentum can neither be created nor destroyed. This law is valid only for linear motion. Internal forces cannot change the total momentum of the system however they may change the momentum of each particle of the system.
For instance, in a rocket, fuel is burnt due to which gases are ejected downwards. Then the rocket moves up to conserve momentum. Fuel in a jet plane burns and ejects gases in a backward direction. Therefore, by conservation of momentum, the plane moves ahead.
Derivation of Conservation of Momentum
Let us consider two bodies A and B with initial velocities u1 and u2 respectively. After some time, they undergo collision. After the collision, the velocities of A and B will become v1 and v2. Let the time of contact between two bodies is t and m1 and m2 be the masses of bodies A and B respectively.
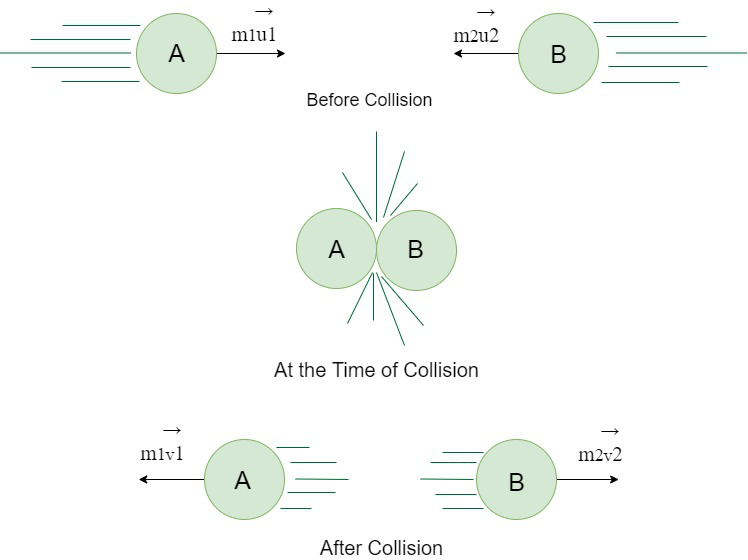
Pictorial representation for Conservation of Momentum
Let’s calculate the change in momentum for body A and it is represented by pA and is given by,
pA = m1 (v1 – u1)
Let’s calculate the change in momentum for body B and it is represented by pB and is given by,
pB = m2 (v2 – u2)
Now, from Newton’s Third Law of Motion it can be written as,
FAB = -FBA ……(1)
where FAB is the force acting on A due to B and FBA is the force acting on B due to A.
Now, from Newton’s Second Law of Motion it can be written as,
FAB = m1 a1 and ……(2)
FBA = m2 a2 ……(3)
where a1 and a2 are the acceleration of bodies A and B.
Therefore, substitute equation (2) and (3) in equation (1) as,
m1 a1 = m2 a2
Therefore, this implies that,
m1 (v1 – u1) / t = m2 (v2 – u2) / t
m1 (v1 – u1) = m2 (v2 – u2)
m1 u1 + m2 u2 = m1 v1 + m2 v2 ……(4)
this equation (4) represents the equation of law of conservation of momentum.
where L.H.S represents the total momentum of bodies A and B before the collision and R.H.S represents the total momentum of bodies A and B after the collision.
Thus, from this it is concluded that momentum is conserved.
Sample Problems
Problem 1: A body of mass 10 kg is accelerated uniformly from a velocity of 5 m/sec to 10 m/sec in 5 sec. Calculate the initial and final momentum of the body. Also, find the magnitude of the force acting on that body?
Solution:
Given
Mass of the body, m = 10 kg.
Initial velocity of the body, u = 5 m/s.
Final velocity of the body, v = 10 m/s.
Time taken by that body, t = 5 s.
Therefore,
Initial momentum of the body, pi = m × u
= 10 kg × 5 m/s
= 50 kg m s-1
Final momentum of the body, pf = m×v
= 10 kg × 10 m s-1
= 100 kg m s-1
Force acting on that body, F = m × (v-u) / t
= 10 × (10 – 5) / 5
= 10 N
Initial momentum and Final momentum and force acting on that body are 50 kg m s-1 and 100 kg m s-1 and 10 N respectively.
Problem 2: A force produces an acceleration of 16 m/s2 in a mass of 0.5 kg and an acceleration of 4.0 m/s2 in an unknown mass when applied separately. If both masses are tied together, what will be the acceleration under the same force?
Solution:
Given that,
Mass of first object = 0.5 kg
Acceleration acting on first object = 16 m/s2
Let mass of the second object be m.
Acceleration acting on second object = 4 m/s2
Let us calculate the force acting on the first object and let it be F
We know that
Force, F = m × a ……(1)
where m and a be the mass and acceleration of the body.
F = 0.5×16
= 8 N
Since both objects are tied together, Force acting on both objects are same.
Let us calculate the mass of the second body from (1)
m= F/a
8/4 = 2 kg
Thus, Mass of second body = 2 kg
Let a1 be the acceleration acting on both objects when both objects are tied and Force F is acting on them
a1 = F / (m + m1)
= 8/(0.5+2)
= 8/2.5
= 3.2 m/s2
Thus, the acceleration under the same force will be 3.2 m/s2.
Problem 3: A car is an acceleration at 20 m/s2 and after some time it accelerates at 40 m/s2 what is the ratio of force exerted by the engines?
Solution:
Given that,
The initial acceleration, a1 = 20 m/s2
The final acceleration, a2 = 40 m/s2
Therefore, the initial and the final force is,
F1 = m × a1
F2 = m × a2
And their ratios is,
F1/F2 = m × a1 / m × a2
F1/F2 = a1/a2
F1/F2 = 20/40
F1:F2 = 1:2
Problem 4: What will be the acceleration when 20N of force is applied on a 100 kg block?
Solution:
Given that,
The force, F = 20 N.
The mass of the block, m =100 kg.
Since, force is defined as,
F = m x a
20 N = 100 kg x a
a = 20 N /100 kg
a = 0.2 m/s2
Problem 5: If a constant force of 5 N is constantly applied on a block of 5 kg, How much the acceleration of the block?
Solution:
Given that,
The force, F = 5 N.
The Mass, m = 5 kg.
The initial velocity, u = 0 m/s2 .
The final velocity, v = 20 m/s2
Since,
F = ma
or
a = F / m
Therefore,
a = 5 N / 5 kg
= 1 m/s2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...