Concatenate the strings in an order which maximises the occurrence of subsequence “ab”
Last Updated :
28 Mar, 2022
Given N strings containing of characters ‘a’ and ‘b’. These string can be concatenated in any order to make a single final string S. The score of the final string S is defined as the number of occurrences of the subsequence “ab” in it. Now, the task is to concatenate the string in such a way that the score of the final string is maximized. Print the score of the final string.
Examples:
Input: arr[] = {“bab”, “aa”, “ba”, “b”}
Output: 13
If we combine the strings in the order arr[1] + arr[2] + arr[0] + arr[3]
then the final string will be “aabababb” which has a maximum score of 13.
Input: arr[] = {“aaba”, “ab”, “ba”}
Output: 10
Approach: Let us take any two strings S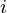 and S
and S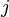 where 1 <= i, j <= N
where 1 <= i, j <= N
Let number of occurrences of ‘a’ and ‘b’ in S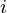 be count
be count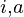 and count
and count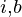 respectively.
respectively.
Similarly, let number of occurrences of ‘a’ and ‘b’ in S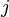 be count
be count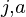 and count
and count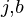 respectively.
respectively.
Also, let count of subsequences ‘ab’ within S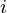 and S
and S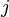 be score
be score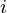 and score
and score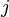 respectively.
respectively.
We will calculate number of subsequences ‘ab’ in S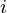 + S
+ S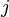 assuming that S
assuming that S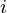 occurs before S
occurs before S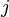 in the combined string:
in the combined string:
ans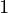 = score
= score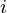 + score
+ score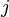 + count
+ count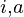 *count
*count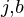
as each ‘a’ in S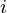 will combine with each ‘b’ in S
will combine with each ‘b’ in S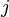 to create subsequence ‘ab’.
to create subsequence ‘ab’.
If we assume S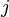 to occur before S
to occur before S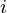 , similarly:
, similarly:
ans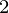 = score
= score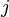 + score
+ score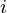 + count
+ count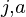 *count
*count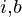
So, if ans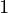 > ans
> ans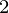 then we have to place S
then we have to place S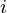 before S
before S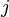 , else we will place S
, else we will place S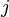 before S
before S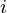 .
.
Note that the value of score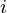 and score
and score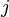 does not matter while sorting as they contribute to ans
does not matter while sorting as they contribute to ans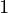 and ans
and ans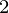 equally.
equally.
It is therefore sufficient to check if count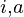 *count
*count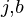 > count
> count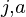 *count
*count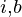 .
.
We can do this using a custom sort function as implemented in the code below.
Finally, we need to count such subsequences ‘ab’ in the combined string. For every occurrence of ‘b’, it can be combined with any ‘a’ that occurred before it to make the subsequence ‘ab’.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
bool customSort(string s1, string s2)
{
int count_a1 = 0, count_b1 = 0;
for (int i = 0; i < s1.size(); i++) {
if (s1[i] == 'a')
count_a1++;
else
count_b1++;
}
int count_a2 = 0, count_b2 = 0;
for (int i = 0; i < s2.size(); i++) {
if (s2[i] == 'a')
count_a2++;
else
count_b2++;
}
if (count_a1 * count_b2 > count_b1 * count_a2) {
return 1;
}
else {
return 0;
}
}
string concatenateStrings(string S[], int N)
{
string str = "";
for (int i = 0; i < N; i++)
str += S[i];
return str;
}
int getMaxScore(string S[], int N)
{
sort(S, S + N, customSort);
string combined_string = concatenateStrings(S, N);
int final_score = 0, count_a = 0;
for (int i = 0; i < combined_string.size(); i++) {
if (combined_string[i] == 'a') {
count_a++;
}
else {
final_score += count_a;
}
}
return final_score;
}
int main()
{
string S[] = { "bab", "aa", "ba", "b" };
int N = sizeof(S) / sizeof(string);
cout << getMaxScore(S, N);
return 0;
}
|
Java
import java.util.*;
class Gfg
{
public static boolean customSort(String s1, String s2)
{
int count_a1 = 0, count_b1 = 0;
for(int i = 0; i < s1.length(); i++)
{
if(s1.charAt(i) == 'a')
{
count_a1++;
}
else
{
count_b1++;
}
}
int count_a2 = 0, count_b2 = 0;
for(int i = 0; i < s2.length(); i++)
{
if(s2.charAt(i) == 'a')
{
count_a2++;
}
else
{
count_b2++;
}
}
if(count_a1 * count_b2 > count_b1 * count_a2)
{
return true;
}
else
{
return false;
}
}
public static String concatenateStrings(String S[],int N)
{
String str="";
for(int i = 0; i < N; i++)
{
str += S[i];
}
return str;
}
public static int getMaxScore(String S[],int N)
{
Arrays.sort(S);
String combined_string = concatenateStrings(S, N);
int final_score = 0, count_a = 0;
for (int i = 0; i < combined_string.length(); i++) {
if (combined_string.charAt(i) == 'a') {
count_a++;
}
else {
final_score += count_a;
}
}
return final_score;
}
public static void main(String []args)
{
String S[] = { "aa", "bb", "aab", "bab"};
int N = S.length;
System.out.println(getMaxScore(S, N) - 10);
}
}
|
Python 3
def customSort(s1, s2):
count_a1 = 0
count_b1 = 0
for i in range(len(s1)):
if (s1[i] == 'a'):
count_a1 += 1
else:
count_b1 += 1
count_a2 = 0
count_b2 = 0
for i in range(len(s2)):
if(s2[i] == 'a'):
count_a2 += 1
else:
count_b2 += 1
if (count_a1 * count_b2 > count_b1 * count_a2):
return 1
else:
return 0
def concatenateStrings(S, N):
str = ""
for i in range(N):
str += S[i]
return str
def getMaxScore(S, N):
S.sort()
combined_string = concatenateStrings(S, N)
final_score = 0
count_a = 0
for i in range(len(combined_string)):
if (combined_string[i] == 'a'):
count_a += 1
else:
final_score += count_a
return final_score
if __name__ == '__main__':
S = ["aa", "bb", "aab", "bab"]
N = len(S)
print(getMaxScore(S, N)-10)
|
C#
using System;
class GFG
{
static bool customSort(string s1, string s2)
{
int count_a1 = 0, count_b1 = 0;
for(int i = 0; i < s1.Length; i++)
{
if(s1[i] == 'a')
{
count_a1++;
}
else
{
count_b1++;
}
}
int count_a2 = 0, count_b2 = 0;
for(int i = 0; i < s1.Length; i++)
{
if(s2[i] == 'a')
{
count_a2++;
}
else
{
count_b2++;
}
}
if(count_a1 * count_b2 > count_b1 * count_a2)
{
return true;
}
else
{
return false;
}
}
static string concatenateStrings(string[] S, int N)
{
string str = "";
for(int i = 0; i < N; i++)
{
str += S[i];
}
return str;
}
static int getMaxScore(string[] S, int N)
{
Array.Sort(S);
string combined_string = concatenateStrings(S, N);
int final_score = 0, count_a = 0;
for(int i = 0; i < combined_string.Length; i++)
{
if(combined_string[i] == 'a')
{
count_a++;
}
else
{
final_score += count_a;
}
}
return final_score;
}
static public void Main ()
{
string[] S = {"aa", "bb", "aab", "bab"};
int N = S.Length;
Console.WriteLine(getMaxScore(S, N) - 10);
}
}
|
Javascript
<script>
function customSort(s1,s2)
{
let count_a1 = 0, count_b1 = 0;
for(let i = 0; i < s1.length; i++)
{
if(s1[i] == 'a')
{
count_a1++;
}
else
{
count_b1++;
}
}
let count_a2 = 0, count_b2 = 0;
for(let i = 0; i < s2.length; i++)
{
if(s2[i] == 'a')
{
count_a2++;
}
else
{
count_b2++;
}
}
if(count_a1 * count_b2 > count_b1 * count_a2)
{
return true;
}
else
{
return false;
}
}
function concatenateStrings(S,N)
{
let str="";
for(let i = 0; i < N; i++)
{
str += S[i];
}
return str;
}
function getMaxScore(S,N)
{
S.sort();
let combined_string = concatenateStrings(S, N);
let final_score = 0, count_a = 0;
for (let i = 0; i < combined_string.length; i++) {
if (combined_string[i] == 'a') {
count_a++;
}
else {
final_score += count_a;
}
}
return final_score;
}
let S=[ "aa", "bb", "aab", "bab"];
let N = S.length;
document.write(getMaxScore(S, N) - 10);
</script>
|
Time Complexity: O(N * log N)
Auxiliary Space: O(N)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...