Integrals are a very important part of the calculus. They allow us to calculate the anti-derivatives, that is given a function’s derivative, integrals give the function as output. Other important applications of integrals include calculating the area under the curve, the volume enclosed by a surface, etc. While the previous application mostly involves indefinite integrals, the latter one requires the boundaries to be well-defined and the integral is calculated in between those boundaries only. Such integrals are called definite integrals.
Definite Integrals
Definite integrals are mostly used to calculate the areas and the volumes enclosed by the curves. Usually, the area is calculated using well-defined formulas for rectangles, circles, and squares, etc. In real life the shapes are not that simple, thus for calculating the areas for any arbitrary shape we use the definite integrals. For a function f(x) defined on the interval [a, b], the definite integral between these limits is given by,
Here a is called the lower limit of the function and b is called the higher limit of the function.
Given a function f(x) that is continuous on the interval [a, b] we divide the interval into n subintervals of equal width,  and from each interval choose a point
and from each interval choose a point  . Then the definite integral of f(x) from a to b is,
. Then the definite integral of f(x) from a to b is,

The above figure explains the limit definition, as we increase the number of rectangles under the curve the approximated area becomes closer and closer to the actual area under the figure.
Fundamental Theorem of Calculus
The area of the region bounded by the curve f(x) between the ordinates x = a and x = b and the x-axis is given by 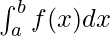 . Let’s say x is any point between the limits, then
. Let’s say x is any point between the limits, then 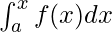 represents the area of the region from a to x. In other words, the area of this shaded region from “a” up until the value x is called the area function. It is given by,
represents the area of the region from a to x. In other words, the area of this shaded region from “a” up until the value x is called the area function. It is given by,
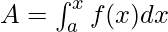

Based on this definition, two fundamental theorems of calculus are defined.
First Fundamental Theorem of Calculus
Let f(x) be a continuous function on the closed interval [a, b] and let A(x) be the area function.
Then, A'(x) = f(x), for all x ∈ [a, b].
Second Fundamental Theorem of Calculus
Let f(x) be a continuous function on the closed interval [a, b] and let F(x) be the anti-derivatives of the function f(x). Then,
![Rendered by QuickLaTeX.com \int^{b}_{a}f(x)dx = [F(x)]^{b}_{a} = F(b) - F(a)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7655c28275398f1c27e64d9f27164a3f_l3.png)
Area under the Curve
The area under the curve is given by the definite integrals. We know that the area is always a positive quantity, but while using the definite integrals, sometimes the area that comes out is negative. For example, consider the two functions below, one lies completely above the x-axis, the other one has some part that lies below the x-axis. In such cases, the two areas might cancel out each other.

In this case, the area is given by,
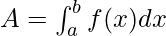

For this case, the negative and positive areas must be calculated separately and only the magnitude of their areas must be added.
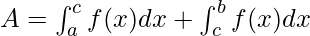
Definite Integrals of Rational Function
For calculating the definite integrals for such functions, these functions are broken down using algebraic manipulation.
Question: Calculate the value of the following integral
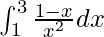
Solution:
![Rendered by QuickLaTeX.com \int^{3}_{1}\frac{1 - x}{x^2}dx \\ = \int^{3}_{1}( \frac{1}{x^2} - \frac{1}{x})dx \\ = \int^{3}_{1}( \frac{1}{x^2} )dx- \int^{3}_{1}(\frac{1}{x})dx \\ = [\frac{-1}{x}]^3_1 - [log(x)]^{3}_{1} \\ = 1 - \frac{1}{3} - (log(3) - log(1)) \\ = \frac{2}{3} - log(3)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7bf403797a8aeb73512f84c5b3597e5e_l3.png)
Definite Integrals of Radical Functions
For calculating the definite integrals for such functions, we use the reverse power rule.
Question: Calculate the value of the following integral
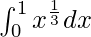
Solution:
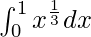
Using the reversed power rule,
![Rendered by QuickLaTeX.com \int^{1}_{0}x^{\frac{1}{3}}dx \\ = [\frac{x^{\frac{4}{3}}}{\frac{3}{4}}]^{1}_{0} \\ = \frac{4}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3ec6d1a7b02650f9026c247e0f465fdc_l3.png)
Definite Integrals of Trigonometric Functions
For calculating the definite integrals for such functions, we use the reverse power rule.
Question: Calculate the value of the following integral
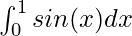
Solution:
![Rendered by QuickLaTeX.com \int^{1}_{0}sin(x)dx \\ = [-cos(x)]^{1}_{0} \\ = 1 - cos(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a87c113a8904c511ddbc28c23d7db87c_l3.png)
Definite Integrals of Natural Logarithmic Function
For calculating the definite integrals for such functions, we use the following identity.
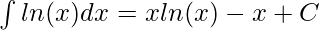
Question: Calculate the value of the following integral
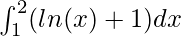
Solution:
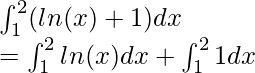
Using the formula mentioned above,
![Rendered by QuickLaTeX.com \int^{2}_{1} ln(x)dx + \int^{2}_{1} 1dx \\ = [xln(x) - x]^2_1 + [x]^2_1 \\ = ((2ln(2) - 2) - (1ln(1) - 1)) + (2 - 1) \\ = (2ln(2) - 1) + 1\\ = 2ln(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ccf022742440997214a3cf473bfd0481_l3.png)
Let’s look at some sample problems
Sample Problems
Question 1: Calculate the value of the following integral
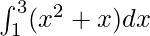
Solution:
![Rendered by QuickLaTeX.com \int^{3}_{1}(x^2 + x)dx \\ = \int^{3}_{1}x^2dx + \int^{3}_{1}xdx \\ = [\frac{x^3}{3}]^3_1 + [\frac{x^2}{2}]^3_1 \\ = 9 - \frac{1}{3} + \frac{9}{2} - \frac{1}{2} \\ = 12 - \frac{1}{3} \\ = \frac{35}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-888a1508fc832bd1e5613aed4cf78ef6_l3.png)
Question 2: Calculate the value of the following integral
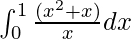
Solution:
![Rendered by QuickLaTeX.com \int^{1}_{0}\frac{(x^2 + x)}{x}dx \\ = \int^{1}_{0}xdx + \int^{1}_{0}1dx \\ = [\frac{x^2}{2}]^1_0 + [x]^{1}_{0} \\ = \frac{1}{2} + 1 \\ = \frac{3}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a080002380bdf0b84c42d296f7aabf46_l3.png)
Question 3: Calculate the value of the following integral
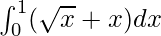
Solution:
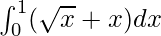
Using the reversed power rule
![Rendered by QuickLaTeX.com \int^{1}_{0}(\sqrt{x} + x)dx \\ =[\frac{x^{\frac{3}{2}}}{\frac{3}{2}} + x^2]^1_0 \\ = [\frac{2x^{\frac{3}{2}}}{3} + x^2]^1_0 \\ = \frac{2}{3} + 1 \\ = \frac{5}{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-84170d5875b60a5e8507cc2980ec48f0_l3.png)
Question 4: Calculate the value of the following integral
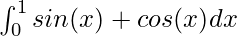
Solution:
![Rendered by QuickLaTeX.com \int^{1}_{0}sin(x) + cos(x)dx \\ = [-cos(x) + sin(x)]^1_0 \\ = [-cos(1) + sin(1)] - [1] \\ = sin(1) - cos(1) - 1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9508a6fe38212afa4c9a7a642dbf4b4a_l3.png)
Question 5: Calculate the value of the following integral
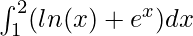
Solution:
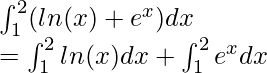
Using the formula mentioned above,
![Rendered by QuickLaTeX.com \int^{2}_{1} ln(x)dx + \int^{2}_{1} e^xdx \\ = [xln(x) - x]^2_1 + [e^x]^2_1 \\ = ((2ln(2) - 2) - (1ln(1) - 1)) + (e^2 - e) \\ = (2ln(2) - 1) + e^2 - e\\ = 2ln(2) + e^2 -e -1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cd5a6024037c844dad62add2aa92be9b_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...