Computer Graphics – Reflection Transformation in 3D
Last Updated :
22 Jun, 2022
Reflection in 3D space is quite similar to the reflection in 2D space, but a single difference is there in 3D, here we have to deal with three axes (x, y, z). Reflection is nothing but a mirror image of an object.
Three kinds of Reflections are possible in 3D space:
- Reflection along the X-Y plane.
- Reflection along Y-Z plane.
- Reflection along X-Z plane.
1. Reflection along the X-Y plane: This is shown in the following figure –
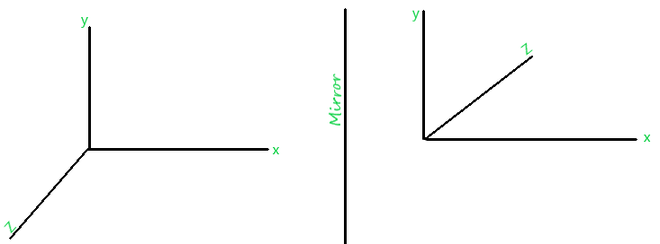
Reflection along x-y plane
The Reflection transformation matrix is used to perform the reflection operation over the 3D image, which is as follows:
![Rendered by QuickLaTeX.com \hspace{4.5cm} \Large R_{xy} =\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-81246286fa513459baa020f8f91b203f_l3.png)
Consider, a point P[x, y, z] which is in 3D space is made to reflect along X-Y direction after reflection P[x, y, z] becomes P'[x’ ,y’ ,z’].
![Rendered by QuickLaTeX.com \hspace{4.5cm} \Large P'[x\,\,y\,\,z\,\,1]=P[x\,\,y\,\,z\,\,1].R_{xy}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b0bc52c05a02d0a0ef045836a82d5d4d_l3.png)
2. Reflection along the Y-Z plane: This is shown in the following figure –
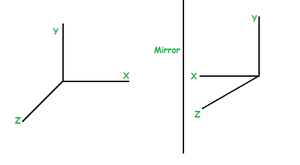
Reflection along the Y-Z plane
The reflection transformation matrix for y-z axes is as follows:
![Rendered by QuickLaTeX.com \hspace{4.5cm} \Large R_{yz} =\left[\begin{matrix}-1&0&0&0\\ 0&1&0&0\\ 0&0&1&0\\0&0&0&1\end{matrix}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0e0999bac8303011539550a8ccccd708_l3.png)
Consider, a point P[x, y, z] which is in 3D space is made to reflect along Y-Z direction, after reflection P[x, y, z] becomes P'[x’ ,y’ ,z’].
![Rendered by QuickLaTeX.com \hspace{4.5cm} \Large P'[x\,\,y\,\,z\,\,1]=P[x\,\,y\,\,z\,\,1].R_{yz}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fa9e86af44a9e19e131dc185102625af_l3.png)
3. Reflection along the X-Z plane: This is shown in the following figure –
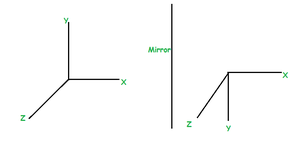
Reflection along the X-Z plane:
The Reflection transformation matrix for z-x axes is as follows:
![Rendered by QuickLaTeX.com \hspace{4.5cm} \Large R_{zx} =\left[\begin{matrix}1&0&0&0\\ 0&-1&0&0\\ 0&0&1&0\\0&0&0&1\end{matrix}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ffe072644c92416743683e799c043411_l3.png)
Consider, a point P[x, y, z] which is in 3D space is made to reflect along Z-X direction, after reflection P[x, y, z] becomes P'[x’, y’, z’].
![Rendered by QuickLaTeX.com \hspace{4.5cm} \Large P'[x\,\,y\,\,z\,\,1]=P[x\,\,y\,\,z\,\,1].R_{zx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a3e8b10d0b3fc9c8b09a8df80c821f6_l3.png)
Consider a cube ‘OABCDEFG’, which is given below, perform reflect transformation over it along X-Y plane.
The given cube is as follows:
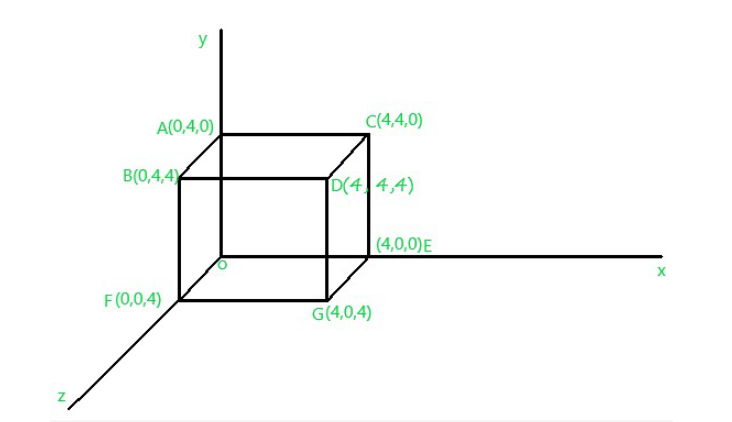
Fig.1
So, Matrix representation condition of Reflection transformation along X-Y axis:
![Rendered by QuickLaTeX.com \hspace{4.5cm} \Large R_{xy} =\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-81246286fa513459baa020f8f91b203f_l3.png)
Point O[0 0 0] becomes O’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large O'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]} \\ \hspace{6.68cm}\Large \mathbf{=[0\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]}\\ \hspace{4.37cm}\mathbf{O'[x ,y ,z]=[0 ,0 ,0]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e1a0756bc854aad21b7551325fac9ddb_l3.png)
Point A[0 4 0] becomes A’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large A'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[0\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]}\\ \hspace{6.68cm}\Large\mathbf{=[0\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}1]}\\ \hspace{4.37cm}\Large\mathbf{A'[x ,y ,z]=[0 ,4 ,0]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d32d961286a0567b8584d45dc6ec8fae_l3.png)
Point B[0 4 4] becomes B’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large B'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[0\hspace{0.2cm}4\hspace{0.2cm}4\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]}\\ \hspace{6.68cm}\Large\mathbf{=[0\hspace{0.2cm}4\hspace{0.2cm}4\hspace{0.2cm}1]} \newline \hspace{4.37cm}\Large\mathbf{B'[x ,y ,z]=[0 ,4 ,4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-565965f440f3f87859f95c91b64165da_l3.png)
Point C[-4 4 0] becomes C’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large C'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[4\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]}\\ \hspace{6.68cm} \Large \mathbf{=[-4\hspace{0.2cm}4\hspace{0.2cm}0\hspace{0.2cm}1]}\\ \newline \hspace{4.37cm}\Large\mathbf{C'[x ,y ,z]=[-4 ,4 ,0]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9b5e158171724159c3c87ba3e42ccb8b_l3.png)
Point D[4 4 4] becomes D’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large D'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[4\hspace{0.2cm}4\hspace{0.2cm}4\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]}\\ \hspace{6.68cm}\Large \mathbf{=[-4\hspace{0.2cm}4\hspace{0.2cm}4\hspace{0.2cm}1]}\\ \hspace{4.37cm}\Large\mathbf{D'[x ,y ,z]=[-4 ,4 ,4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d92fbd92710131c268ab79196e473602_l3.png)
Point E[4 0 0] becomes E’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large E'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[4\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]}\\ \hspace{6.68cm} \Large\mathbf{=[-4\hspace{0.2cm}0\hspace{0.2cm}0\hspace{0.2cm}1]}\\ \hspace{4.37cm}\mathbf{E'[x ,y ,z]=[-4 ,0 ,0]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-16db04e191b254be36ea4f5e324d9390_l3.png)
Point F[0 0 4] becomes F’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large F'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[0\hspace{0.2cm}0\hspace{0.2cm}4\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]}\\ \hspace{6.68cm}\Large \mathbf{=[0\hspace{0.2cm}0\hspace{0.2cm}4\hspace{0.2cm}1]}\\ \hspace{4.37cm}\mathbf{F'[x ,y ,z]=[0 ,0 ,4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0dfe5db7fa1331ac35a01e008c147662_l3.png)
Point G[4 0 4] becomes G’ after performing Reflection transformation:
![Rendered by QuickLaTeX.com \hspace{4cm} \mathbf{\Large G'[x\hspace{0.2cm}y\hspace{0.2cm}z\hspace{0.2cm}1]=[4\hspace{0.2cm}0\hspace{0.2cm}4\hspace{0.2cm}\hspace{0.2cm}1]\left[\begin{matrix}1&0&0&0\\ 0&1&0&0\\ 0&0&-1&0\\0&0&0&1\end{matrix}\right]}\\ \hspace{6.68cm}\Large \mathbf{=[-4\hspace{0.2cm}0\hspace{0.2cm}4\hspace{0.2cm}1]}\\ \newline \hspace{4.37cm}\mathbf{G'[x ,y ,z]=[-4 ,0 ,4]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-64cce2512bd513670a159f2ba723665f_l3.png)
After performing Reflection Transformation over the above figure (Fig.1) would look like:
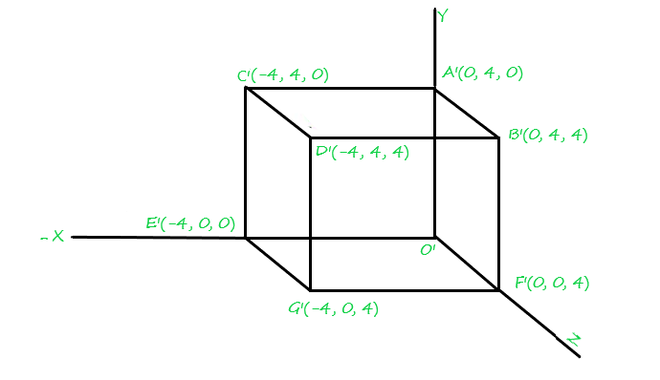
Reflected 3D image
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...