Compounding is a process of re-investing the earnings in your principal to get an exponential return as the coming next growth is on a bigger principal, following this process of adding earnings to the principal. In this passage of time, the principal will grow exponentially and produce unusual returns.
Sometimes we come across some statements like “one year interest for FD in the bank @ 11 % per annum.” or “Savings account with interest @ 8% per annum”. When it comes to investment, there are usually two types of interests :
- Simple Interest
- Compound Interest
We already know about Simple Interest(S.I), we will look at Compound Interest(C.I) in detail in this article. First, let’s understand what is compounding through a story.
A Prisoner was once awaiting his death sentence when the king asked for his last wish.
The Prisoner demanded grain of rice (foolish demand right?) but added that the number of grain should be doubled after moving to every square till the last square of the Chess Board ( that is 1 on first, 2 on second, 4 on third, 8 on fourth, 16 on fifth and so on, till the 64th square).
The king thought that it is a very small demand and ordered his ministers to have that much amount of rice calculated and provided to the prisoner. The amount calculated was so big that the king lost his entire kingdom and was indebted to prisoner all of his life.
What the prisoner used was the idea of “Compounding“. Now, let’s define Compound Interest.
Compound Interest
Compound interest (or compounding interest) is the interest on a loan or deposit calculated based on both the initial principal and the accumulated interest from previous periods. Thought to have originated in 17th-century Italy, compound interest can be thought of as “interest on interest,” and will make a sum grow at a faster rate than simple interest, which is calculated only on the principal amount.
Let’s see an example before working out the formula,
Question: Hema borrowed a sum of Rs. 2,00,000 for 2 years at an interest of 8% compounded annually from a bank. Find the Compound Interest and the amount she had to pay at the end of 2 years.
Answer:
To do it, we need to find interest year by year.
Step 1. First let’s find Simple Interest for the first year,
Here, principal P1 = 2,00,000, R = 8% and T = 1.
SI1 = SI at 8% on P1 for one year = 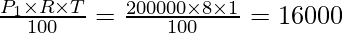
Step 2. So, now the amount received at the end of the first year = SI1 + P1 = 16000 + 2,00,000 = 2,16,000. Now, this will become principal.
Thus, P2 = 2,16,000, R = 8 and T = 1
Step 3. Now we will find simple interest for the second year by taking the total amount at the end of 1st year as principal P2.
SI2 = SI at 8% on P2 for one year =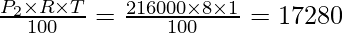
This amount now at the end of 2nd year = SI2 + P2 = 17280 + 2,16,000 = 2,33,280
Total interest given = 17280 + 16000 = 33280.,
We need to notice that Principal remains the same in Simple Interest(SI), but in Compound Interest(CI) it recalculated and changes every year.
Formula for Compound Interest
Let’s derive the formula for compound interest by taking the previous example only, but this time we will not use the values for the variables.
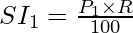
Now, the amount at the end of first year will the principal for the second year, i.e
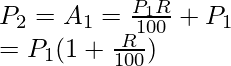
So, now SI for 2nd year
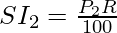
Calculating the amount for the 2nd year,
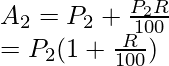
Now using the value of P2 in the above equation,
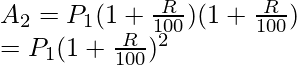
Similar if we keep calculating for “n” years,
We’ll end up with this formula of amount
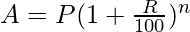
where P is the initial principal amount, R is the rate and n is the number of years after which the amount is calculated.
Rate Compounded Annually or Half Yearly
You may notice that, in the beginning, we used “rate compounded yearly”. What does it mean?
It means that interest was compounded once a year. We can also have our interest compounded half-yearly or quarterly. What happens in such cases?
Let’s compare the two cases through an example to see the difference between rates compounded yearly and half-yearly.
Suppose P = 1000, R = 5% and n = 2 years,
Case 1: Interest compound annually.
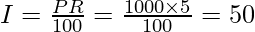
A = 50 + 1000 = 1050.
Case 2: Interest Compounded Half-Yearly.
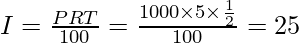
P2 = I + P = 1025
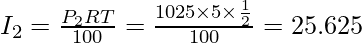
Final amount in this case A = P2 + I2 = 1025 + 25.625 = 1050.625
We can that if interest is compounded half-yearly, compute the interest two times. So the time period becomes twice and the rate is taken half.
So the formula becomes,
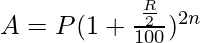
Applications of Compound Interest Formula and Examples
Growth and Decay
The compound interest concept can be applied to any quantity which increases or decreases such that the amount at the end of each period bears a constant ratio to the amount at the beginning of that period.
Let’s say, if the population of a town increases steadily by 2% p.a. of the population at the beginning each year, the yearly growth factor is 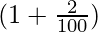 i.e., 1.02, and the population after n years is (1.02)n times population at the beginning of that period. If the population decreases by 2%, then the yearly decay factor is
i.e., 1.02, and the population after n years is (1.02)n times population at the beginning of that period. If the population decreases by 2%, then the yearly decay factor is 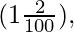 i.e., 0.98.
i.e., 0.98.
Question: The population of a town increases at the rate of 2.5% annually. If its present population is 3,26,40,000, find the population after 3 years.
Answer:
We can apply compound interest formula here,
Population “P” at the end of 3 years will be,

Appreciation and Depreciation
When the value of an article increases with the passage of time, the article is said to appreciate. When the value of an article decreases with the passage of time, the article is said to depreciate.
For example, if a man buys a car and uses it for two years, it is obvious that the car will not be worth it as a new one. The car will thus have depreciated in value. On the other hand, if a man buys a piece of land, he will probably find that in a few years he will be able to get a better price for it than the price he paid for it. The value of the land will thus have appreciated. When things are difficult to obtain, they have a rarity value and appreciation.
Question: The value of a residential flat constructed at a cost of Rs 10,00,000 is appreciating at the rate of 10% per year annum. What will be its value 3 years after construction?
Answer:
Value of flat P = 1000000, rate of appreciation = 10, n = 3
After 3 years, let the value of flat be “A”.
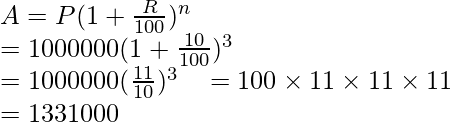
So, after 3 years value of flat will be 13,31,000.
The growth of a bacteria if the rate of growth is known:
Question: In a certain experiment, the count of bacteria was increasing at the rate of 2.5% per hour. Initially, the count was 51,20,000. Find the bacteria at the end of 2 hours.
Answer:
Initial count of bacteria = P = 51,20,000,
Increase rate “r” = 2.5 per hour,
We want to find the count after 2 hours, i.e; n = 2
Let the final count be “A”
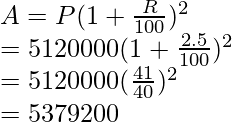
So, the final count of bacteria is 53,79,200.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...