Compositorial of a number

Given a natural number N, the task is to find the N^th compositorial number. 

Compositorial of a number refers to the product of all the positive composite integers up to N. 
The compositorial of a number N is denoted by 

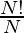
where N! is the factorial of the number and N# is the Primorial of the number N. 

Examples:

Input: N = 4 
Output: 1728 
Explanation:
The first 4 composite numbers are 4, 6, 8, 9. Therefore, the compositorial is the product of all the numbers. 
Input: N = 5 
Output: 17280 

Approach: The following steps can be followed to compute the N^th compositorial number.  

1. Get the number N.
2. Find all the composite numbers up to N.
3. Product the obtained composite numbers.
4. Print the product.

Below is the implementation of the above approach: 

C++

// C++ program to find compositorial
// of composite numbers
#include <bits/stdc++.h>
using namespace std;

vector<int> compo;

// Function to check if
// a number is composite.
bool isComposite(int n)
{

    // Corner cases
    if (n <= 3)
        return false;

    // This is checked so that we can
    // skip the middle five numbers
    // in the below loop
    if (n % 2 == 0 or n % 3 == 0)
        return true;

    int i = 5;
    while(i * i <= n)
    {
        if (n % i == 0 or
            n % (i + 2) == 0)
            return true;
        i = i + 6;
    }
    return false;
}

// This function stores all
// composite numbers less than N
void Compositorial_list(int n)
{
    int l = 0;
    for(int i = 4; i < 1000000; i++)
    {
       if (l < n)
       {
           if (isComposite(i))
           {
               compo.push_back(i);
               l += 1;
           }
       }
    }
}

// Function to calculate
// the compositorial of n
int calculateCompositorial(int n)
{

    // Multiply first n composite number
    int result = 1;

    for(int i = 0; i < n; i++)
        result = result * compo[i];
    return result;
}

// Driver code
int main()
{
    int n = 5;

    // Vector to store all the
    // composite less than N
    Compositorial_list(n);

    cout << (calculateCompositorial(n));

    return 0;
}

// This code is contributed by mohit kumar 29

Java

// Java program to find compositorial
// of composite numbers
import java.util.*;
class GFG{

static Vector<Integer> compo =
              new Vector<Integer>();

// Function to check if
// a number is composite.
static boolean isComposite(int n)
{
  // Corner cases
  if (n <= 3)
    return false;

  // This is checked so that we can
  // skip the middle five numbers
  // in the below loop
  if (n % 2 == 0 || n % 3 == 0)
    return true;

  int i = 5;
  while(i * i <= n)
  {
    if (n % i == 0 ||
        n % (i + 2) == 0)
      return true;
    i = i + 6;
  }
  return false;
}

// This function stores all
// composite numbers less than N
static void Compositorial_list(int n)
{
  int l = 0;
  for(int i = 4; i < 1000000; i++)
  {
    if (l < n)
    {
      if (isComposite(i))
      {
        compo.add(i);
        l += 1;
      }
    }
  }
}

// Function to calculate
// the compositorial of n
static int calculateCompositorial(int n)
{
  // Multiply first n
  // composite number
  int result = 1;

  for(int i = 0; i < n; i++)
    result = result * compo.get(i);
  return result;
}

// Driver code
public static void main(String[] args)
{
  int n = 5;

  // Vector to store all the
  // composite less than N
  Compositorial_list(n);

  System.out.print((calculateCompositorial(n)));
}
}

// This code is contributed by Princi Singh

Python3

# Python3 program to find Compositorial
# of composite numbers

# Function to check
# if a number is composite.
def isComposite(n):

    # Corner cases
    if (n <= 3):
        return False

    # This is checked so that we can
    # skip the middle five numbers
    # in the below loop
    if (n % 2 == 0 or n % 3 == 0):
        return True

    i = 5
    while(i * i <= n):

        if (n % i == 0\
            or n % (i + 2) == 0):
            return True
        i = i + 6

    return False

# This function stores all
# Composite numbers less than N
def Compositorial_list(n):
    l = 0
    for i in range(4, 10**6):
        if l<n:
            if isComposite(i):
                compo.append(i)
                l+= 1


# Function to calculate the
# Compositorial of n
def calculateCompositorial(n):

    # Multiply first n composite number
    result = 1
    for i in range(n):
        result = result * compo[i]
    return result

# Driver code
if __name__ == "__main__":
    n = 5

    # Vector to store all the
    # composite less than N
    compo =[]

    Compositorial_list(n)

    print(calculateCompositorial(n))

C#

// C# program to find compositorial
// of composite numbers
using System;
using System.Collections.Generic;
class GFG{

static List<int> compo =
            new List<int>();

// Function to check if
// a number is composite.
static bool isComposite(int n)
{
  // Corner cases
  if (n <= 3)
    return false;

  // This is checked so that we can
  // skip the middle five numbers
  // in the below loop
  if (n % 2 == 0 || n % 3 == 0)
    return true;

  int i = 5;
  while(i * i <= n)
  {
    if (n % i == 0 ||
        n % (i + 2) == 0)
      return true;
    i = i + 6;
  }
  return false;
}

// This function stores all
// composite numbers less than N
static void Compositorial_list(int n)
{
  int l = 0;
  for(int i = 4; i < 1000000; i++)
  {
    if (l < n)
    {
      if (isComposite(i))
      {
        compo.Add(i);
        l += 1;
      }
    }
  }
}

// Function to calculate
// the compositorial of n
static int calculateCompositorial(int n)
{
  // Multiply first n
  // composite number
  int result = 1;

  for(int i = 0; i < n; i++)
    result = result * compo[i];
  return result;
}

// Driver code
public static void Main(String[] args)
{
  int n = 5;

  // List to store all the
  // composite less than N
  Compositorial_list(n);

  Console.Write((calculateCompositorial(n)));
}
}

// This code is contributed by Rajput-Ji

Javascript

<script>
    // Javascript program to find compositorial
    // of composite numbers
    let compo = [];

    // Function to check if
    // a number is composite.
    function isComposite(n)
    {

        // Corner cases
        if (n <= 3)
            return false;

        // This is checked so that we can
        // skip the middle five numbers
        // in the below loop
        if (n % 2 == 0 || n % 3 == 0)
            return true;
        let i = 5;
        while(i * i <= n)
        {
            if (n % i == 0 ||
                n % (i + 2) == 0)
                return true;
            i = i + 6;
        }
        return false;
    }

    // This function stores all
    // composite numbers less than N
    function Compositorial_list(n)
    {
        let l = 0;
        for(let i = 4; i < 1000000; i++)
        {
           if (l < n)
           {
               if (isComposite(i))
               {
                   compo.push(i);
                   l += 1;
               }
           }
        }
    }

    // Function to calculate
    // the compositorial of n
    function calculateCompositorial(n)
    {

        // Multiply first n composite number
        let result = 1;

        for(let i = 0; i < n; i++)
            result = result * compo[i];
        return result;
    }

    let n = 5;

    // Vector to store all the
    // composite less than N
    Compositorial_list(n);
    document.write(calculateCompositorial(n));

// This code is contributed by divyeshrabadiya07.
</script>

Output:

17280