Time and Space Complexity Analysis of Binary Search Algorithm
Last Updated :
18 Mar, 2024
Time complexity of Binary Search is O(log n), where n is the number of elements in the array. It divides the array in half at each step. Space complexity is O(1) as it uses a constant amount of extra space.
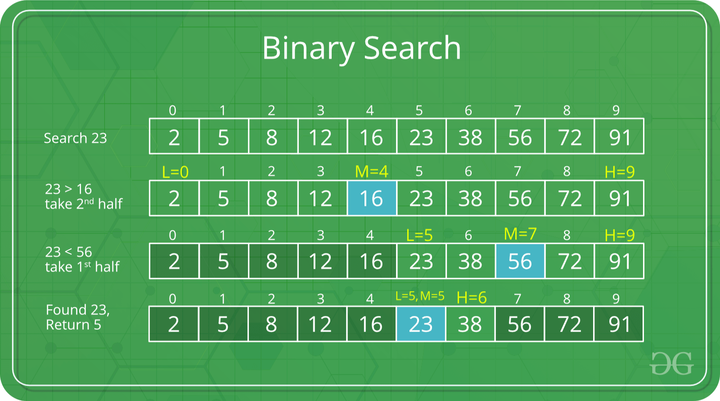
Example of Binary Search Algorithm
| Aspect |
Complexity |
| Time Complexity |
O(log n) |
| Space Complexity |
O(1) |
The time and space complexities of the binary search algorithm are mentioned below.
Best Case Time Complexity of Binary Search Algorithm: O(1)
Best case is when the element is at the middle index of the array. It takes only one comparison to find the target element. So the best case complexity is O(1).
Average Case Time Complexity of Binary Search Algorithm: O(log N)
Consider array arr[] of length N and element X to be found. There can be two cases:
- Case1: Element is present in the array
- Case2: Element is not present in the array.
There are N Case1 and 1 Case2. So total number of cases = N+1. Now notice the following:
- An element at index N/2 can be found in 1 comparison
- Elements at index N/4 and 3N/4 can be found in 2 comparisons.
- Elements at indices N/8, 3N/8, 5N/8 and 7N/8 can be found in 3 comparisons and so on.
Based on this we can conclude that elements that require:
- 1 comparison = 1
- 2 comparisons = 2
- 3 comparisons = 4
- x comparisons = 2x-1 where x belongs to the range [1, logN] because maximum comparisons = maximum time N can be halved = maximum comparisons to reach 1st element = logN.
So, total comparisons
= 1*(elements requiring 1 comparisons) + 2*(elements requiring 2 comparisons) + . . . + logN*(elements requiring logN comparisons)
= 1*1 + 2*2 + 3*4 + . . . + logN * (2logN-1)
= 2logN * (logN – 1) + 1
= N * (logN – 1) + 1
Total number of cases = N+1.
Therefore, the average complexity = (N*(logN – 1) + 1)/N+1 = N*logN / (N+1) + 1/(N+1). Here the dominant term is N*logN/(N+1) which is approximately logN. So the average case complexity is O(logN)
Worst Case Time Complexity of Binary Search Algorithm: O(log N)
The worst case will be when the element is present in the first position. As seen in the average case, the comparison required to reach the first element is logN. So the time complexity for the worst case is O(logN).
Auxiliary Space Complexity of Binary Search Algorithm
The auxiliary space complexity of the Binary Search Algorithm is O(1), which means it requires a constant amount of extra space regardless of the size of the input array. This is because Binary Search is an iterative algorithm that does not require any additional data structures or recursion that grows with the input size. Although, we can also implement Binary Search recursively.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...