Complex Integration

Last Updated : 01 May, 2023

Complex integration is a simple extension of the ideas we develop in calculus to the complex world. In real calculus, differentiation and integration are, roughly speaking, inverse operations (save for the additional interpretation of derivative as the slope of a function and integral as the area under the curve). We will see that the same inverse relationship between differentiation and integration exists in the complex domain; but in addition, differentiation and integration are also roughly equivalent operations. But to see this striking result, we have to wait till Cauchy’s Theorem. This article grows over the basics and is necessary for preparation for fully appreciating Cauchy’s Theorem and its results.

Complex integration of a real variable

Start with the basic, that is, for a complex function of a real variable, and then slowly ramp up to more complicated, yet exciting, cases of complex integration. Suppose that f is a complex-valued function of a real variable t. We can write f(t) = u(t) + iv(t), where u and v are now real-valued functions of a real variable. We can therefore define the integral of f(t) on the interval [a, b] as

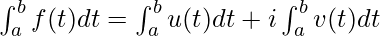$\int_{a}^{b}f(t)dt=\int_{a}^{b}u(t)dt+i\int_{a}^{b}v(t)dt$ , f(t) is integrable is it is continuous (Flashback to integration in real calculus), and for that matter, if u(t) and v(t) are continuous. We can clearly see that here f(t) is just a linear combination of u(t) and v(t). Hence all theorems and rules we know for real integration flow directly to this case.

Example 1: Integrate f(t) = 2t + it². Here, u(t) = 2t and v(t) = t². So, for 0≤t≤1.

Solution:

$\int_{0}^{1}f(t)dt=\int_{0}^{1}(2t+it^{2})dt=2\int_{0}^{1}tdt+i\int_{0}^{1}t^{2}dt=1+\frac{i}{3}$

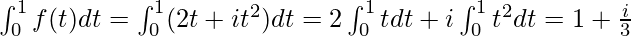
Example 2: Solve f(t) = ie^t. Integrating it from 0 to 2.

Solution:

$\int_{0}^{2}f(t)dt=\int_{0}^{2}ie^{t}dt=i(e^{2}-1)$

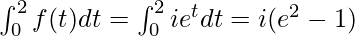
Contour Integrals

Contour integrals is basically the integration of the form, 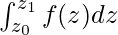$\int_{z_{0}}^{z_{1}}f(z)dz$

Where z₀ and z₁ are complex numbers. We immediately see a difficulty. Unlike the case of an interval [a, b] where it is obvious how to go from a to b, here we have points in the complex plane and there are infinitely many ways to go from one point to the other since the complex plane is a 2-dimensional plane. Therefore, the above integral is ambiguous. To do this integration, we have to define a path from z_oto z₁. This is similar to line integrals of vector functions in 3-dimensional space, where we need a specific parameterized path to compute the integral.

Definition: Let z₀ and z₁ be two points in the complex plane. A parameterized curve joining z₀ and z₁ can be defined by a continuous function z: [t₀, t₁] → C such that z(t₀) = z₀ and z(t₁) = z₁. We can think of t here as time. At any given instant in time t₀ ≤ t ≤ t₁, the particle is at the point z(t) in the complex plane. Therefore we see that a curve joining z₀ and z₁ can be defined by a function z(t) mapping points t-domain, in the interval [t₀, t₁], to corresponding points z(t) in the complex plane, such that z(t₀) = z₀ and z(t₁) = z₁. As an immediate result of this definition, we can decompose z into its real and imaginary parts, and this is equivalent to two continuous real-valued functions x(t) and y(t) defined on the interval [t₀, t₁] such that x(t₀) = x₀ and x(t₁) = x₁ and similarly for y(t): y(t₀) = y₀ and y(t₁) = y₁, where z₀ = x₀ + iy₀ and z₁ = x₁ + iy₁. We call the curve smooth if its velocity dz(t)/dt = z'(t) is a continuous function in the interval [t₀, t₁] which is never zero.

Let Γ be a smooth parameterized curve joining z₀ to z₁, and let f(z) be a complex-valued function that is continuous on Γ. Then we define the integral of f along Γ by,

$\int_{\Gamma }^{}f(z)dz=\int_{t_{0}}^{t_{1}}f(z(t))z'(t)dt$

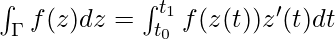
The complex integral also satisfies some properties like linearity and change of sign when integrated into the reverse direction. The proofs of these properties are easy and can be easily done by using the definition.

Linearity property

∫_Γ(αf(z) + βg(z))dz = α∫_Γf(z)dz + β∫_Γg(z))dz

Sign reversal property

∫_−Γf(z)dz = −∫_Γf(z)dz

Example 1: Consider the function f(z) = |z|² = x² + y²integrated along the curve parameterized by z(t) = t + it for 0 ≤ t ≤ 1.

Solution:

This is the straight line segment joining the origin and the point 1+ i. We have here ̇dz(t)/dt = z'(t) = 1 + i. So,

$\int_{path}^{}f(z)z'(t)dt = \int_{0}^{1}(t^{2}+t^{2})(1+i)dt=2(1+i)\int_{0}^{1}t^{2}dt=\frac{2}{3}(1+i)$

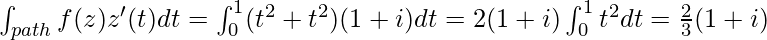
Example 2: Consider now the function f(z) = 1/z integrated along the smooth curve Γ parameterized by z(θ) = R e^{(i θ)} for 0 ≤ θ ≤ 2π, where R ≠ 0.

Solution:

The curve is a circle of radius R centered about the origin. Here f(z(θ)) = (1/R) e^{(−i θ)} and dz(θ)/dθ = z'(θ) = i R e^{(i θ)} = iz. So, we have:

$\int_{path}^{}f(z)z'(θ)dθ=\int_{0}^{2\pi }\frac{1}{z}izdθ=i\int_{0}^{2\pi }dθ = 2\pi i$

Note that the result is independent of R.

Example 3: Compute the integral of ln(z) over the unit circle |z| = 1. Parameterized z = e^iθ.

Solution:

So, considering 0 ≤ θ ≤ 2π. Here we took |z| = 1 as it is specified. Now, dz(θ)/dθ = z'(θ) = ie^iθ.

$\int_{|z|=1}^{}f(z)z'(\theta )d\theta = \int_{0}^{2\pi }ln(e^{i\theta })ie^{i\theta }d\theta = -\int_{0}^{2\pi }\theta e^{i\theta }d\theta$

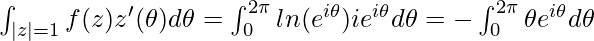
After doing integration by parts, we finally get 2πi.

Results from Contour Integration

Result 1: Take f(z) = 1, then according to the above definition,

$\int_{\Gamma }^{}f(z)dz=\int_{t_{0}}^{t_{1}}z'(t)dt$

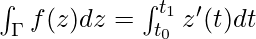
Result 2: The length of the curve is the contour integral of the modulus of dz, the real function |dz|. The length of the curve Γ is, therefore,

$\int_{\Gamma }^{}|dz|=\int_{t_{0}}^{t_{1}}|z'(t)|dt=\int_{t_{0}}^{t_{1}}\sqrt{x'(t)^{2}+y'(t)^{2}}dt$

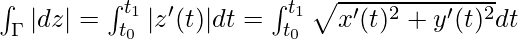
Result 3: Estimating the maximum value of a contour integral.

$|\int_{\Gamma }^{}f(z)dz|=|\int_{t_{0}}^{t_{1}}f(z(t))z'(t)dt|\leq \int_{t_{0}}^{t_{1}}|f(z(t))||z'(t)|dt\leq max_{z\subseteq \Gamma }|f(z)| \int_{t_{0}}^{t_{1}}|z'(t)|dt$

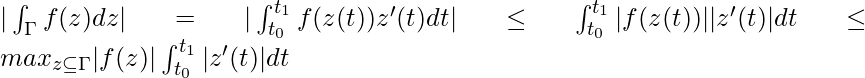
Piecewise-smooth curve

If Γ₁ is a smooth curve joining z₀ to z₁ and Γ₂ is another smooth curve joining z₁ to z₂, then we can make a curve Γ, not necessarily smooth, by joining z₀ to z₂ by first going to the intermediate point z₁ via Γ₁ and then from there via Γ₂ to our destination z₂. The resulting curve Γ is still continuous, but it may not be smooth, since the velocity need not be continuous at the intermediate point z₁. Such curves can be called piecewise smooth or contours, as popularly called in the literature. We can, thus, construct curves that are not smooth but which can be made out of a finite number of smooth curves, called smooth components.

Let Γ be a contour with n smooth components {Γ_j} for j = 1, 2, . . . , n. If f(z) is a function continuous on Γ, then the contour integral of f along Γ is defined as

$\int_{\Gamma }^{}f(z)dz=\sum_{j=1}^{n}\int_{\Gamma _{j}}^{}f(z)dz =\int_{\Gamma _{1}}^{}f(z)dz+\int_{\Gamma _{2}}^{}f(z)dz+....+\int_{\Gamma _{n}}^{}f(z)dz$

Example 1: Find the upper bound of the integral I =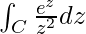 $\int_{C}^{}\frac{e^{z}}{z^{2}}dz$ , where C is the straight line joining points (0,1) and (2,0).

Solution:

First task is to find |f(z)|. This is: |f(z)| = 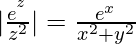$|\frac{e^{^{z}}}{z^{2}}|=\frac{e^{x}}{x^{2}+y^{2}}$

Line C is shown here. Equation of C is 2y + x – 2 = 0.

Here, on the line C, |f(z)| becomes a function of one variable. Putting y = (2 – x)/2, we get,

$|f(z)| = \frac{e^{x}}{x^{2}+(\frac{2-x}{2})^{2}}$

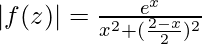
The maximum value attained by |f(z)| is e^4/5 at x = 4/5.

Now the length of the contour C is basically the distance between (0,1) and (2,0), that is, √5.

Using Result-3, we have I ≤ √5e^4/5

Example 2: Integrate f(z) = |z|² again, but over piecewise smooth contour.

Solution:

Break the whole integration process into four parts.

For OA, dy = 0. So dz = dx. y = 0, so |z|² = x².

For AB, dx = 0. So dz = idy. x = 1 so |z|² = 1+y².

For BC, dy = 0, So dz = dx. y = 1 so |z|² = x²+1.

For CO, dx = 0, so dz = idy. x = 0, so |z|² = y².

$\oint_{C}^{}|z|^{2}dz=\int_{0}^{1}x^{2}dx+i\int_{0}^{1}(1+y^{2})dy+\int_{1}^{0}(1+x^{2})dx+i\int_{1}^{0}y^{2}dy =\frac{1}{3}+\frac{4i}{3}-\frac{4}{3}-\frac{i}{3}=-1+i$

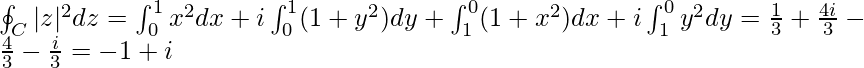
Path Independence Theorem

In vector calculus, the line integral becomes independent of the path in some special cases. This happens when the vector function can be expressed as the gradient of a scalar function. Similar is the notion of independence of path in complex integration. If we have a function whose anti-derivative exists in a region, we can say that the integral of the function will be independent of the path of integration. A domain is a subset (or a region) of a complex plane, in which every pair of points can be connected via a contour (or a piecewise-smooth curve).

Let D be a domain and let f: D → C be a continuous complex-valued function defined on D. We say that f has an antiderivative in D if there exists some function F: D → C such that,

F'(z) = 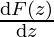$\frac{\mathrm{d}F(z) }{\mathrm{d} z}$ = f(z)

Clearly, F is analytic in D. Let Γ be any contour in D with endpoints z₀ and z₁. If f has an antiderivative F on D, the contour integral is given by, ∫_Γf(z)dz = F(z₁) − F(z₀). The proof is straightforward. Start with the definition and parameterize Γ by z(t) for 0 ≤ t ≤ 1. Then,

$\int_{\Gamma }^{}f(z)dz= \int_{0}^{1}F'(z(t))z'(t)dt=\int_{0}^{1}\frac{\mathrm{d} F(z(t))}{\mathrm{d} t} = F(z(1))-F(z(0))=F(z_{1})-F(z_{0})$

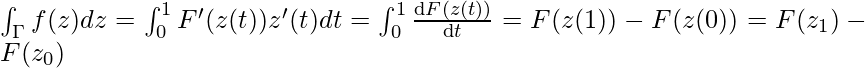
For a more general contour, we can segment the whole contour into individual smooth components {Γj} for j = 1, 2, . . . , n. Then, we can readily see that the end points of each smooth component cancel out, leaving behind the start and end points.

∫_Γf(z)dz =_{j = 1}∑ⁿ∫_Γjf(z)dz = ∫_Γ1f(z)dz + ∫_Γ2f(z)dz + …. + ∫_Γnf(z)dz = F(τ₁) − F(z₀) + F(τ₂) − F(τ₁)+….+F(z₁) − F(τ_n−1) = F(z₁) − F(z₀)

This result says that if a function f has an antiderivative, then its contour integrals do not depend on the precise path, but only on the endpoints. If we now have a closed contour, meaning the start and end points coincide, then the closed contour integral in such a case is zero. Explicitly stated, if Γ is a closed contour in some domain D and f : D → C has an antiderivative in D, then,

$\oint_{\Gamma }^{}f(z)dz=0$

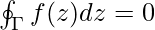
This is the precise mathematical statement of path independence of a complex function, whose anti-derivative exists in the given domain. For example, complex exponential and polynomials are functions whose anti-derivative exists and so their closed contour integrals are zero by the path-independence theorem.

Suggest improvement

Introduction to Complex Analysis

Share your thoughts in the comments