Complementation process in DFA

Prerequisite – Design a Finite automata
Suppose we have a DFA that is defined by ( Q, 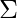, , 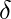q0, F ) and it accepts the language L₁. Then, the DFA which accepts the language L₂ where L₂ = ̅L₁‘, will be defined as below: 

( Q, 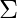, , q0, Q-F )

The complement of a DFA can be obtained by making the non-final states as final states and vice-versa. The language accepted by the complemented DFA L₂ is the complement of the language L₁. 

Example-1:
L₁: set of all strings over {a, b} of even length 

L1 = {, ab, aa, abaa, aaba, ....} 

L₂: set of all strings over {a, b} of odd length 

L2 = { a, b, aab, aaa, bba, bbb, ...} 

Here, we can see that L₂ = ̅L₁

Lets first draw the DFA for L₁ that accepts the strings of even length. 

Now, for designing the DFA for L₂, we just need to complement the above DFA. We will change the non-final states as final state and the final states as non-final states. 

This is our required complemented DFA. 

Example-2:
L₁: set of all strings over {a, b} starting with ‘a’. 

L1 ={ a, ab, aa, aba, aaa, aab, ..} 

L₂: set of all strings over {a, b} not starting with ‘a’. 

L2 ={ , b, ba, bb, bab, baa, bba, ...} 

Here, we can see that L₂ = ̅L₁

Lets first draw the DFA for L₁ that accepts the set of all strings over {a, b} starting with ‘a’ 

Now, for designing the DFA for L₂, we just need to complement the above DFA. We will change the non-final states as final state and the final states as non-final states. 

This is our required complemented DFA that accepts the strings that are not starting with ‘a’. 
Note: Regular languages are closed under complement (i.e Complement of regular language will also be regular).