Complement of a number with any base b
Last Updated :
01 Sep, 2022
In this post, a general method of finding complement with any arbitrary base 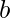 is discussed.
is discussed.
Remember: It is recommended to go through below as follows:
Steps to find (b-1)’s complement: To find (b-1)’s complement,
- Subtract each digit of the number from the largest number in the number system with base
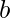 .
. - For example, if the number is a three-digit number in base 9, then subtract the number from 888 as 8 is the largest number in base 9 number system.
- The obtained result is the (b-1)’s (8’s complement) complement.
Steps to find b’s complement: To find b’s complement, just add 1 to the calculated (b-1)’s complement. Now, this holds true for any base in the number system that exists. It can be tested with familiar bases that is the 1’s and 2’s complement.
Example:
Let the number be 10111 base 2 (b=2)
Then, 1's complement will be 01000 (b-1)
2's complement will be 01001 (b)
Taking a number with Octal base:
Let the number be -456.
Then 7's complement will be 321
and 8's complement will be 322
Below is the implementation of the above idea as follows:
C++
#include <cmath>
#include <iostream>
using namespace std;
int prevComplement(int n, int b)
{
int maxDigit, maxNum = 0, digits = 0, num = n;
while (n != 0) {
digits++;
n = n / 10;
}
maxDigit = b - 1;
while (digits--) {
maxNum = maxNum * 10 + maxDigit;
}
return maxNum - num;
}
int complement(int n, int b)
{
return prevComplement(n, b) + 1;
}
int main()
{
cout << prevComplement(25, 7) << endl;
cout << complement(25, 7);
return 0;
}
|
Java
class GFG
{
static int prevComplement(int n, int b)
{
int maxDigit, maxNum = 0,
digits = 0, num = n;
while(n != 0)
{
digits++;
n = n / 10;
}
maxDigit = b - 1;
while((digits--) > 0)
{
maxNum = maxNum * 10 + maxDigit;
}
return maxNum - num;
}
static int complement(int n, int b)
{
return prevComplement(n, b) + 1;
}
public static void main(String args[])
{
System.out.println(prevComplement(25, 7));
System.out.println(complement(25, 7));
}
}
|
Python 3
def prevComplement(n, b) :
maxNum, digits, num = 0, 0, n
while n > 1 :
digits += 1
n = n // 10
maxDigit = b - 1
while digits :
maxNum = maxNum * 10 + maxDigit
digits -= 1
return maxNum - num
def complement(n, b) :
return prevComplement(n, b) + 1
if __name__ == "__main__" :
print(prevComplement(25, 7))
print(complement(25, 7))
|
C#
class GFG
{
static int prevComplement(int n, int b)
{
int maxDigit, maxNum = 0,
digits = 0, num = n;
while(n != 0)
{
digits++;
n = n / 10;
}
maxDigit = b - 1;
while((digits--) > 0)
{
maxNum = maxNum * 10 + maxDigit;
}
return maxNum - num;
}
static int complement(int n, int b)
{
return prevComplement(n, b) + 1;
}
public static void Main()
{
System.Console.WriteLine(prevComplement(25, 7));
System.Console.WriteLine(complement(25, 7));
}
}
|
PHP
<?php
function prevComplement($n, $b)
{
$maxNum = 0;
$digits = 0;
$num = $n;
while((int)$n != 0)
{
$digits++;
$n = $n / 10;
}
$maxDigit = $b - 1;
while($digits--)
{
$maxNum = $maxNum * 10 +
$maxDigit;
}
return $maxNum - $num;
}
function complement($n, $b)
{
return prevComplement($n, $b) + 1;
}
echo prevComplement(25, 7), "\n";
echo(complement(25, 7));
?>
|
Javascript
<script>
function prevComplement(n , b) {
var maxDigit, maxNum = 0, digits = 0,
num = n;
while (n != 0) {
digits++;
n = parseInt(n / 10);
}
maxDigit = b - 1;
while ((digits--) > 0) {
maxNum = maxNum * 10 + maxDigit;
}
return maxNum - num;
}
function complement(n , b) {
return prevComplement(n, b) + 1;
}
document.write(prevComplement(25, 7)+"<br/>");
document.write(complement(25, 7));
</script>
|
Time Complexity: O(log n)
Auxiliary Space: O(1)
Share your thoughts in the comments
Please Login to comment...