Comparison between Adjacency List and Adjacency Matrix representation of Graph
Last Updated :
08 Oct, 2021
A Graph is a non-linear data structure consisting of nodes and edges. The nodes are sometimes also referred to as vertices and the edges are lines or arcs that connect any two nodes in the graph. In this article, we will understand the difference between the ways of representation of the graph.
A graph can be represented in mainly two ways. They are:
- Adjacency List: An Adjacency list is an array consisting of the address of all the linked lists. The first node of the linked list represents the vertex and the remaining lists connected to this node represents the vertices to which this node is connected. This representation can also be used to represent a weighted graph. The linked list can slightly be changed to even store the weight of the edge.
- Adjacency Matrix: Adjacency Matrix is a 2D array of size V x V where V is the number of vertices in a graph. Let the 2D array be adj[][], a slot adj[i][j] = 1 indicates that there is an edge from vertex i to vertex j. Adjacency matrix for undirected graph is always symmetric. Adjacency Matrix is also used to represent weighted graphs. If adj[i][j] = w, then there is an edge from vertex i to vertex j with weight w.
Let us consider a graph to understand the adjacency list and adjacency matrix representation. Let the undirected graph be:
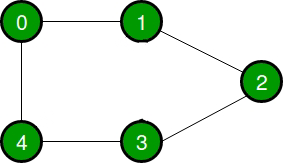
The following graph is represented in the above representations as:
- Adjacency Matrix: In the adjacency matrix representation, a graph is represented in the form of a two-dimensional array. The size of the array is V x V, where V is the set of vertices. The following image represents the adjacency matrix representation:

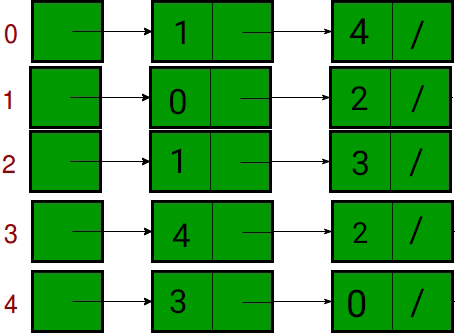
- Adjacency List: In the adjacency list representation, a graph is represented as an array of linked list. The index of the array represents a vertex and each element in its linked list represents the vertices that form an edge with the vertex. The following image represents the adjacency list representation:
The following table describes the difference between the adjacency matrix and the adjacency list:
| Operations |
Adjacency Matrix |
Adjacency List |
| Storage Space |
This representation makes use of VxV matrix, so space required in worst case is O(|V|2). |
In this representation, for every vertex we store its neighbours. In the worst case, if a graph is connected O(V) is required for a vertex and O(E) is required for storing neighbours corresponding to every vertex .Thus, overall space complexity is O(|V|+|E|). |
| Adding a vertex |
In order to add a new vertex to VxV matrix the storage must be increases to (|V|+1)2. To achieve this we need to copy the whole matrix. Therefore the complexity is O(|V|2). |
There are two pointers in adjacency list first points to the front node and the other one points to the rear node.Thus insertion of a vertex can be done directly in O(1) time. |
| Adding an edge |
To add an edge say from i to j, matrix[i][j] = 1 which requires O(1) time. |
Similar to insertion of vertex here also two pointers are used pointing to the rear and front of the list. Thus, an edge can be inserted in O(1)time. |
| Removing a vertex |
In order to remove a vertex from V*V matrix the storage must be decreased to |V|2 from (|V|+1)2. To achieve this we need to copy the whole matrix. Therefore the complexity is O(|V|2). |
In order to remove a vertex, we need to search for the vertex which will require O(|V|) time in worst case, after this we need to traverse the edges and in worst case it will require O(|E|) time.Hence, total time complexity is O(|V|+|E|). |
| Removing an edge |
To remove an edge say from i to j, matrix[i][j] = 0 which requires O(1) time. |
To remove an edge traversing through the edges is required and in worst case we need to traverse through all the edges.Thus, the time complexity is O(|E|). |
| Querying |
In order to find for an existing edge the content of matrix needs to be checked. Given two vertices say i and j matrix[i][j] can be checked in O(1) time. |
In an adjacency list every vertex is associated with a list of adjacent vertices. For a given graph, in order to check for an edge we need to check for vertices adjacent to given vertex. A vertex can have at most O(|V|) neighbours and in worst can we would have to check for every adjacent vertex. Therefore, time complexity is O(|V|) . |
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...