Combined Standard Deviation: Meaning, Formula, and Example
Last Updated :
06 Apr, 2023
A scientific measure of dispersion, which is widely used in statistical analysis of a given set of data is known as Standard Deviation. Another name for standard deviation is Root Mean Square Deviation. Standard Deviation is denoted by a Greek Symbol σ (sigma). Under this method, the deviation of values is taken from the arithmetic mean of the given set of data.
According to Spiegel, “The Standard Deviation is the square root of the arithmetic mean of the squares of all deviations. Deviations being measured from arithmetic mean of the items.”
Standard Deviation is considered to be the best way of determining the dispersion of a data set. It is because standard deviation takes into account every value of a data set along with its algebraic signs.
What is Combined Standard Deviation?
Calculating standard deviation of two or more series is known as Combined Standard Deviation. The formula of Combined Standard Deviation in the case of two series is:
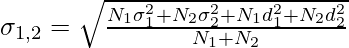
Where,
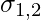 = Combined Standard Deviation of two groups
= Combined Standard Deviation of two groups
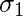 =Standard Deviation of first group
=Standard Deviation of first group
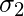 = Standard Deviation of second group
= Standard Deviation of second group
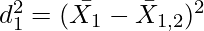
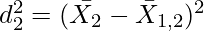
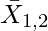 = Combined Arithmetic Mean of two groups
= Combined Arithmetic Mean of two groups
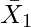 = Arithmetic Mean of first group
= Arithmetic Mean of first group
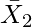 = Arithmetic Mean of second group
= Arithmetic Mean of second group
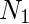 = Number of Observations in the first group
= Number of Observations in the first group
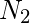 = Number of Observations in the second group
= Number of Observations in the second group
The formula of Combined Standard Deviation can be extended up to N number of series. For example, if there are three series, then the formula for Combined Standard Deviation will be:
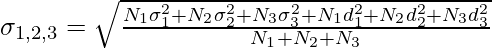
Where,
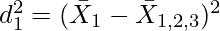
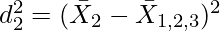
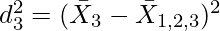
Example:
With the help of the following information, calculate Combined Standard Deviation.
Solution:
First of all, we have to calculate Combined Mean of the given two series.
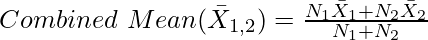
In the given question,
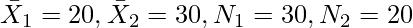
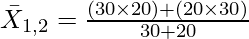
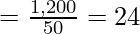
Combined Standard Deviation:
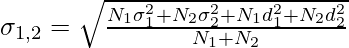
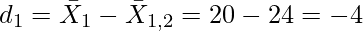
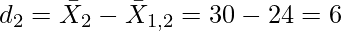
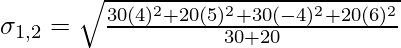
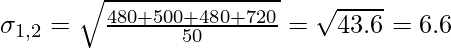
Combined Standard Deviation = 6.6
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...