Combinational circuits using Decoder
Last Updated :
15 May, 2023
Prerequisite- Binary Decoder, Multiplexers
A Decoder is a combinational circuit that converts binary information from 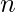 input lines to
input lines to 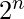 unique output lines. Apart from the Input lines, a decoder may also have an Enable input line.
unique output lines. Apart from the Input lines, a decoder may also have an Enable input line.
Decoder as a De-Multiplexer –
A Decoder with Enable input can function as a demultiplexer. A demultiplexer is a circuit that receives information from a single line and directs it to one of 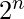 possible output lines.
possible output lines.
A 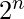 demultiplexer receives as input,
demultiplexer receives as input, 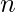 selection lines and one Input line. These selection lines are used to select one output line out of
selection lines and one Input line. These selection lines are used to select one output line out of 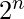 possible lines. To implement a
possible lines. To implement a 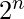 demultiplexer, we use a
demultiplexer, we use a 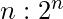 decoder with Enable input. The
decoder with Enable input. The 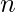 selection lines of the demultiplexer are the
selection lines of the demultiplexer are the 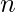 input lines that the decoder gets and the one input line of demultiplexer is the Enable input of the Decoder.
input lines that the decoder gets and the one input line of demultiplexer is the Enable input of the Decoder.
Making 1:4 demultiplexer using 2:4 Decoder with Enable input. Let A, B be the selection lines and EN be the input line for the demultiplexer.
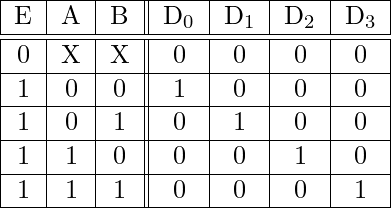
The decoder shown below functions as a 2:4 demultiplexer when EN is taken as a data input line and A and B are taken as the selection inputs. The single input variable E has a path to all four outputs, but the input information is directed to only one of the output lines, as specified by the binary combination of the two selection lines A and B. This can be verified from the truth table of the circuit.
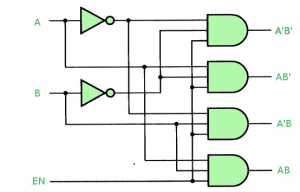
Truth Table-
Combinational Logic Implementation using Decoder –
A decoder takes 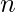 input lines and has
input lines and has 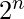 output lines. These output lines can provide the
output lines. These output lines can provide the 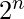 minterms of
minterms of 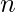 input variables.
input variables.
Since any boolean function can be expressed as a sum of minterms, a decoder that can generate these minterms along with external OR gates that form their logical sums, can be used to form a circuit of any boolean function.
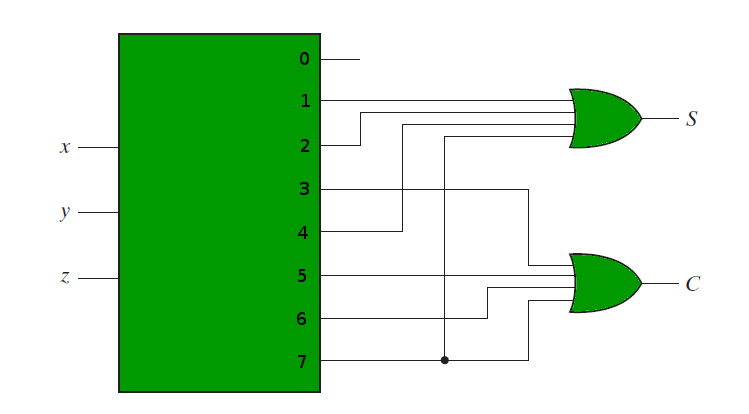
For example, if we need to implement the logic of a full adder, we need a 3:8 decoder and OR gates. The input to the full adder, first and second bits and carry bit, are used as input to the decoder. Let x, y and z represent these three bits. Sum and Carry outputs of a full adder have the following truth tables-

Therefore we have-
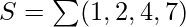
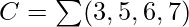
The following circuit diagram shows the implementation of Full adder using a 3:8 Decoder and OR gates.
Advantages and Disadvantages of Combinational circuits using Decoder:
Advantages of Combinational circuits using Decoder:
1.Simplification: Combinational circuits utilizing Decoder can improve on the plan of complicated advanced circuits by diminishing the quantity of information sources required and the intricacy of the rationale capabilities.
2.Flexibility: Combinational circuits utilizing Decoder can be utilized in a large number of utilizations since they can change over paired codes into one-hot codes that can be utilized to control other circuit parts like multiplexers, demultiplexers, or memory gadgets.
3.Modularity: Combinational circuits utilizing Decoder can be effectively scaled and coordinated into bigger computerized frameworks since they are secluded and can be flowed to make more perplexing circuits.
4.Reliability: Combinational circuits utilizing Decoder are dependable and have a low likelihood of failing since they are made out of straightforward, surely knew parts.
Disadvantages of Combinational circuits using Decoder:
1.Complexity: Combinational circuits utilizing Decoder can be complicated and require cautious plan to guarantee that the rationale capabilities are accurately executed and that there are no race conditions or errors.
2.Delay: Combinational circuits utilizing Decoder can bring delay into the circuit since the Decoder expects time to change over the information code into the one-hot result code.
3.Power utilization: Combinational circuits utilizing Decoder can consume more power than different sorts of circuits since they require various parts to carry out the rationale capabilities.
4.Limited adaptability: Combinational circuits utilizing Decoder are restricted to changing over parallel codes into one-hot codes, which can be a detriment in applications that require more mind boggling rationale works or backing for different kinds of codes.
References-
Digital Design, 5th edition by Morris Mano and Michael Ciletti
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...