Collision Course | TCS MockVita 2020
Last Updated :
21 Nov, 2022
Problem Description
On a busy road, multiple cars are passing by. A simulation is run to see what happens if brakes fail for all cars on the road. The only way for them to be safe is if they don’t collide and pass by each other. The goal is to identify whether any of the given cars would collide or pass by each other safely around a Roundabout. Think of this as a reference point O ( Origin with coordinates (0, 0) ), but instead of going around it, cars pass through it.
Considering that each car is moving in a straight line towards the origin with individual uniform speed. Cars will continue to travel in that same straight line even after crossing origin. Calculate the number of collisions that will happen in such a scenario.
Note: Calculate collisions only at origin. Ignore the other collisions. Assume that each car continues on its respective path even after the collision without change of direction or speed for an infinite distance.
Given an array car[] which contains the co-ordinates and their speed for each element. Find the total number of collisions at origin.
Example:
Input: car[] = {(5 12 1), (16 63 5), (-10 24 2), (7 24 2), (-24 7 2)}
Output: 4
Explanation:
Let the 5 cars be A, B, C, D, and E respectively.
4 Collisions are as follows –
A & B, A & C, B & C, D & E
Approach: The idea is to find the number of cars colliding at origin. We are given coordinate position of cars, from which we can find the distance of cars from origin.
Let x, y be position of a car then distance from origin will be:
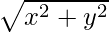
Dividing this distance with speed will give us time at which a car is present at origin. So if there are ‘N’ cars present at origin at some instant of time then total collisions will be
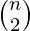
Adding all collision at a different instance of time will give our required answer.
Below is the implementation of the above approach:
C++
#include <bits/stdc++.h>
using namespace std;
struct Car {
long long x;
long long y;
long long v;
};
long long solve(long long c,
vector<Car>& arr)
{
map<long long, long long> freq;
long sum = 0;
for (long long i = 0; i < c; i++) {
long long x = arr[i].x,
y = arr[i].y,
v = arr[i].v;
long long dist_square
= (x * x) + (y * y);
long long time_square
= dist_square / (v * v);
freq[time_square]++;
}
for (auto it = freq.begin();
it != freq.end(); it++) {
long long f = it->second;
if (f <= 0)
continue;
sum += (f * (f - 1)) / 2;
}
return sum;
}
int main()
{
long long c = 5;
vector<Car> arr;
Car tmp;
tmp.x = 5;
tmp.y = 12;
tmp.v = 1;
arr.push_back(tmp);
tmp.x = 16;
tmp.y = 63;
tmp.v = 5;
arr.push_back(tmp);
tmp.x = -10;
tmp.y = 24;
tmp.v = 2;
arr.push_back(tmp);
tmp.x = 7;
tmp.y = 24;
tmp.v = 2;
arr.push_back(tmp);
tmp.x = -24;
tmp.y = 7;
tmp.v = 2;
arr.push_back(tmp);
cout << solve(c, arr);
return 0;
}
|
Java
import java.util.*;
class Car {
public int x;
public int y;
public int v;
public Car(int x, int y, int z)
{
this.x = x;
this.y = y;
this.v = z;
}
}
class GFG
{
static int solve(int c, ArrayList<Car> arr)
{
HashMap<Double, Integer> freq = new HashMap<Double, Integer>();
int sum = 0;
for (int i = 0; i < c; i++) {
int x = arr.get(i).x,
y = arr.get(i).y,
v = arr.get(i).v;
double dist_square
= (x * x) + (y * y);
double time_square
= dist_square / (v * v);
if (!freq.containsKey(time_square))
freq.put(time_square,0);
freq.put(time_square, freq.get(time_square) + 1);
}
for (var entry: freq.entrySet()) {
int f = entry.getValue();
if (f <= 0)
continue;
sum += (f * (f - 1)) / 2;
}
return sum;
}
public static void main(String[] args)
{
int c = 5;
ArrayList<Car> arr = new ArrayList<Car>();
arr.add(new Car(5, 12, 1));
arr.add(new Car(16, 63, 5));
arr.add(new Car(-10, 24, 2));
arr.add(new Car(7, 24, 2));
arr.add(new Car(-24, 7, 2));
System.out.println(solve(c, arr));
}
}
|
Python3
class Car :
def __init__(self, x, y, v):
self.x = x;
self.y = y;
self.v = v;
def solve(c, arr):
freq = {};
sums = 0;
for i in range(c):
x = arr[i].x
y = arr[i].y
v = arr[i].v;
dist_square = (x * x) + (y * y);
time_square = dist_square / (v * v);
if time_square not in freq:
freq[time_square] = 0;
freq[time_square]+=1;
for key in freq:
val = freq[key]
if (val <= 0):
continue;
sums += (val * (val- 1)) // 2;
return sums;
c = 5;
arr = [];
tmp = Car(5, 12, 1);
arr.append(tmp);
tmp = Car(16, 63, 5);
arr.append(tmp);
tmp = Car(-10, 24, 2);
arr.append(tmp);
tmp = Car(7, 24, 2);
arr.append(tmp);
tmp = Car(-24, 7, 2);
arr.append(tmp);
print(solve(c, arr));
|
C#
using System;
using System.Collections.Generic;
class Car {
public int x;
public int y;
public int v;
public Car(int x, int y, int z)
{
this.x = x;
this.y = y;
this.v = z;
}
}
class GFG
{
static int solve(int c,
List<Car> arr)
{
Dictionary<double, int> freq = new Dictionary<double, int>();
int sum = 0;
for (int i = 0; i < c; i++) {
int x = arr[i].x,
y = arr[i].y,
v = arr[i].v;
double dist_square
= (x * x) + (y * y);
double time_square
= dist_square / (v * v);
if (!freq.ContainsKey(time_square))
freq[time_square] = 0;
freq[time_square]++;
}
foreach (var entry in freq) {
int f = entry.Value;
if (f <= 0)
continue;
sum += (f * (f - 1)) / 2;
}
return sum;
}
public static void Main(string[] args)
{
int c = 5;
List<Car> arr = new List<Car>();
arr.Add(new Car(5, 12, 1));
arr.Add(new Car(16, 63, 5));
arr.Add(new Car(-10, 24, 2));
arr.Add(new Car(7, 24, 2));
arr.Add(new Car(-24, 7, 2));
Console.WriteLine(solve(c, arr));
}
}
|
Javascript
class Car {
constructor(x, y, v)
{
this.x = x;
this.y = y;
this.v = v;
}
};
function solve(c, arr)
{
let freq = {};
let sum = 0;
for (var i = 0; i < c; i++) {
var x = arr[i].x,
y = arr[i].y,
v = arr[i].v;
var dist_square
= (x * x) + (y * y);
var time_square
= dist_square / (v * v);
if (!freq.hasOwnProperty(time_square))
freq[time_square] = 0;
freq[time_square]++;
}
for (let [key, val] of Object.entries(freq))
{
if (val <= 0)
continue;
sum += (val * (val- 1)) / 2;
}
return sum;
}
let c = 5;
let arr = [];
let tmp = new Car(5, 12, 1);
arr.push(tmp);
tmp = new Car(16, 63, 5);
arr.push(tmp);
tmp = new Car(-10, 24, 2);
arr.push(tmp);
tmp = new Car(7, 24, 2);
arr.push(tmp);
tmp = new Car(-24, 7, 2);
arr.push(tmp);
console.log(solve(c, arr));
|
Share your thoughts in the comments
Please Login to comment...