Clustering Coefficient in Graph Theory
Last Updated :
31 Oct, 2022
In graph theory, a clustering coefficient is a measure of the degree to which nodes in a graph tend to cluster together. Evidence suggests that in most real-world networks, and in particular social networks, nodes tend to create tightly knit groups characterized by a relatively high density of ties; this likelihood tends to be greater than the average probability of a tie randomly established between two nodes (Holland and Leinhardt, 1971; Watts and Strogatz, 1998).
Two versions of this measure exist: the global and the local. The global version was designed to give an overall indication of the clustering in the network, whereas the local gives an indication of the embeddedness of single nodes.
Global clustering coefficient:
The global clustering coefficient is based on triplets of nodes. A triplet consists of three connected nodes. A triangle therefore includes three closed triplets, one centered on each of the nodes (n.b. this means the three triplets in a triangle come from overlapping selections of nodes). The global clustering coefficient is the number of closed triplets (or 3 x triangles) over the total number of triplets (both open and closed). The first attempt to measure it was made by Luce and Perry (1949). This measure gives an indication of the clustering in the whole network (global), and can be applied to both undirected and directed networks.
Local clustering coefficient:
A graph 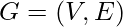 formally consists of a set of vertices V and a set of edges E between them. An edge
formally consists of a set of vertices V and a set of edges E between them. An edge 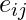 connects vertex
connects vertex 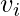 with vertex
with vertex 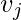 . The neighborhood
. The neighborhood 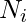 for a vertex
for a vertex 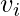 is defined as its immediately connected neighbors as follows:
is defined as its immediately connected neighbors as follows: 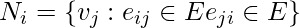 .
.
We define 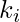 as the number of vertices,
as the number of vertices, 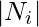 , in the neighborhood,
, in the neighborhood, 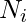 , of a vertex. The local clustering coefficient
, of a vertex. The local clustering coefficient 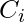 for a vertex
for a vertex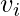 is then given by the proportion of links between the vertices within its neighborhood divided by the number of links that could possibly exist between them. For a directed graph,
is then given by the proportion of links between the vertices within its neighborhood divided by the number of links that could possibly exist between them. For a directed graph, 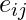 is distinct from
is distinct from 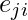 , and therefore for each neighborhood
, and therefore for each neighborhood 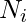 there are
there are 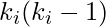 links that could exist among the vertices within the neighborhood (
links that could exist among the vertices within the neighborhood ( 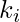 is the number of neighbors of a vertex). Thus, the local clustering coefficient for directed graphs is given as [2]
is the number of neighbors of a vertex). Thus, the local clustering coefficient for directed graphs is given as [2] 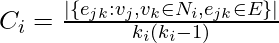 .
.
An undirected graph has the property that 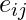 and
and 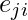 are considered identical. Therefore, if a vertex
are considered identical. Therefore, if a vertex 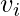 has
has 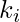 neighbors,
neighbors, 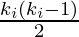 edges could exist among the vertices within the neighborhood. Thus, the local clustering coefficient for undirected graphs can be defined as
edges could exist among the vertices within the neighborhood. Thus, the local clustering coefficient for undirected graphs can be defined as 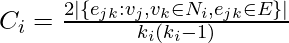 .
.
Let 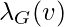 be the number of triangles on
be the number of triangles on 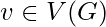 for undirected graph G. That is,
for undirected graph G. That is, 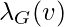 is the number of sub-graphs of G with 3 edges and 3 vertices, one of which is v. Let
is the number of sub-graphs of G with 3 edges and 3 vertices, one of which is v. Let 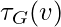 be the number of triples on
be the number of triples on 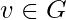 . That is,
. That is, 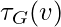 is the number of sub-graphs (not necessarily induced) with 2 edges and 3 vertices, one of which is v and such that v is incident to both edges. Then we can also define the clustering coefficient as lue
is the number of sub-graphs (not necessarily induced) with 2 edges and 3 vertices, one of which is v and such that v is incident to both edges. Then we can also define the clustering coefficient as lue 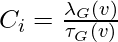 .
.
It is simple to show that the two preceding definitions are the same, since 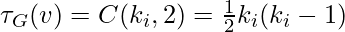 . These measures are 1 if every neighbor connected to
. These measures are 1 if every neighbor connected to 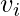 is also connected to every other vertex within the neighborhood, and 0 if no vertex that is connected to
is also connected to every other vertex within the neighborhood, and 0 if no vertex that is connected to 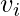 connects to any other vertex that is connected to
connects to any other vertex that is connected to 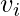 .
.
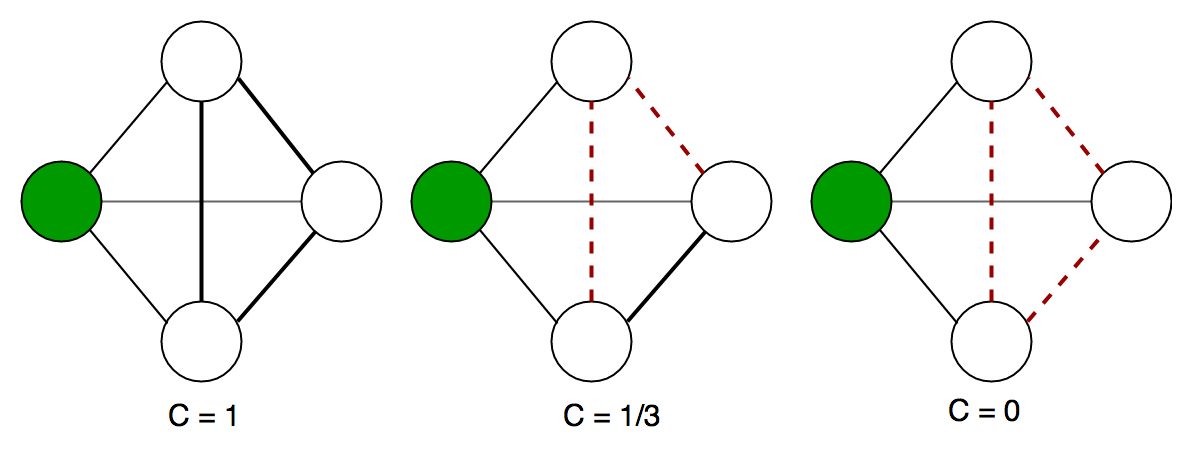
Example local clustering coefficient on an undirected graph. The local clustering coefficient of the green node is computed as the proportion of connections among its neighbours. Here is the code to implement the above clustering coefficient in a graph. It is a part of the networkx library and can be directly accessed using it.
Note: The above code is valid for undirected networks and not for the directed networks. The code below has been run on IDLE(Python IDE of windows). You would need to download the networkx library before you run this code. The part inside the curly braces represent the output. It is almost similar as Ipython(for Ubuntu users).
Python
>>> import networkx as nx
>>> G=nx.erdos_renyi_graph(10,0.4)
>>> cc=nx.average_clustering(G)
>>> cc
0.08333333333333333
>>> c=nx.clustering(G)
>>> c
{0: 0.0, 1: 0.3333333333333333, 2: 0.0, 3: 0.0, 4: 0.0, 5: 0.0, 6: 0.0,
7: 0.3333333333333333, 8: 0.0, 9: 0.16666666666666666}
|
The above two values give us the global clustering coefficient of a network as well as local clustering coefficient of a network. Next into this series, we will talk about another centrality measure for any given network.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...