Question 13. Find the value of k if x – 3 is a factor of k2x3 – kx2 + 3kx – k
Solution:
Let, f(x) = k2x3 – kx2 + 3kx – k
According to factor theorem
If x – 3 is the factor of f(x) then f(3) = 0
⇒ x – 3 = 0
⇒ x = 3
On substituting the value of x in f(x), we get
f(3) = k2(3)3 – k(3)2+ 3k(3) – k
= 27k2 – 9k + 9k – k
= 27k2 – k
= k( 27k – 1)
Equate f(3) to zero, to find k
⇒ f(3) = 0
⇒ k(27k – 1) = 0
⇒ k = 0 and 27k – 1 = 0
⇒ k = 0 and k = 1/27
When k = 0 and 1/27, (x – 3) will be the factor of f(x)
Question 14. Find the value of a and b, if x2 – 4 is a factor of f(x) = ax4 + 2x3 – 3x2 + bx – 4
Solution:
Given: f(x) = ax4 + 2x3 – 3x2 + bx – 4, g(x) = x2 – 4
We need to find the factors of g(x)
⇒ x2 – 4 = 0
⇒ x2 = 4
⇒ x = √4
⇒ x = ±2
(x – 2) and (x + 2) are the factors
According to factor theorem
If (x – 2) and (x + 2) are the factors of f(x)
the result of f(2) and f(-2) should be zero
Let, x – 2 = 0
⇒ x = 2
On substituting the value of x in f(x), we get
f(2) = a(2)4 + 2(2)3 – 3(2)2 + b(2) – 4
= 16a + 2(8) – 3(4) + 2b – 4
= 16a + 2b + 16 – 12 – 4
= 16a + 2b
Equate the value of f(2) to zero
⇒ 16a + 2b = 0
⇒ 2(8a + b) = 0
⇒ 8a + b = 0 -(1)
Let, x + 2 = 0
x = -2
On substituting the value of x in f(x), we get
f(-2) = a(-2)4 + 2(-2)3– 3(-2)2 + b(-2) – 4
= 16a + 2(-8) – 3(4) – 2b – 4
= 16a – 16 – 12 – 2b – 4
= 16a – 2b – 32
Equate the value of f(-2) to zero
⇒ 16a – 2b – 32 = 0
⇒ 16a – 2b – 32 = 0
⇒ 8a – b = 16 -(2)
On solving equation (1) and (2)
8a + b = 0
8a – b = 16
16a = 16
a = 1
On substituting the value of a in eq (1), we get
8(1) + b = 0
b = -8
The values are a = 1 and b = -8
Question 15. Find 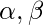 if (x + 1) and (x + 2) are factors of
if (x + 1) and (x + 2) are factors of 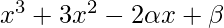
Solution:
Given: 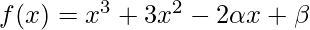 and factors are (x + 1) and (x + 2)
and factors are (x + 1) and (x + 2)
According to factor theorem,
If they are the factors of f(x) then results of f(-2) and f(-1) should be zero.
Let,
⇒ x + 1 = 0
⇒ x = -1
On substituting the value of x in f(x), we get
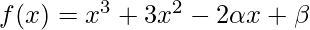
=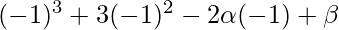
=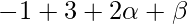
= 2\alpha +\beta +2 -(1)
Let,
⇒ x + 2 = 0
⇒ x = -2
On substituting the value of x in f(x), we get
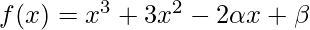
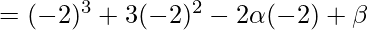
=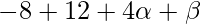
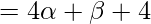 -(2)
-(2)
On solving eq(1) and (2)
⇒ 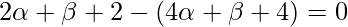
⇒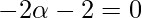
⇒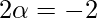
⇒ 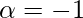
On substituting 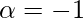 in equation(1)
in equation(1)
⇒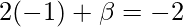
⇒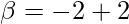
⇒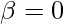
The values are 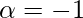 and
and 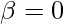
Question 16. Find the values of p and q so that x4 + px3 + 2x2 – 3x + q is divisible by x2 – 1
Solution:
Given: f(x) = x4 + px3 + 2x2 – 3x + q, g(x) = x2 – 1
First, we need to find the factors of x2 – 1
⇒ x2 – 1 = 0
⇒ x2 = 1
⇒ x = ±1
⇒ (x + 1) and (x – 1)
According to factor theorem
If x = 1, -1 are the factors of f(x) then f(1) = 0 and f(-1) = 0
Let, us take x + 1 = 0
x = -1
On substituting the value of x in f(x), we get
f(-1) = (-1)4 + p(-1)3 + 2(-1)2 – 3(-1) + q
= 1 – p + 2 + 3 + q
= -p + q + 6 -(1)
Let us take, x – 1 = 0
x = 1
On substituting the value of x in f(x), we get
f(1) = (1)4 + p(1)3 + 2(1)2 – 3(1) + q
= 1 + p + 2 – 3 + q
= p + q -(2)
On solving eq(1) and (2), we get
-p + q = -6
p + q = 0
2q = -6
q = -3
On substituting q value in eq(2), we get
p + q = 0
p – 3 = 0
p = 3
The value of p = 3 and q = -3
Question 17. Find the values of a and b so that (x + 1) and (x – 1) are the factors of x4 + ax3 – 3x2 + 2x + b
Solution:
Given: f(x) = x4 + ax3 – 3x2 + 2x + b
The factors are (x + 1) and (x – 1)
According to factor theorem
If x = 1, -1 are the factors of f(x) then f(1) = 0 and f(-1) = 0
Let, us take x + 1
⇒ x + 1 = 0
⇒ x = -1
On substituting the value of x in f(x), we get
f(-1) = (-1)4 + a(-1)3 – 3(-1)2 + 2(-1) + b
= 1 – a – 3 – 2 + b
= -a + b – 4 -(1)
Let, us take x – 1
⇒ x – 1 = 0
⇒ x = 1
On substituting the value of x in f(x), we get
f(1) = (1)4 + a(1)3 – 3(1)2 + 2(1) + b
= 1 + a – 3 + 2 + b
= a + b -(2)
On solving equation (1) and (2)
-a + b = 4
a + b = 0
2b = 4
b = 2
On substituting value of b in eq (2), we get
a + 2 = 0
a = -2
The values are a = -2 and b = 2
Question 18. If x3 + ax2 – bx + 10 is divisible by x3 – 3x + 2, find the values of a and b
Solution:
Given: f(x) = x3 + ax2 – bx + 10, g(x) = x3 – 3x + 2
First we need to find the factors of g(x)
g(x) = x3 – 3x + 2
=x3 – 2x – x + 2
= x(x – 2) – 1(x – 2)
= (x – 1)(x – 2) are the factors
Let us take (x – 1)
⇒ x – 1 = 0
⇒ x = 1
On substituting the value of x in f(x), we get
f(1) = 13 + a(1)2 – b(1) + 10
= 1 + a – b + 10
= a – b +11 -(1)
Let us take (x – 2)
⇒ x – 2 = 0
⇒ x = 2
On substituting the value of x in f(x), we get
f(2) = 23 + a(2)2 – b(2) + 10
= 8 + 4a – 2b + 10
= 4a – 2b + 18
Equating f(2) to zero
⇒ 4a – 2b +18 = 0
⇒ 2a – b + 9 = 0 -(2)
On solving eq(1) and (2), we get
a – b = -11
2a – b = -9
a = 2
On substituting the value of a in equation (1), we get
⇒ 2 – b = – 11
⇒ -b = -11 – 2
⇒ b = 13
The value is a = 2 and b = 13
Question 19. If both (x + 1) and (x – 1) are the factors of ax3 + x2 – 2x + b, Find the values of a and b
Solution:
Given: f(x) = ax3 + x2 – 2x + b, (x + 1) and (x – 1) are the factors
According to factor theorem,
If x = -1 & 1 are factors of f(x) then f(1) = 0 and f(-1) = 0
Let, x – 1 = 0
⇒ x = 1
On substituting the value of x in f(x), we get
f(1) = a(1)3 + (1)2 – 2(1) + b
= a +1 – 2 + b
= a + b – 1 -(1)
Let, x + 1 = 0
⇒ x = -1
On substituting the value of x in f(x), we get
f(-1) = a(-1)3 + (-1)2 – 2(-1) + b
= -a + 1 + 2 + b
= -a + b + 3 -(2)
On solving equation (1) and (2), we get
⇒ a + b = 1
⇒ -a + b = -3
⇒ 2b = -2
⇒ b = -1
On substituting the b in eq (1)
⇒ a – 1 = 1
⇒ a = 2
The values are a = 2 and b = -1
Question 20. What must be added to x3 – 3x2 – 12x + 19 so that the result is exactly divisible by x2 + x – 6
Solution:
Given: p(x) = x3 – 3x2 – 12x + 19, g(x) = x2 + x – 6
According to division algorithm when p(x) is divided by g(x),
the remainder will be the linear expression in x
Let, r(x) = ax + b is added to p(x)
⇒ f(x) = p(x) + r(x)
= f(x) = x3 – 3x2 – 12x + 19 + ax + b
We know that, g(x) = x2 + x – 6
First, we find the factors of g(x)
⇒ g(x) = x2 + x – 6
= x2 + 3x – 2x – 6
= x(x + 3) – 2(x + 3)
= (x – 2)(x + 3)
According to factor theorem
If (x – 2) & (x + 3) are factors of f(x) then f(-3) = 0 and f(2) = 0
Let, x + 3 = 0
⇒ x = -3
On substituting the value of x in f(x), we get
f(-3) = (-3)3 – 3(-3)2 – 12(-3) + 19 + a(-3) + b
= -27 – 27 – 3a + 24 + 19 + b
= -3a + b +1 -(1)
Let, x – 2 = 0
⇒ x = 2
On substituting the value of x in f(x), we get
f(2) = (2)3 – 3(2)2 – 12(2) + 19 + a(2) + b
= 8 – 12 + 2a – 24 + b
= 2a + b – 9 -(2)
On solving eq(1) and eq (2), we get
⇒ -3a + b = -1
⇒ 2a + b = 9
⇒ -5a = -10
⇒ a = 2
On substituting the value of a in eq(1)
⇒ -3(2) + b = -1
⇒ -6 + b = -1
⇒ b = 5
Therefore, r(x) = ax + b
= 2x + 5
Hence, x3 – 3x2 – 12x + 19 is divisible by x2 + x – 6 when it is added by 2x + 5.
Question 21. What must be added to x3 – 6x2 – 15x + 80 so that the result is exactly divisible by x2 + x – 12
Solution:
Let p(x) = x3 – 6x2 – 15x + 80, q(x) = x2 + x – 12
According to algorithm, when p(x) is divided by q(x) the remainder is a linear expression in x.
So, let r(x) = ax + b is subtracted from p(x), so that p(x) – q(x) is divisible by q(x)
Let, f(x) = p(x) – q(x)
q(x) = x2 + x – 12
= x2 + 4x – 3x – 12
= x(x + 4) – 3(x + 4)
=(x – 3)(x + 4)
Clearly, (x – 3) and (x + 4) are factors of q(x)
So, f(x) is divisible by q(x) if (x – 3) and (x + 4) are factors of q(x)
According to factor theorem
f(-4) = 0 and f(3) = 0
⇒ f(3) = 33 – 6(3)2 – 3(a + 15) + 80 – b = 0
= 27 – 54 – 3a – 45 + 80 – b
= -3a – b + 8 -(1)
Similarly,
f(-4) = 0
f(-4) = (-4)3 – 6(-4)2 – 4(a + 15) + 80 – b
⇒ -64 – 96 – 4a + 60 + 80 – b = 0
⇒ 4a – b – 20 = 0
On subtracting eq (1) and eq (2), we get
4a – b – 20 = 0 -(2)
⇒ 7a – 28 = 0
⇒ a = 28/7
⇒ a = 4
On Putting a = 4 in eq (1), we get
⇒ -3(4) – b = -8
⇒ -b – 12 = -8
⇒ -b = -8 + 12
⇒ b = -4
On substituting a and b values in r(x)
⇒ r(x) = ax + b
⇒ 4x – 4
Hence, p(x) is divisible by q(x), if r(x) = 4x – 4 is subtracted from it.
Question 22. What must be added to 3x3 + x2 – 22x + 9 so that the result is exactly divisible by 3x2 + 7x – 6
Solution:
Let, p(x) = 3x3+ x2– 22x + 9 and q(x) = 3x2 + 7x – 6
According to divisible theorem, when p(x) is divided by q(x), the reminder is linear equation in x.
Let, r(x) = ax + b is added to p(x), so that p(x) + r(x) is divisible by q(x)
f(x) = p(x) + r(x)
⇒ f(x) = 3x3 + x2 – 22x + 9(ax + b)
= 3x3 + x2+ x(a – 22) + b + 9
We know that,
q(x) = 3x2 + 7x – 6
= 3x2 + 9x – 2x – 6
= 3x(x + 3) – 2(x + 3)
= (3x – 2)(x + 3)
So, f(x) is divisible by q(x) if (3x – 2) and (x + 3) are the factors of f(x)
From factor theorem
f(2/3) = 0 and f(-3) = 0
Let, 3x – 2 = 0
3x = 2
x = 2/3
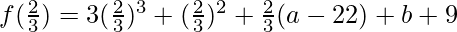
= 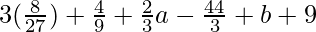
= 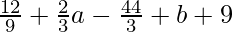
= 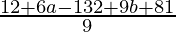
Equate to zero
⇒ 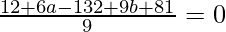
⇒ 6a + 9b – 39 = 0
⇒ 2a + 3b – 13 = 0 -(1)
Similarly,
Let, x + 3 = 0
⇒ x = -3
f(-3) = 3(-3)3 + (-3)2 – 3(a – 22) + b + 9
= -81 + 9 – 3a + 66 + b + 9
= -3a + b + 3
Equate to zero
⇒ -3a + b + 3 = 0
Multiply the given equation by 3
⇒ -9a + 3b + 9 = 0 -(2)
On Subtracting eq (1) from eq(2)
⇒ -9a + 3b + 9 – 2a – 3b + 13 = 0
⇒-11a + 22 = 0
⇒-11a = -22
⇒ a = 2
On substituting value of a in eq (1)
⇒ -3(2) + b = -3
⇒ -6 + b = -3
⇒ b = 3
Put the values in r(x)
r(x) = ax + b
= 2x + 3
Hence, p(x) is divisible by q(x), if r(x) = 2x + 3 is added to it.
Question 23. If x – 2 is a factor of each of the following two polynomials, find the value of a in each case:
(i) x3 – 2ax2 + ax – 1
(ii) x5 – 3x4 – ax3 + 3ax2 + 2ax + 4
Solution:
(i) Let f(x) = x3 – 2ax2 + ax – 1
According to factor theorem
If (x-2) is a factor of f(x) then f(2) = 0
Let, x – 2 = 0
⇒ x = 2
On substituting the value of x in f(x), we get
f(2) = 23 – 2a(2)2 + a(2) – 1
= 8 – 8a + 2a – 1
= -6a + 7
Equate f(2) to zero
⇒ -6a + 7 = 0
⇒ -6a = -7
⇒ a = 7/6
So, (x – 2) is the factor of f(x)
(ii) Let f(x) = x5 – 3x4 – ax3 + 3ax2 + 2ax + 4
According to factor theorem
If (x – 2) is a factor of f(x) then f(2) = 0
Let, x – 2 = 0
⇒ x = 2
On substituting the value of x in f(x), we get
f(2) = 25 – 3(2)4 – a(2)3 + 3a(2)2 + 2a(2) + 4
= 32 – 48 – 8a + 12 + 4a + 4
= 8a -12
Equate f(2) to zero
⇒ 8a – 12 = 0
⇒ a = 12/8
⇒ a = 3/2
So, (x – 2) is a factor of f(x)
Question 24. In each of the following two polynomials, find the value of a, if (x – a) is a factor:
(i) x6 – ax5 + x4 – ax3 + 3x – a + 2
(ii) x5 – a2x3 + 2x + a + 1
Solution:
(i) Let, f(x) = x6 – ax5 + x4 – ax3 + 3x – a + 2
Here, x – a = 0
⇒ x = a
On substituting the value of x in f(x), we get
f(a) = a6 – a(a)5 + (a)4 – a(a)3 + 3(a) – a + 2
= a6 – a6 + a4 – a4 + 3a – a + 2
= 2a+2
Equate to zero
⇒ 2a + 2 = 0
⇒ 2(a + 1) = 0
⇒ a = -1
So, (x – a) is a factor of f(x)
(ii) Let, f(x) = x5 – a2x3 + 2x + a + 1
Here, x – a = 0
⇒ x = a
On substituting the value of x in f(x), we get
f(a) = a5 – a2(a)3 + 2(a) + a + 1
= a5 – a5 + 2a + a + 1
= 3a + 1
Equate to zero
⇒ 3a + 1 = 0
⇒ 3a = -1
⇒ a = -1/3
So, (x – a) is a factor of f(x)
Question 25. In each of the following two polynomials, find the value of a, if (x + a) is a factor:
(i) x3 + ax2 – 2x + a +4
(ii) x4 – a2x2 + 3x – a
Solution:
(i) Let, f(x) = x3 + ax2 – 2x + a + 4
Here, x + a = 0
⇒ x = – a
On substituting the value of x in f(x), we get
f(-a) = (-a)3+ a(-a)2– 2(-a) + a + 4
= 3a + 4
Equate to zero
⇒ 3a + 4 = 0
⇒ 3a = -4
⇒ a = -4/3
So, (x + a) is a factor of f(x)
(ii) Let, f(x) = x4– a2x2 + 3x – a
Here, x + a = 0
⇒ x = -a
On substituting the value of x in f(x), we get
f(-a) = (-a)4 – a2(-a)2 + 3(-a) – a
= a4 – a4 – 3a – a
= -4a
Equate to zero
⇒ -4a = 0
⇒ a = 0
So, (x + a) is a factor of f(x)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...