Class 9 RD Sharma Solutions – Chapter 6 Factorisation of Polynomials- Exercise 6.4 | Set 1
Last Updated :
11 Feb, 2021
In each of the following, use factor theorem to find whether polynomial g(x) is a factor of polynomial f(x), or not(Question 1-7):
Question 1. f(x) = x3 – 6x2 + 11x – 6, g(x) = x – 3
Solution:
Given: f(x) = x3 – 6x2 + 11x – 6, g(x) = x – 3
Here,
x – 3 = 0
x = 3
To prove: g(x) is a factor of f(x), that is f(3) = 0
On substituting the value of x in f(x), we get
f(3) = 33 – 6 × 32 + 11 × 3 – 6
= 27 – (6 × 9) + 33 – 6
= 27 – 54 + 33 – 6
= 60 – 60
= 0
Since, the result is 0,
Hence, proved that g(x) is a factor of f(x).
Question 2. f(x) = 3x4 + 17x3 + 9x2 – 7x – 10, g(x) = x + 5
Solution:
Given: f(x) = 3x4 + 17x3 + 9x2 – 7x – 10, g(x) = x + 5
Here,
x + 5 = 0
x = -5
To prove: g(x) is a factor of f(x), that is f(-5) = 0
On substituting the value of x in f(x), we get
f(-5) = 3(-5)4+ 17(-5)3+ 9(-5)2– 7(-5) – 10
= 3 × 625 + 17 × (-125) + 9 × 25 + 35 – 10
= 1875 – 2125 + 225 + 35 – 10
= 2135 – 2135
= 0
Since, the result is 0,
Hence, proved that g(x) is a factor of f(x).
Question 3. f(x) = x5 + 3x4 – x3 – 3x2 + 5x + 15, g(x) = x + 3
Solution:
Given: f(x) = x5 + 3x4 – x3 – 3x2 + 5x + 15, g(x) = x + 3
Here,
x + 3 = 0
x = -3
To prove: g(x) is a factor of f(x), that is f(-3) = 0
On substituting the value of x in f(x), we get
f(-3) = (-3)5 + 3(-3)4 – (-3)3 – 3(-3)2 + 5(-3) + 15
= -243 + 243 + 27 – 27 – 15 + 15
= 0
Since, the result is 0,
Hence, proved that g(x) is a factor of f(x).
Question 4. f(x) = x3 – 6x2 – 19x + 84, g(x) = x – 7
Solution:
Given: f(x) = x3 – 6x2 – 19x + 84, g(x) = x – 7
Here,
x – 7 = 0
x = 7
To prove: g(x) is a factor of f(x), that is f(7) = 0
On substituting the value of x in f(x), we get
f(7) = 73 – 6 × 72 – 19 × 7 + 84
= 343 – (6 × 49) – (19 × 7) + 84
= 343 – 294 – 133 + 84
= 427 – 427
= 0
Since, the result is 0,
Hence, proved that g(x) is a factor of f(x).
Question 5. f(x) = 3x3 + x2 – 20x + 12, g(x) = 3x – 2
Solution:
Given: f(x) = 3x3 + x2 – 20x + 12, g(x) = 3x – 2
Here,
3x – 2 = 0
x = 2/3
To prove: g(x) is a factor of f(x), that is f(2/3) = 0
On substituting the value of x in f(x), we get
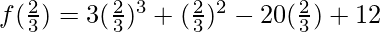
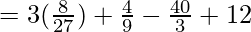
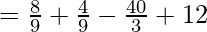

Taking L.C.M
= 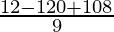
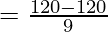
= 0
Since, the result is 0,
Hence, proved that g(x) is a factor of f(x).
Question 6. f(x) = 2x3 – 9x2 + x + 13, g(x) = 3 – 2x
Solution:
Given: f(x) = 2x3 – 9x2 + x + 13, g(x) = 3 – 2x
Here,
3 – 2x = 0
x = 3/2
To prove: g(x) is a factor of f(x), that is f(3/2) = 0
On substituting the value of x in f(x), we get

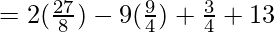
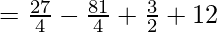
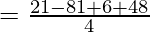
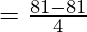
= 0
Since, the result is 0,
Hence, proved that g(x) is a factor of f(x).
Question 7. f(x) = x3 – 6x2 + 11x – 6, g(x) = x2 – 3x + 2
Solution:
Given: f(x) = x3 – 6x2 + 11x – 6, g(x) = x2 – 3x + 2
Here,
x2 – 3x + 2 = 0
On factorizing the above, we get
⇒ x2 – 3x + 2 = 0
⇒ x2 – 2x – x + 2 = 0
⇒ x(x – 2) – 1(x – 2)
⇒ (x – 1)(x – 2) are the factors
To prove: g(x) is a factor of f(x), that is f(1) and f(2) should be 0
Let x = 1
On substituting the value of x in f(x), we get
f(1) = 13 – 6 × 12 + 11 × 1 – 6
= 1 – 6 + 11 – 6
= 12 – 12
= 0
Let x = 2
On substituting the value of x in f(x), we get
f(x) = 23 – 6 × 22 + 11 × 2 – 6
= 8 – (6 × 4) + 22 – 6
= 8 – 24 +22 – 6
= 30 – 30
= 0
Since, the results are 0 g(x) is the factor of f(x)
Question 8. Show that (x – 2), (x + 3) and (x – 4) are the factors of x3 – 3x2 – 10x + 24
Solution:
Given:
f(x) = x3 – 3x2 – 10x + 24
Factors given are (x – 2), (x + 3) and (x – 4)
To prove: g(x) is a factor of f(x), that is f(2), f(-3), f(4) should be 0
Here, x – 2 = 0
Let, x = 2
On substituting the value of x in f(x), we get
f(2) = 23 – 3 × 22 – 10 × 2 + 24
= 8 – (3 × 4) – 20 + 24
= 8 – 12 – 20 + 24
= 32 – 32
= 0
Here, x + 3 = 0
Let, x = -3
On substituting the value of x in f(x), we get
f(-3) = (-3)3 – 3 × (-3)2 – 10 × (-3) + 24
= -27 -3(9) + 30 + 24
= -27- 27 + 30 + 24
= 54 – 54
= 0
Here, x – 4 = 0
Let, x = 4
On substituting the value of x in f(x), we get
f(4) = (4)3 – 3 × (4)2 – 10 × (4) + 24
= 64 – 3(16) – 40 + 24
= 64 – 48 – 40 + 24
= 84 – 84
= 0
Since, the results are 0, g(x) is the factor of f(x)
Question 9. Show that (x + 4), (x – 3) and (x – 7) are the factors of x3 – 6x2 – 19x + 84
Solution:
Given:
f(x) = x3 – 6x2– 19x + 84
Factors given are (x + 4), (x – 3) and (x – 7)
To prove: g(x) is a factor of f(x), that is f(4), f(3), f(-7) should be 0
Here, x + 4 = 0
Let, x = -4
On substituting the value of x in f(x), we get
f(-4) = (-4)3 – 6(-4)2 – 19(-4) + 84
= -64 – (6 × 16) – 19 × (-4) + 84
= -64 – 96 + 76 + 84
= 160 – 160
= 0
Here, x – 3 = 0
Let, x = 3
On substituting the value of x in f(x), we get
f(3) = (3)3 – 6(3)2 – 19(3) + 84
= 27 – 6(9) – 19 × 3 + 84
= 27 – 54 – 57 + 84
= 111 – 111
= 0
Here, x – 7 = 0
Let, x = 7
On substituting the value of x in f(x), we get
f(7) = (7)3 – 6(7)2 – 19(7) + 84
= 343 – 6(49) – 19 × 7 + 84
= 343 – 294 – 133 + 84
= 427 – 427
= 0
Since, the results are 0, g(x) is the factor of f(x)
Question 10. For what value of a is (x – 5) a factor of x3 – 3x2 + ax – 10
Solution:
Here, f(x) = x3 – 3x2 + ax – 10
By factor theorem
If (x – 5) is the factor of f(x) then, f(5) = 0
⇒ x – 5 = 0
⇒ x = 5
On substituting the value of x in f(x), we get
f(5) = 53 – 3 × 52 + a × 5 – 10
= 125 – (3 × 25) + 5a -10
= 125 – 75 + 5a – 10
= 5a + 40
Equate f(5) to zero
f(5) = 0
⇒ 5a + 40 = 0
⇒ 5a = -40
⇒ a = -40/5
⇒ a = -8
When a = -8, then (x – 5) will be factor of f(x)
Question 11. Find the value of such that (x – 4) is a factor of 5x3 – 7x2 – ax – 28
Solution:
Given: f(x) = 5x3– 7x2– ax – 28
Using factor theorem
(x – 4) is the factor of f(x), then f(4) = 0
⇒ x – 4 = 0
⇒ x = 4
On substituting the value of x in f(x), we get
f(4) = 5(4)3 – 7(4)2 – a × 4 – 28
= 5(64) – 7(16) – 4a – 28
= 320 – 112 – 4a – 28
= 180 – 4a
Equate f(4) to zero, to find a
f(4) = 0
⇒ 180 – 4a = 0
⇒ a = 180/4
⇒ a = 45
When a = 45, then (x – 4) will be factor of f(x)
Question 12. Find the value of a, if (x + 2) is a factor of 4x4 + 2x3 – 3x2 + 8x + 5a
Solution:
Given: f(x) = 4x4+ 2x3– 3x2+ 8x + 5a
Using factor theorem
If (x + 2) is the factor of f(x), then f(-2) should be zero
⇒ x + 2 =0
⇒ x = -2
On substituting the value of x in f(x), we get
f(-2) = 4(-2)4+ 2(-2)3– 3(-2)2+ 8(-2) + 5a
= 4(16) + 2 (-8) – 3(4) – 16 + 5a
= 64 – 16 – 12 -16 + 5a
= 5a + 20
Equate f(-2) to 0
f(-2) = 4(-2)2+ 2(-2)3– 3(-2)2+ 8(-2) + 5a
= 4(16) + 2(-8) – 3(4) – 16 + 5a
= 64 – 16 – 12 – 16 + 5a
= 5a + 20
Equate f(-2) to 0
f(-2) = 0
⇒ 5a + 20 = 0
⇒ 5a = – 20
⇒ a = -4
When a = -4, then (x + 2) is the factor of f(x)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...