Class 9 RD Sharma Solutions – Chapter 2 Exponents of Real Numbers- Exercise 2.2 | Set 2
Last Updated :
30 Apr, 2021
Question 12. Determine (8x)x, if 9x+2 = 240 + 9x.
Solution:
We have,
=> 9x+2 = 240 + 9x
=> 9x+2 − 9x = 240
=> 9x (92 − 1) = 240
=> 9x = 240/80
=> 32x = 3
=> 2x = 1
=> x = 1/2
Therefore, (8x)x = [8 × (1/2)]1/2
= 41/2
= 2
Question 13. If 3x+1 = 9x−2, find the value of 21+x.
Solution:
We have,
=> 3x+1 = 9x−2
=> 3x+1 = (32)x−2
=> 3x+1 = 32x−4
=> x + 1 = 2x − 4
=> x = 5
Therefore, 21+x = 21+5
= 26
= 64
Question 14. If 34x = (81)−1 and (10)1/y = 0.0001, find the value of 2−x+4y.
Solution:
We are given,
=> 34x = (81)−1
=> 34x = (34)−1
=> 34x = (3)−4
=> 4x = −4
=> x = −1
And also, (10)1/y = 0.0001
=> (10)1/y = (10)−4
=> 1/y = −4
=> y = −1/4
Therefore, 2−x+4y = 21+4(−1/4)
= 21−1
= 1
Question 15. If 53x = 125 and 10y = 0.001. Find x and y.
Solution:
We are given,
=> 53x = 125
=> 53x = 53
=> 3x = 3
=> x =1
Also, (10)y = 0.001
=> 10y = 10−3
=> y = −3
Therefore, the value of x is 1 and the value of y is –3.
Question 16. Solve the following equations:
(i) 3x+1 = 27 × 34
Solution:
We have,
=> 3x+1 = 27 × 34
=> 3x+1 = 33 × 34
=> 3x+1 = 37
=> x + 1 = 7
=> x = 6
(ii) ![Rendered by QuickLaTeX.com 4^{2x}=\left(\sqrt[3]{16}\right)^{\frac{-6}{y}}=(\sqrt{8})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e4db93522d462459f93ca4538e51de9b_l3.png)
Solution:
We have,
=> ![Rendered by QuickLaTeX.com 4^{2x}=\left(\sqrt[3]{16}\right)^{\frac{-6}{y}}=(\sqrt{8})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43c5be86e71e25ca031befcf436bfe68_l3.png)
=> ![Rendered by QuickLaTeX.com (2^2)^{2x}=\left(\sqrt[3]{2^4}\right)^{\frac{-6}{y}}=(\sqrt{2^3})^2](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2cab1ad8c40b06925ea7a539c7f8024c_l3.png)
=> 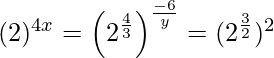
=> 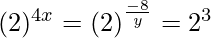
=> 4x = −8/y = 3
=> x = 3/4 and y = −8/3
(iii) 3x−1 × 52y−3 = 225
Solution:
We have,
=> 3x−1 × 52y−3 = 225
=> 3x−1 × 52y−3 = 32 × 52
=> x − 1 = 2 and 2y − 3 = 2
=> x = 3 and 2y = 5
=> x = 3 and y = 5/2
(iv) 8x+1 = 16y+2 and (1/2)3+x = (1/4)3y
Solution:
We have,
=> 8x+1 = 16y+2
=> (23)x+1 = (24)y+2
=> 23x+3 = 24y+8
=> 3x + 3 = 4y + 8 . . . . (1)
Also, (1/2)3+x = (1/4)3y
=> (1/2)3+x = [(1/2)2]3y
=> (1/2)3+x = (1/2)6y
=> 3 + x = 6y
=> x = 6y − 3 . . . . (2)
Putting (2) in (1), we get,
=> 3(6y − 3) + 3 = 4y + 8
=> 18y − 9 + 3 = 4y + 8
=> 14y = 14
=> y = 1
Putting y = 1 in (2), we get,
x = 6(1) − 3 = 6 − 3 = 3
Therefore, the value of x is 1 and the value of y is –3.
(v) 4x−1 × (0.5)3−2x = (1/8)x
Solution:
We have,
=> 4x−1 × (0.5)3−2x = (1/8)x
=> (22)x−1 × (1/2)3−2x = [(1/2)3]x
=> 22x−2 × 22x−3 = 2−3x
=> 22x−2+2x−3 = 2−3x
=> 24x−5 = 2−3x
=> 4x − 5 = −3x
=> 7x = 5
=> x = 5/7
(vi) 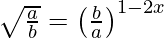
Solution:
We have,
=> 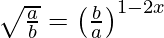
=> 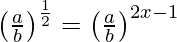
=> 1/2 = 2x − 1
=> 2x = 3/2
=> x = 3/4
Question: 17. If a and b are distinct positive primes such that, ![Rendered by QuickLaTeX.com \sqrt[3]{a^6b^{-4}}=a^xb^{2y}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbe7ef4d0a788a4bf5d750098215cd64_l3.png) find x and y.
find x and y.
Solution:
We have,
=> ![Rendered by QuickLaTeX.com \sqrt[3]{a^6b^{-4}}=a^xb^{2y}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cbe7ef4d0a788a4bf5d750098215cd64_l3.png)
=> (a6 b−4)1/3 = axb2y
=> a6/3 b−4/3 = axb2y
=> a2 b−4/3 = axb2y
=> x = 2 and 2y = −4/3
=> x = 2 and y = −2/3
Question 18. If a and b are different positive primes such that,
(i) 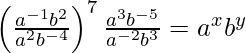 , find x and y.
, find x and y.
Solution:
We have,
=> 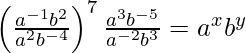
=> (a−1−2 b2+4)7 ÷ (a3+2 b−5−3) = axby
=> (a−3 b6)7 ÷ (a5 b−8) = axby
=> (a−21 b42) ÷ (a5 b−8) = axby
=> (a−21−5 b42+8) = axby
=> (a−26 b50) = axby
=> x = −26, y = 50
(ii) (a + b)−1(a−1 + b−1) = axby, find x+y+2.
Solution:
We have,
=> (a + b)−1(a−1 + b−1) = axby
=> 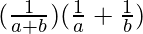 = axby
= axby
=>  = axby
= axby
=> 1/ab = axby
=> a−1b−1 = axby
=> x = −1 and y = −1
So, x+y+2 = −1−1+2 = 0.
Question 19. If 2x × 3y × 5z = 2160, find x, y and z. Hence compute the value of 3x × 2−y × 5−z.
Solution:
We are given,
=> 2x × 3y × 5z = 2160
=> 2x × 3y × 5z = 24 × 33 × 51
=> x = 4, y = 3, z = 1
Therefore, 3x × 2−y × 5−z = 34 × 2−3 × 5−1
= (81) (1/8) (1/5)
= 81/40
Question 20. If 1176 = 2a × 3b × 7c, find the values of a, b and c. Hence, compute the value of 2a × 3b × 7-c as a fraction.
Solution:
We are given,
=> 1176 = 2a × 3b × 7c
=> 23 × 31 × 72 = 2a × 3b × 7c
=> a = 3, b = 1, c = 2
Therefore, 2a × 3b × 7−c = 23 × 31 × 7−2
= (8) (3) (1/49)
= 24/49
Question 21. Simplify
(i) 
Solution:
We have,
= 
= (xa+b−c)a−b (xb+c−a)b−c (xc+a−b)c−a
= 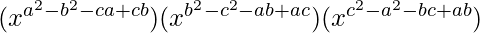
= 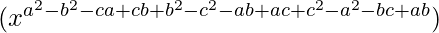
= x0
= 1
(ii) ![Rendered by QuickLaTeX.com \sqrt[lm]{\frac{x^l}{x^m}}×\sqrt[mn]{\frac{x^m}{x^n}}×\sqrt[nl]{\frac{x^n}{x^l}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5999c7417ca8e24471478ce989cfe1a3_l3.png)
Solution:
We have,
=> ![Rendered by QuickLaTeX.com \sqrt[lm]{\frac{x^l}{x^m}}×\sqrt[mn]{\frac{x^m}{x^n}}×\sqrt[nl]{\frac{x^n}{x^l}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9d33ca8f7d224eec85584481f585c8c8_l3.png)
=> 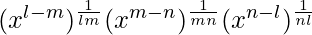
=> 
=> 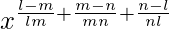
=> 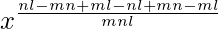
=> 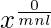
=> x0
= 1
Question 22. Show that 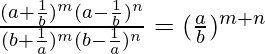 .
.
Solution:
We have,
L.H.S. = 
= 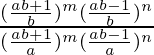
= 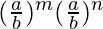
= 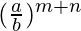
= R.H.S.
Hence proved.
Question 23. (i) If a = xm+nyl, b = xn+lym and c = xl+myn, prove that am−n bn−l cl−m = 1.
Solution:
Given, a = xm+nyl, b = xn+lym and c = xl+myn.
We have,
L.H.S. = am−n bn−l cl−m
= (xm+nyl)m−n(xn+lym)n−l(xl+myn)l−m
= 
= 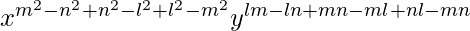
= x0y0
= 1
= R.H.S.
Hence proved.
(ii) If x = am+n, y = an+l and z = al+m, prove that xmynzl = xnylzm.
Solution:
Given, x = am+n, y = an+l and z = al+m.
We have,
L.H.S. = xmynzl
= (am+n)m (an+l)n (al+m)l
= 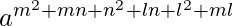
= 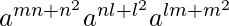
= (am+n)n (an+l)l (al+m)m
= xnylzm
= R.H.S.
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...