Class 9 RD Sharma Solutions – Chapter 14 Quadrilaterals – Exercise 14.2
Last Updated :
28 Mar, 2021
Question 1. Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°. Find the measure of each angle of the parallelogram.
Solution:
Given: Two opposite angles of a parallelogram are (3x – 2)° and (50 – x)°.
(3x – 2)°= (50 – x)° [Opposite sides of a parallelogram are equal]
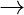 3x + x = 50 + 2
3x + x = 50 + 2
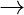 4x = 52
4x = 52
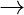 x = 13
x = 13
Angle x is 13°
 (3x – 2) = (3*13 – 2) = 37°
(3x – 2) = (3*13 – 2) = 37°
(50 – x)° = (50 – 13)°= 37°
 x + 37°= 180° [Adjacent angles of a parallelogram are supplementary]
x + 37°= 180° [Adjacent angles of a parallelogram are supplementary]
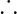 x = 180°− 37°= 143°
x = 180°− 37°= 143°
Hence, required angles are : 37°, 143°, 37°, 143°.
Question 2. If an angle of a parallelogram is two-third of its adjacent angle, find the angles of the parallelogram.
Solution:
Let the measure of the angle be x.
Therefore, the measure of the angle adjacent is 2x/3
Hence, x + 2x/3 = 180° [Consecutive angles of a parallelogram are supplementary]
2x + 3x = 540°
 5x = 540°
5x = 540°
 x = 108°
x = 108°
Now,
⟹ x + 108°= 180° [Consecutive angles of a parallelogram are supplementary]
⟹ x + 108°= 180°
⟹ x = 180°- 108°= 72°
⟹ x = 72°
 required angles are180°, 72°, 180°, 72°
required angles are180°, 72°, 180°, 72°
Question 3. Find the measure of all the angles of a parallelogram, if one angle is 24°less than twice the smallest angle.
Solution:
x + 2x – 24°= 180° [Consecutive angles of a parallelogram are supplementary]
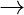 3x – 24°= 180°
3x – 24°= 180°
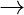 3x = 108° + 24°
3x = 108° + 24°
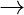 3x = 204°
3x = 204°
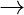 x = 204/3 = 68°
x = 204/3 = 68°
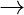 x = 68°
x = 68°
Other angle of parallelogram=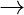 2x – 24°= 2*68°- 24°= 112°
2x – 24°= 2*68°- 24°= 112°
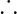 required angles are 68°,112°,68°,112°
required angles are 68°,112°,68°,112°
Question 4. The perimeter of a parallelogram is 22 cm. If the longer side measures 6.5 cm what is the measure of the shorter side?
Solution:
Given: perimeter of a parallelogram is 22 cm
Let us consider the shorter side be ‘y’.
 perimeter = y + 6.5 + 6.5 + x [Sum of all sides]
perimeter = y + 6.5 + 6.5 + x [Sum of all sides]
22 = 2(y + 6.5)
11 = y + 6.5
 y = 11 – 6.5 = 4.5 cm
y = 11 – 6.5 = 4.5 cm
Hence, the measure of the shorter side = 4.5 cm
Question 5. In a parallelogram ABCD, ∠D = 135°. Determine the measures of ∠A and ∠B.
Solution:
In a parallelogram ABCD
Given: ∠D=135°
So, ∠D + ∠C = 180° [Consecutive angles of a parallelogram are supplementary]
∠C = 180°− 135°
∠C = 45°
In a parallelogram opposite sides are equal.
∠A = ∠C = 45° [opposite sides of parallelogram are equal]
∠B = ∠D = 135°
hence, the measures of ∠A and ∠B are 45°,135°respectively.
Question 6. ABCD is a parallelogram in which ∠A = 70°. Compute ∠B, ∠C and ∠D.
Solution:
In a parallelogram ABCD
Given: ∠A = 70°
∠A + ∠B = 180° [Consecutive angles of a parallelogram are supplementary]
70°+ ∠B = 180° [given ∠A = 70°]
∠B = 180°− 70°
∠B = 110°
Now,
∠A = ∠C = 70° [opposite sides of parallelogram are equal]
∠B = ∠D = 110°
hence, the measures of ∠A and ∠B are 70°,110°respectively.
Question 7. In Figure, ABCD is a parallelogram in which ∠A = 60°. If the bisectors of ∠A, and ∠B meet at P, prove that AD = DP, PC = BC and DC = 2AD.
Solution:

Given: ∠A = 60°
To prove: AD = DP, PC = BC and DC = 2AD
AP bisects ∠A
so, ∠DAP = ∠PAB = 30°
Now,
∠A + ∠B = 180° [Consecutive angles of a parallelogram are supplementary]
∠B + 60°= 180°
∠B = 180°− 60°
∠B = 120°
BP bisects ∠B
so, ∠PBA = ∠PBC = 60°
∠PAB = ∠APD = 30°[Alternate interior angles]
Therefore, AD = DP [Sides opposite to equal angles are in equal length]
Similarly
∠PBA = ∠BPC = 60° [Alternate interior angles]
Therefore, PC = BC
DC = DP + PC
DC = AD + BC [ DP = AD and PC = BC ]
DC = 2AD [Since, AD = BC, The opposite sides of parallelogram are parallel and congruent]
hence proved.
Question 8. In figure, ABCD is a parallelogram in which ∠DAB = 75°and ∠DBC = 60°. Compute ∠CDB, and ∠ADB.
Solution:

Given: ∠DAB = 75°and ∠DBC = 60°
To find ∠CDB and ∠ADB
∠CBD = ∠ADB = 60° [Alternate interior angle. AD∥ BC and BD is the transversal]
In BDA
BDA
∠DAB + ∠ADB + ∠ABD = 180° [Angle sum property]
 75°+ 60°+ ∠CDB = 180°
75°+ 60°+ ∠CDB = 180°
 ∠ABD = 180°− (135°)
∠ABD = 180°− (135°)
 ∠ABD = 45°
∠ABD = 45°
∠ABD = ∠CDB = 45° [Alternate interior angle. AD∥ BC and BD is the transversal]
Hence, ∠CDB = 45°, ∠ADB = 60°
Question 9. In figure, ABCD is a parallelogram and E is the mid-point of side BC. If DE and AB when produced meet at F, prove that AF = 2AB.
Solution:

Given: ABCD is a parallelogram and E is the mid-point of side BC.
To prove: AF = 2AB.
Now,
In ΔBEF and ΔCED
∠BEF = ∠CED [Verified opposite angle]
BE = CE [Since, E is the mid-point of BC]
∠EBF = ∠ECD [Since, Alternate interior angles are equal]
 ΔBEF ≅ ΔCED [ASA congruence]
ΔBEF ≅ ΔCED [ASA congruence]
 BF = CD [Corresponding Parts of Congruent Triangle]
BF = CD [Corresponding Parts of Congruent Triangle]
AF = AB + AF
AF = AB + CD [BF = CD by Corresponding Parts of Congruent Triangle ]
AF = AB + AB [CD=AB, The opposite sides of parallelogram are parallel and congruent]
AF = 2AB.
Hence proved.
Question 10. Which of the following statements are true (T) and which are false (F)?
(i) In a parallelogram, the diagonals are equal.
(ii) In a parallelogram, the diagonals bisect each other.
(iii) In a parallelogram, the diagonals intersect each other at right angles.
(iv) In any quadrilateral, if a pair of opposite sides is equal, it is a parallelogram.
(v) If all the angles of a quadrilateral are equal, it is a parallelogram.
(vi) If three sides of a quadrilateral are equal, it is a parallelogram.
(vii) If three angles of a quadrilateral are equal, it is a parallelogram.
(viii) If all the sides of a quadrilateral are equal, it is a parallelogram.
Solution:
(i) False
(ii) True
(iii) False
(iv) False
(v) True
(vi) False
(vii) False
(viii) True
Share your thoughts in the comments
Please Login to comment...