Class 9 RD Sharma Solutions – Chapter 12 Heron’s Formula- Exercise 12.1
Last Updated :
11 Feb, 2021
Question 1. Find the area of a triangle whose sides are respectively 150 cm, 120 cm and 200 cm.
Solution:
By Heron’s formula, we have,
Area of triangle = ![Rendered by QuickLaTeX.com \sqrt[]{s(s-a)(s-b)(s-c)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0373db9d9b77b3baf417ec244970fa70_l3.png)
Semi-perimeter, s = (a + b + c)/2
where a, b and c are sides of triangle
We have,
a = 150 cm
b = 120 cm
c = 200 cm
Step 1: Computing s
s = (a+b+c)/2
s = (150+200+120)/2
s = 235 cm
Step 2: Computing area of a triangle
![Rendered by QuickLaTeX.com Area= \sqrt[]{235(235-120)(235-150)(235-200) } \\ =\sqrt[]{235(35)(115)(85) } \\=\sqrt[]{8093375}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-685ac4e2ed3daf7bd871857a38f99173_l3.png)
= 8966.56
Area of triangle is 8966.56 sq. cm.
Question 2. Find the area of a triangle whose sides are respectively 9 cm, 12 cm and 15 cm.
Solution:
By Heron’s formula, we have,
Area of triangle = \sqrt[]{s(s-a)(s-b)(s-c)}
Semi-perimeter, s = (a + b + c)/2
where a, b and c are sides of triangle
We have,
a = 9 cm
b = 12 cm
c = 15 cm
Step 1: Computing s
s = (a+b+c)/2
s = (9 + 12 + 15)/2
s = 18 cm
Step 2: Computing area of a triangle
![Rendered by QuickLaTeX.com Area= \sqrt[]{18(18-9)(18-12)(18-15) } \\ =\sqrt[]{18 * 9 * 6 * 3} \\=\sqrt[]{2916}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6e38c3192b11dc3c20f071b3d22f6cee_l3.png)
= 54
Area of triangle is 54 sq. cm.
Question 3. Find the area of a triangle two sides of which are 18 cm and 10 cm and the perimeter is 42 cm.
Solution:
We have,
a = 18 cm, b = 10 cm, and perimeter = 42 cm
Let us assume c to be the third side of the triangle.
Step 1: Computing third side of the triangle, that is c,
We know, perimeter = 2s,
2s = 42
s = 21
Also,
s = (a+b+c)/2
Substituting s, we get
21 = (18+10+c)/2
42 = 28 + c
c = 14 cm
Step 2: Computing area of triangle,
![Rendered by QuickLaTeX.com Area= \sqrt[]{21(21-18)(21-10)(21-14) } \\ =\sqrt[]{21 * 3 * 11 * 7} \\=21\sqrt[]{11}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-83c5bb1e77c8e8326e0ebaf6fcfd5992_l3.png)
Question 4. In a triangle ABC, AB = 15cm, BC = 13cm and AC = 14cm. Find the area of triangle ABC and hence its altitude on AC.
Solution:
By Heron’s formula, we have,
Area of triangle =\sqrt[]{s(s-a)(s-b)(s-c)}
Semi-perimeter, s = (a + b + c)/2
where a, b and c are sides of triangle
We have,
a = 150 cm
b = 120 cm
c = 200 cm
Step 1: Computing s
s = (a+b+c)/2
s = (15+13+14)/2
s = 21 cm
Step 2: Computing area of a triangle
![Rendered by QuickLaTeX.com Area= \sqrt[]{21(21-13)(21-14)(21-15) } \\ =\sqrt[]{21 * 8 * 7 * 6} \\=\sqrt[]{7056}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dbfd5bc0c79de1ae4d811c4e5c1ec1c8_l3.png)
= 84
Area = 84 cm2
Let us assume, BE is a perpendicular on AC
We know, area of triangle = ½ x Base x Height
=> ½ × BE × AC = 84
BE = 12cm
Therefore, the length of altitude is 12 cm.
Question 5. The perimeter of a triangular field is 540 m and its sides are in the ratio 25:17:12. Find the area of the triangle.
Solution:
Let the sides of a given triangle be a = 25x, b = 17x, c = 12x respectively,
We have, Perimeter of triangle = 540 cm
Also, Perimeter = 2s
2s = a + b + c
=> a + b + c = 540 cm
=> 25x + 17x + 12x = 540 cm
=> 54x = 540 cm
=> x = 10 cm
So, the sides of a triangle are
a = 250 cm
b = 170 cm
c = 120 cm
Also, semi perimeter, s = (a+b+c)/2
= 540/2
= 270
s = 270 cm
And,
![Rendered by QuickLaTeX.com Area= \sqrt[]{270(270-250)(270-170)(270-120) } \\ =\sqrt[]{270 * 20 * 100 * 150} \\=\sqrt[]{81000000}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c00c27a3dab2eb883a16bdd3bb89e4f9_l3.png)
= 9000
Hence, the area of the triangle is 9000 sq. cm.
Question 6. The perimeter of a triangular field is 300 m and its sides are in the ratio 3:5:7. Find the area of the triangle.
Solution:
Let the sides of a given triangle be a = 3x, b = 5x, c = 7x respectively,
We have, Perimeter of triangle = 300 m
Also, Perimeter = 2s
2s = a + b + c
=> a + b + c = 300 m
=> 3x + 5x + 7x = 300 m
=> 15x = 300 m
=> x = 20 cm
So, the sides of a triangle are
a = 60 m
b = 100 m
c = 140 m
Also, semi perimeter, s = (a+b+c)/2
= 300/2
= 150
s = 150 m
And,
![Rendered by QuickLaTeX.com Area= \sqrt[]{150(150-60)(150-100)(150-140) } \\ =\sqrt[]{150 * 90 * 50 * 10} \\=1500\sqrt[]{3}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0dd1087f9845b7e8cd7dbd8470fdcb1e_l3.png)
Hence, the area of the triangle is 1500\sqrt[]{3} sq. cm.
Question 7. The perimeter of triangular field is 240dm. If two of its sides are 78dm and 50 dm, find the length of the perpendicular of the side 50dm from the opposite vertex.
Solution:
Semi-perimeter, s = (a + b + c)/2
where a, b and c are sides of triangle
Perimeter = 2s
2s = 240dm
s = 120dm
Let the third side be x.
Now,
120 = (78 + 50 + x)/2
x = 112 dm
Computing area of triangle, we have,
![Rendered by QuickLaTeX.com Area= \sqrt[]{120(120-112)(120-50)(120-78) } \\ =\sqrt[]{(3 * 8 * 7 * 10)^2} \\=\sqrt[]{3 * 8 * 7 * 10} \\={3 * 8 * 7 * 10} sq. dm. \\={1680} sq. dm.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-018a575d172de241a8db91e7ef9e3733_l3.png)
Let us assume the length of altitude of length 50dm be a.
We know, area of triangle = ½ x Base x Height
=> ½ × a × 50 = 1680
BE = 67.2dm
Therefore, the length of altitude is 67.2 dm.
Question 8. A triangle has sides 35cm, 54 cm and 61cm. Find its area.Find the smallest altitude.
Solution:
Semi-perimeter, s = (a + b + c)/2
where a, b and c are sides of triangle
s = (34+54+61)/2
=75 cm
Computing area of triangle, we have,
![Rendered by QuickLaTeX.com Area= \sqrt[]{75(75-35)(75-54)(75-61) } \\ =\sqrt[]{(75 * 40 * 21 * 14)^2} \\=\sqrt[]{(5 * 3 * 7 * 2)^2 * 2 * 5} \\={5 * 3 * 7 * 2}\sqrt{10} sq. cm. \\={420}\sqrt{5} sq. cm.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b04244011ea50f26c0fd8353ec4dea19_l3.png)
Let us assume the length of altitude of length 50dm be a.
We know, area of triangle = ½ x Base x Height
For different measurements, the area remains constant.
The smallest altitude always lies on the longest side.
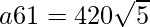
=> a = 30.79 cm
Therefore, the length of altitude = 30.79 cm
Question 9. The perimeter of a triangular field is 144 cm and its sides are in the ratio 3:4:5. Find the area of the triangle and height corresponding to the longest side.
Solution:
Let the sides of a given triangle be a = 3x, b = 4x, c = 5x respectively,
We have, Perimeter of triangle = 144 cm
Also, Perimeter = 2s
2s = a + b + c
=> a + b + c = 144 cm
=> 3x + 4x + 5x = 144 cm
=> 12x = 144cm
=> x = 12 cm
So, the sides of a triangle are
a = 36 cm
b = 48 m
c = 60 m
Also, semi perimeter, s = (a+b+c)/2
= 144/2
= 72
s = 72 cm
And,
![Rendered by QuickLaTeX.com Area= \sqrt[]{72(72-60)(72-48)(72-36) } \\ =\sqrt[]{72 * 12 * 24 * 36}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3679a79ccc368a5ba4657c2e8feca024_l3.png) \\=1500\sqrt[]{3}
\\=1500\sqrt[]{3}
a = 9.6 cm
Question 10. The perimeter of the isosceles triangle is 42cm, and its base (3/2) timeseach of its equal sides. Find length of each sides.
Solution:
Let the equal sides be a.
So, base = 3/2a
Perimeter of triangle = 3/2a + a + a
7a/2 = 42 cm
a = 12 cm
Therefore, sides of the triangle are, 12 cm is each of the equal sides
and 3/2a = 18 cm = base
Semi perimeter = 42/2 cm = 21 cm
By heron’s formula,
![Rendered by QuickLaTeX.com Area= \sqrt[]{21(21-12)(21-18)(21-12) } \\ =\sqrt[]{21 * 3 * 9 * 9} \\=\sqrt[]{7 * 3 * 3 * 9 * 9} \\={27}\sqrt{7} sq. cm. \\=71.43 sq. cm.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-595fa45ae29c6574f46869bf84438eab_l3.png)
We know, area of triangle = ½ x Base x Height
Substituting th values we get,
1/2 x h x 18 = 71.43 cm
h = 7.92 cm
Question 11. Find the area of shaded region
Solution:

By Pythagoras theorem,
AB2 = AD2 + BD2
![Rendered by QuickLaTeX.com AB = \sqrt[]{AB^2 + BD^2} \\AB = \sqrt[]{12^2 + 16^2} \\AB = \sqrt[]{144 + 256} \\AB = \sqrt[]{400} AB = 20cm](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5db89cddf0975f49e56f07e57d36fcc6_l3.png)
In triangle ABC,
Perimeter = AB + BC + AC = 20cm + 52cm + 48cm
=120 cm
Now,
s = 120/2 = 60 cm
Area of the triangle by heron’s formula,
![Rendered by QuickLaTeX.com Area= \sqrt[]{60(60-20)(60-48)(60-52) } \\ =\sqrt[]{60 * 40 * 12 * 8} \\=\sqrt[]{(8 * 8 * 6 * 6 * 10 * 10)} \\=\sqrt[]{(8 * 6 * 10)^2} \\=480 sq. cm.](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0ec4a260791e317d7e35de4cef6c441b_l3.png)
Area of triangle ABD = 1/2(AD)(BD)
1/2 (12)(16) sq. cm. = 96 sq. cm.
Shaded area = area of triangle ABC – area of triangle ABD
= 480 – 96 sq. cm.
384 sq. cm.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...