Class 9 NCERT Solutions- Chapter 9 Areas of Parallelograms And Triangles – Exercise 9.3 | Set 2
Last Updated :
05 Apr, 2021
Question 11. In Figure, ABCDE is a pentagon. A line through B parallel to AC meets DC produced at F.

Show that
(i) ar(ΔACB) = ar(ΔACF)
(ii) ar(AEDF) = ar(ABCDE)
Solution:
(i) ΔACB and ΔACF lie on the same base AC and between the same parallels AC and BF.
Therefore,
ar(ΔACB) = ar(ΔACF)
(ii) ar(ΔACB) = ar(ΔACF)
=> ar(ΔACB)+ar(ΔACDE) = ar(ΔACF)+ar(ΔACDE)
=> ar(ABCDE) = ar(AEDF)
Question 12. A villager Itwaari has a plot of land of the shape of a quadrilateral. The Gram Panchayat of the village decided to take over some portion of his plot from one of the corners to construct a Health Centre. Itwaari agrees to the above proposal with the condition that he should be given equal amount of land in lieu of his land adjoining his plot so as to form a triangular plot. Explain how this proposal will be implemented.
Solution:

Let us assume ABCD be the plot of the land of the shape of a quadrilateral.
Construction:
Join the diagonal BD.
Draw AE parallel to BD.
Join BE, that intersected AD at O.

We will get,
ΔBCE is the shape of Itwari’s original field
ΔAOB is the area for construction of the Health Centre.
ΔDEO is the land joined to the plot.
To prove:
ar(ΔDEO) = ar(ΔAOB)
Proof:
ΔDEB and ΔDAB lie on the same base BD, in-between the same parallels BD and AE.
Therefore,
Ar(ΔDEB) = ar(ΔDAB)
=> ar(ΔDEB) – ar(ΔDOB) = ar(ΔDAB) – ar(ΔDOB)
=> ar(ΔDEO) = ar(ΔAOB)
Question 13. ABCD is a trapezium with AB || DC. A line parallel to AC intersects AB at X and BC at Y. Prove that ar (ΔADX) = ar (ΔACY).
[Hint: Join CX.]
Solution:

Given:
ABCD is a trapezium with,
AB || DC.
XY || AC
To Construct,
Join CX
Prove:
ar(ADX) = ar(ACY)
Proof:
ar(ΔADX) = ar(ΔAXC) -(equation 1)(Since they are on the same base AX and
in-between the same parallels AB and CD)
also,
ar(ΔAXC)=ar(ΔACY) -(equation-2)(Since they are on the same base AC and
in-between the same parallels XY and AC)
From equation (1) and (2),
ar(ΔADX) = ar(ΔACY)
Question 14. In Figure AP || BQ || CR. Prove that ar(ΔAQC) = ar(ΔPBR).
Solution:

Given:
AP || BQ || CR
Prove:
ar(AQC) = ar(PBR)
Proof:
ar(ΔAQB) = ar(ΔPBQ) -(equation 1)(Since they are on the same base BQ and
between the same parallels AP and BQ)
also,
ar(ΔBQC) = ar(ΔBQR) (equation 2)(Since they are on the same base BQ and
between the same parallels BQ and CR)
Adding equations (1) and (2),
ar(ΔAQB)+ar(ΔBQC) = ar(ΔPBQ)+ar(ΔBQR)
=> ar(ΔAQC) = ar(ΔPBR)
Question 15. Diagonals AC and BD of a quadrilateral ABCD intersect at O in such a way that ar(△AOD) = ar(△BOC). Prove that ABCD is a trapezium.
Solution:
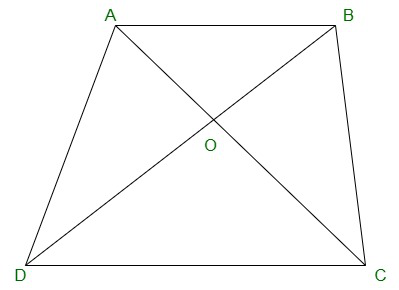
Given:
ar(ΔAOD) = ar(ΔBOC)
Prove:
ABCD is a trapezium.
Proof:
ar(ΔAOD) = ar(ΔBOC)
=> ar(ΔAOD) + ar(ΔAOB) = ar(ΔBOC)+ar(ΔAOB)
=> ar(ΔADB) = ar(ΔACB)
Areas of ΔADB and ΔACB are equal.
Therefore,
They should be lying between the same parallel lines.
Therefore,
AB ∥ CD
Hence, ABCD is a trapezium.
Question 16. In Figure, ar(DRC) = ar(DPC) and ar(BDP) = ar(ARC). Show that both the quadrilaterals ABCD and DCPR are trapeziums.

Solution:
Given:
ar(ΔDRC) = ar(ΔDPC)
ar(ΔBDP) = ar(ΔARC)
Prove:
ABCD and DCPR are trapeziums.
Proof:
ar(ΔBDP) = ar(ΔARC)
⇒ ar(ΔBDP) – ar(ΔDPC) = ar(ΔDRC)
⇒ ar(ΔBDC) = ar(ΔADC)
ar(ΔBDC) = ar(ΔADC).
Therefore,
ar(ΔBDC) and ar(ΔADC) are lying in-between the same parallel lines.
Hence, AB ∥ CD
ABCD is a trapezium.
Similarly,
ar(ΔDRC) = ar(ΔDPC).
Therefore,
ar(ΔDRC) and ar(ΔDPC) are lying in-between the same parallel lines.
Hence, DC ∥ PR
Thus, DCPR is a trapezium.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...