Class 9 NCERT Solutions- Chapter 10 Circles – Exercise 10.4
Last Updated :
03 Jan, 2021
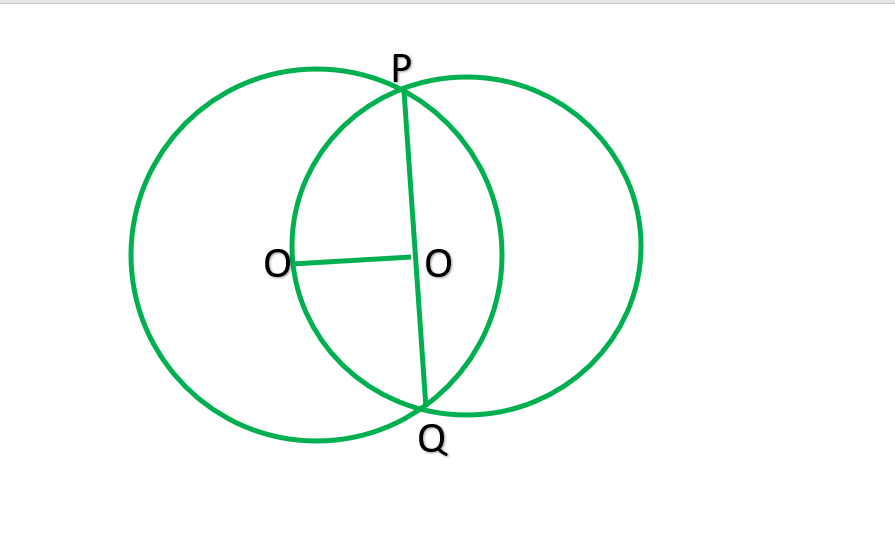
Question 1. Two circles of radii 5cm and 3cm intersect at two points and the distance between their centers is 4 cm. Find the length of the common chord.
Solution:
Given: OP=4cm, AP=3cm, QR=5cm
To find: In ∆APO:
AO²=5²=25
OP²=4²=16
AP²=3²=9
OP²+AP²=AO²
BY converse of Pythagoras theorem
ΔAPO: is a right ∠D=P
Now, in the bigger circle OP is perpendicular AB
AP=½AB —————-(perpendicular from the center of circle to a chord bisect the chord )
3=½AB
6=AB
∴Therefore the length of common chord is 6cm.
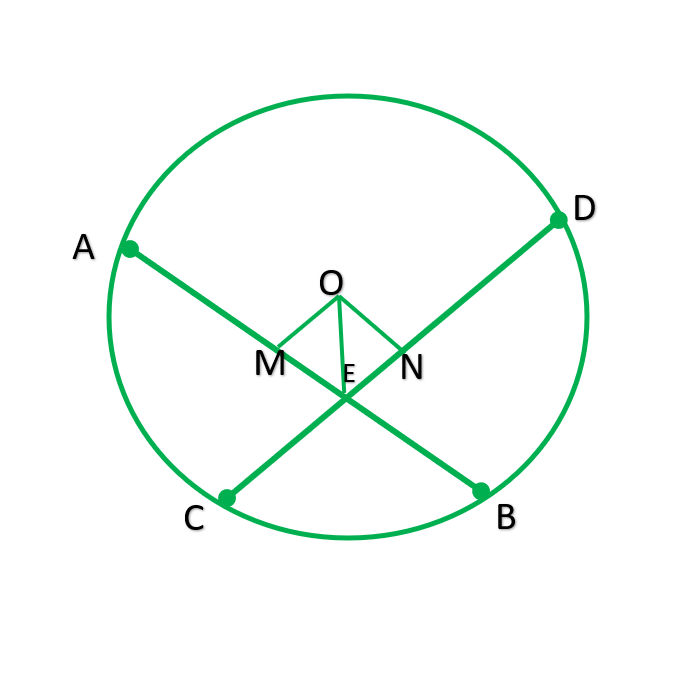
Question 2. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the center makes equal angles with the chords.
Solution:
Given: Equal chord AB & CD intersect at P.
To find: AP=PD and PB=PC
Construction: Draw OM perpendicular AB ,ON perpendicular CD and join OP.
Because perpendicular from center bisect the chord
∴AM=MB=½AB also CN=ND=½CD
AM=MB=CN=ND ——————1
Now, In ∆OMP and ∆ONP
ANGLE M=ANGLE N [90° both]
OP=OP [COMMON]
ON=OM [equal chords are equilateral from center]
∴∆OMP≅∆ONP
Therefore MP=PN (C.P.C.T.) ——————2
i)from 1 and 2
AM+MP=ND+AN
AP=PD
ii)MB-MP=CN=PN
PB=PC
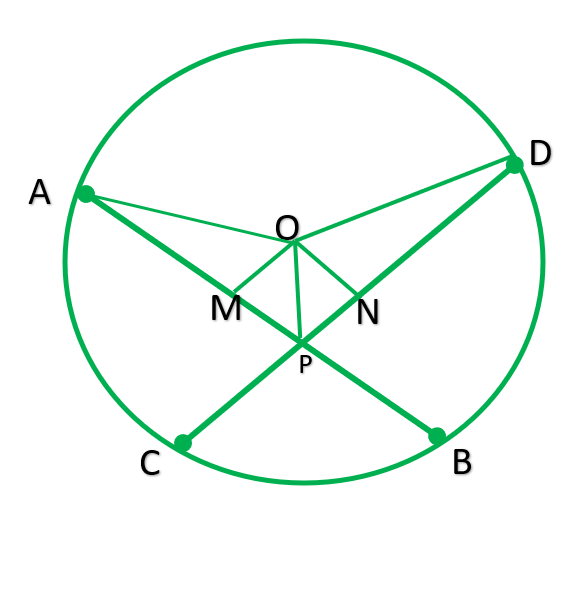
Question 3. If two equal chords of a circle intersect within the circle, prove that the line joining the point of intersection to the Centre makes equal angles with the chords.
Solution:
Given: Equal chords AB and CD intersect at P.
To prove: angle1=angle=2
Construction: Draw OM perpendicular AB & ON perpendicular CD.
Solution: In ∆OMP & ∆ONP
Angle M= Angel N [90 ° each]
OP=OP [common]
OM=ON —————[ Equal chords are equal distant from center]
∴∆OMP≅∆ONP ———-[R.H.S]
∴∠1=∠2 ———–[C.P.C.T]
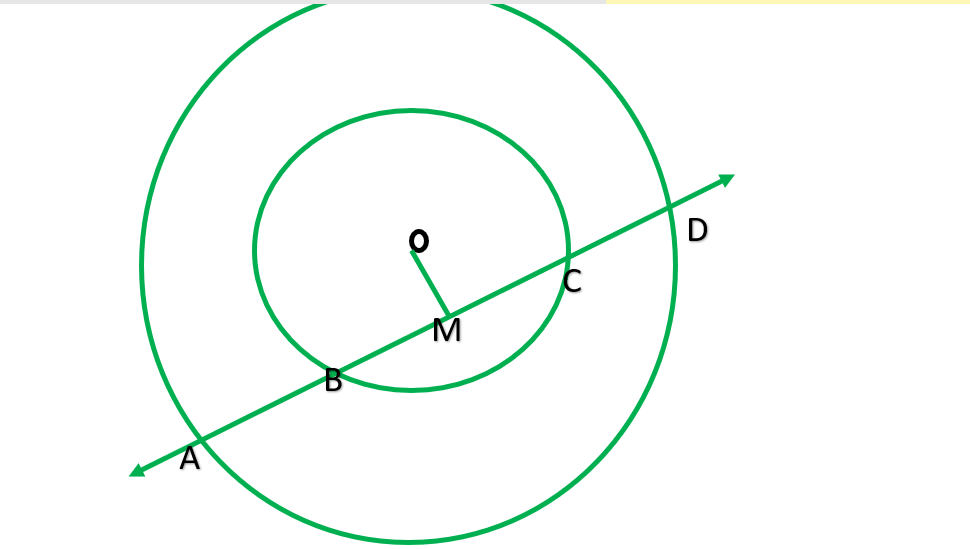
Question 4. If a line intersects two concentric circles (circles with the same centre) with centre O at A, B, C and D, prove that AB = CD (see Figure).
Solution:
Given : two concentric circle with O. A line intersect them at A, B, C , and D
To prove: AB=CD
construction: Draw OM ⊥ AD ,In bigger circle AD is chord OM ⊥ AD.
∴AM=MD —————-[⊥ from center of circle of a circle bisects the chord] __________ 1
The smaller circle :
BC is chord OM ⊥ BC
BM=MC ——————-[⊥ from center of circle of a circle bisects the chord] __________ 2
subtracting 1-2
AM-BM=MD-MC
AB=CD
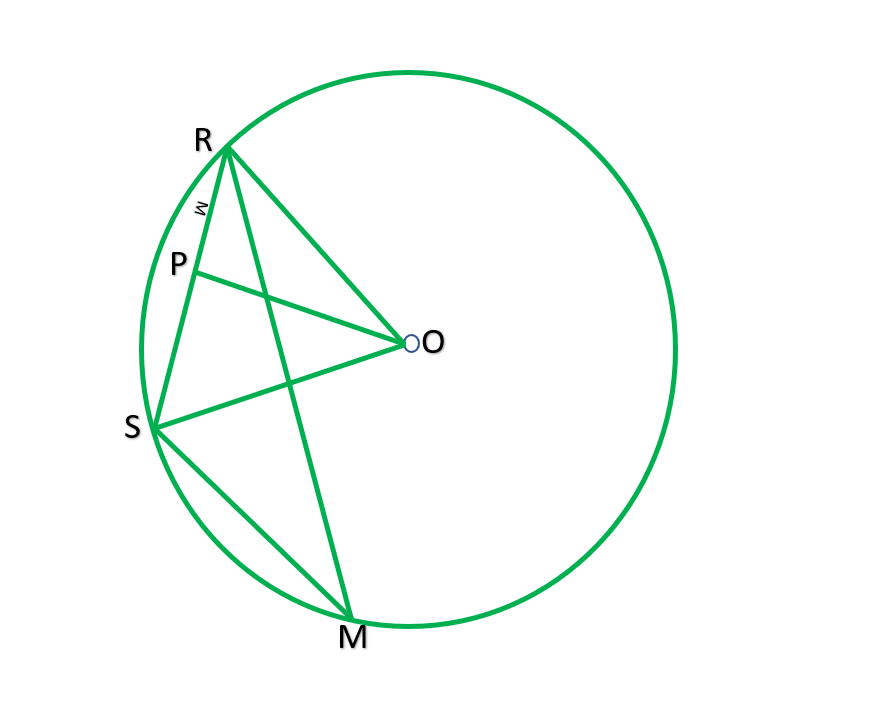
Question 5. Three girls Reshma, Salma and Mandip are playing a game by standing on a circle of radius 5m drawn in a park. Reshma throws a ball to Salma, Salma to Mandip, Mandip to Reshma. If the distance between Reshma and Salma and between Salma and Mandip is 6m each, what is the distance between Reshma and Mandip?
Solution:
To find RM=?
Let Reshma, Salma and Mandip be R,S,M
Construction: Draw OP ⊥ RS join OR and OS.
RP=½RS ___________[⊥ from center bisects the chord]
RP=½*6=3m
In right ΔORP
OP²=OR²- PR²
OP= √ 5² -3²
=√259 =√16 =4
Area of ΔORS=½*RS*OP
=½*6*4=12m² —————–1
Now, ∠N=90°
Area of ΔORS=½*SO*RN
=½*SO*RN ——————-2
Above ,1=2
12=½*5*RN
12/5*2=RN
RN=4.8
RM=2*RN _________________[⊥ from center bisects the chord]
=2*4.8
9.6m
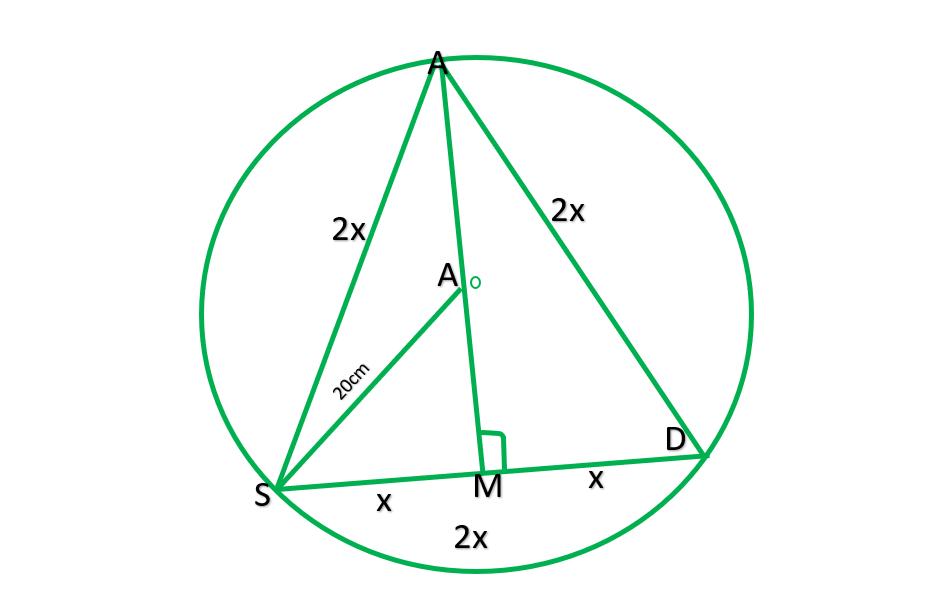
Question 6. A circular park of radius 20m is situated in a colony. Three boys Ankur, Syed and David are sitting at equal distance on its boundary. Each boy has toy telephone in his hand to talk with each other. Find the length of the string of each phone.
Solution:
Draw AM⊥SD
AS=SD=AD
∴ASD is the equilateral Δ
Let each side of Δ-2xm
SM=2x/2=x
Now in Δ DMS, by the Pythagoras theorem
AM²+SM²=AS²
AM²= AS²- SM²
AM=√(2x²+x² )
==√(3x² )
AM =√3x
OM=AM-AO
OM=√3x-20
Now in right ΔOMS
OM²+SM²=SO²
(√3x-20)²+2x²+x²=20²
20²+400-40√3x+x^2=400
4x²=40√3x
4xx=40√3x
X=(40√3)/4
X=10√3x
Length of each string =2x
=2*10√3xm
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...