Class 9 NCERT Solutions- Chapter 1 Number System – Exercise 1.3

Question 1. Write the following in decimal form and say what kind of decimal expansion each has :

(i) 36/100 

Solution:

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

36/100 = 0.36

(ii) 1/11 

Solution:

In the given question, we get

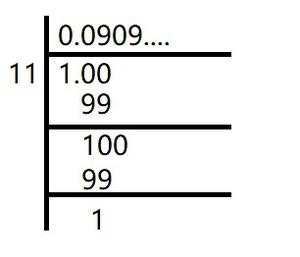
Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

1/11 =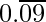 

(iii)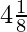 

Solution:

Here,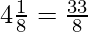 

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

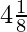 = 4.125

(iv) 3/13 

Solution:

In the given question, we get

Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

3/13 =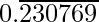 

(v) 2/11 

Solution:

In the given question, we get

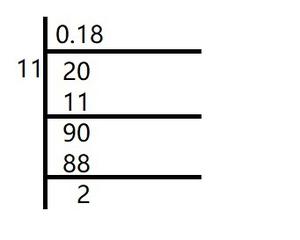
Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

2/11 =

(vi) 329/400 

Solution:

In the given question, we get

Here, the remainder becomes zero.

Hence, decimal expansion becomes terminating.

329/400 = 0.8225

Question 2. You know that 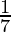= 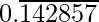Can you predict what the decimal expansions of 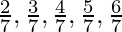are, without actually doing the long division? If so, how?

[Hint: Study the remainders while finding the value of 1/7 carefully.]

Solution:

As it is given,

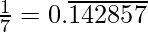
So, 

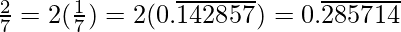
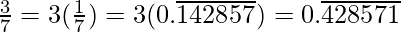
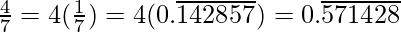
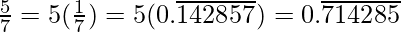
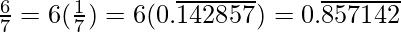
Question 3: Express the following in the form p/q, where p and q are integers and q ≠ 0.

(i)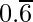 

Solution:

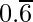= 0.66666……

Lets’s take, x = 0.66666……

10x = 6.666….

So, 

10x – x = (6.6666…..) – (0.66666……..)

9x = 6

x = 6/9 

x = 2/3 

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

(ii)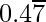 

Solution:

 = 0.4777777……

Lets’s take, x = 0.4777777……

10x = 4.77777…….

So,

10x – x = (4.77777…….) – (0.4777777……)

9x = 4.3

9x = 43/10 

x = 43/90

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

(iii)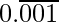 

Solution:

 = 0.001001001……

Lets’s take, x = 0.001001001……

1000x = 1.001001001……

So,

1000x – x = (1.001001001……) – (0.001001001……)

999x = 1

x = 1/999

Hence, x is in the form p/q, here p and q are integers and q ≠ 0.

Question 4. Express 0.99999 …. in the form p/q, Are you surprised by your answer? With your teacher and classmates discuss why the answer makes sense.

Solution:

Lets’s take, x = 0.99999……

10x = 9.99999….

So,

10x – x = (9.99999…..) – (0.99999……..)

9x = 9

x = 1

As, 0.9999….. just goes on, then at some point of time there is no gap between 1 and 0.9999….

We can observe that, 0.999 is too much near 1, hence, 1 is justified as the answer.

Hence, x is in the form p/q, where p and q are integers and q ≠ 0.

Question 5. What can the maximum number of digits be in the repeating block of digits in the decimal expansion of 1/17? Perform the division to check your answer.

Solution:

In the given question,

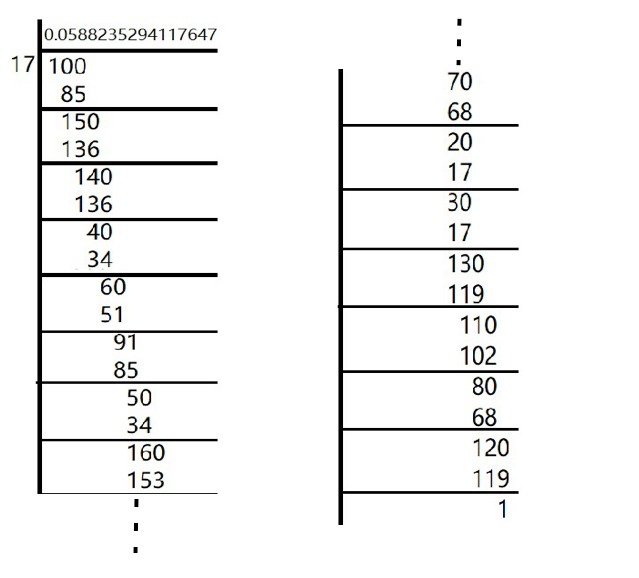
There are 16 digits in the repeating block of the decimal expansion of 1/17

Here, the remainder never becomes zero and remainders repeat after a certain stage.

Hence, decimal expansion is non-terminating recurring

1/17 =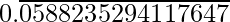 

Question 6. Look at several examples of rational numbers in the form p/q (q ≠ 0), where p and q are integers with no common factors other than 1 and having terminating decimal representations (expansions). Can you guess what property q must satisfy?

Solution:

We observe that when q is 2, 4, 5, 8, 10… Then the decimal expansion is terminating. 

Let’s take some example,

1/2 = 0. 5, denominator q = 2¹

7/8 = 0. 875, denominator q =2³

4/5 = 0. 8, denominator q = 5¹

So, we conclude that terminating decimal may be obtained in the situation where 

prime factorization of the denominator of the given fractions has the power 

of only 2 or only 5 or both.

In the form of 2^m × 5ⁿ, where n, m are natural numbers.

Question 7. Write three numbers whose decimal expansions are non-terminating non-recurring.

Solution:

As we know that all irrational numbers are non-terminating non-recurring. 

So,

√5 = 2.23606798…….

√27 =5.19615242……

√41 = 6.40312424…..

Question 8. Find three different irrational numbers between the rational numbers 5/7 and 9/11.

Solution:

As, decimal expansion of

5/7 =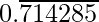 

9/11 =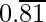 

Hence, three different irrational numbers between them can be as follows,

0.73073007300073000073…

0.75075007300075000075…

0.76076007600076000076…

Question 9. Classify the following numbers as rational or irrational :

(i) √23 

Solution:

√23 = 4.79583152……

As the number is non-terminating non-recurring.

It is an irrational number.

(ii) √225

Solution:

√225 = 15 = 15/1 

As the number can be represented in p/q form, where q ≠ 0.

It is a rational number.

(iii) 0.3796

Solution:

As, the number 0.3796, is terminating.

It is a rational number.

(iv) 7.478478…

Solution:

As, the number 7.478478, is non-terminating but recurring.

It is a rational number.

(v) 1.101001000100001…

Solution:

As, the number 1.101001000100001…, is non-terminating but recurring.

It is a rational number.