Class 8 RD Sharma Solutions – Chapter 8 Division Of Algebraic Expressions – Exercise 8.5
Last Updated :
11 Feb, 2021
Question 1: Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:
(i) 3x2 + 4x + 5, x – 2
Solution:
3x2 + 4x + 5, x – 2
By using factorization method,
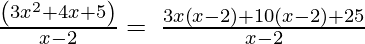
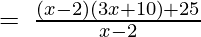 (Taking common (x-2) factor)
(Taking common (x-2) factor)
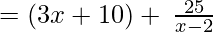
∴ the Quotient is 3x + 10 and the Remainder is 25.
(ii) 10x2 – 7x + 8, 5x – 3
Solution:
10x2 – 7x + 8, 5x – 3
By using factorization method,
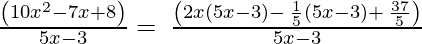
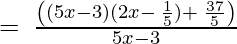 (Taking common (5x-3) factor)
(Taking common (5x-3) factor)
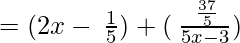
∴ the Quotient is (2x – 1/5) and the Remainder is 37/5.
(iii) 5y3 – 6y2 + 6y – 1, 5y – 1
Solution:
5y3 – 6y2 + 6y – 1, 5y – 1
By using factorization method,
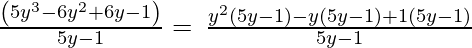
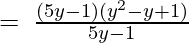 (Taking common (5y-1) factor)
(Taking common (5y-1) factor)
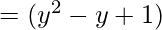
∴ the Quotient is (y2 – y + 1) and the Remainder is 0.
(iv) x4 – x3 + 5x, x – 1
Solution:
x4 – x3 + 5x, x – 1
By using factorization method,
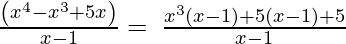
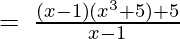 (Taking common (x-1) factor)
(Taking common (x-1) factor)
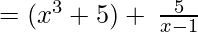
∴ the Quotient is x3 + 5 and the Remainder is 5.
(v) y4 + y2, y2 – 2
Solution:
y4 + y2, y2 – 2
By using factorization method,
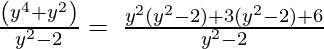
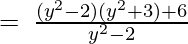 (Taking common (y2-2) factor)
(Taking common (y2-2) factor)
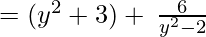
∴ the Quotient is y2 + 3 and the Remainder is 6.
Question 2: Find whether or not the first polynomial is a factor of the second:
(i) x + 1, 2x2 + 5x + 4
Solution:
x + 1, 2x2 + 5x + 4
Let us perform factorization method,
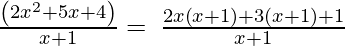
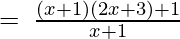 (Taking common (x+1) factor)
(Taking common (x+1) factor)
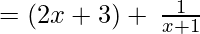
Since remainder is 1, therefore the first polynomial is not a factor of the second polynomial.
(ii) y – 2, 3y3 + 5y2 + 5y + 2
Solution:
y – 2, 3y3 + 5y2 + 5y + 2
Let us perform factorization method,
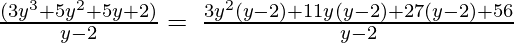
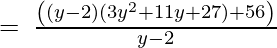 (Taking common (y-2) factor)
(Taking common (y-2) factor)
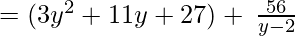
Since remainder is 56 therefore the first polynomial is not a factor of the second polynomial.
(iii) 4x2 – 5, 4x4 + 7x2 + 15
Solution:
4x2 – 5, 4x4 + 7x2 + 15
Let us perform factorization method,
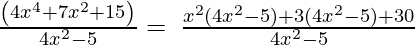
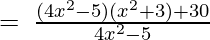 (Taking common (4x2-5) factor)
(Taking common (4x2-5) factor)
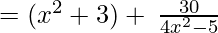
Since remainder is 30 therefore the first polynomial is not a factor of the second polynomial.
(iv) 4 – z, 3z2 – 13z + 4
Solution:
4 – z, 3z2 – 13z + 4
Let us perform factorization method,
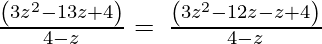
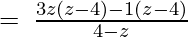 (Taking common (z-4) factor)
(Taking common (z-4) factor)
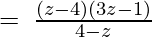
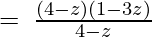
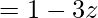
Since remainder is 0 therefore the first polynomial is a factor of the second polynomial.
(v) 2a – 3, 10a2 – 9a – 5
Solution:
2a – 3, 10a2 – 9a – 5
Let us perform factorization method,
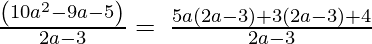
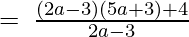 (Taking common (2a-3) common)
(Taking common (2a-3) common)
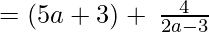
Since remainder is 4 therefore the first polynomial is not a factor of the second polynomial.
(vi) 4y + 1, 8y2 – 2y + 1
Solution:
4y + 1, 8y2 – 2y + 1
Let us perform factorization method,
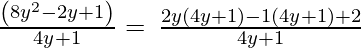
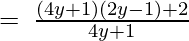 (Taking common (4y+1) factor)
(Taking common (4y+1) factor)
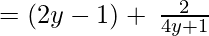
Since remainder is 2 therefore the first polynomial is not a factor of the second polynomial.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...