Class 8 RD Sharma Solutions – Chapter 8 Division Of Algebraic Expressions – Exercise 8.5

Question 1: Divide the first polynomial by the second polynomial in each of the following. Also, write the quotient and remainder:

(i) 3x² + 4x + 5, x – 2

Solution:

3x² + 4x + 5, x – 2

By using factorization method,

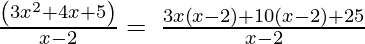
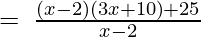                                                     (Taking common (x-2) factor)

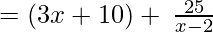
∴ the Quotient is 3x + 10 and the Remainder is 25.

(ii) 10x² – 7x + 8, 5x – 3

Solution:

10x² – 7x + 8, 5x – 3

By using factorization method,

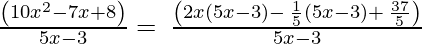
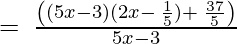                                              (Taking common (5x-3) factor) 

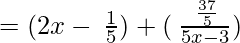
∴ the Quotient is (2x – 1/5) and the Remainder is 37/5.

(iii) 5y³ – 6y² + 6y – 1, 5y – 1

Solution:

5y³ – 6y² + 6y – 1, 5y – 1

By using factorization method,

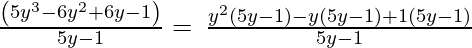
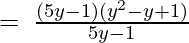                                                    (Taking common (5y-1) factor)

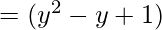
∴ the Quotient is (y² – y + 1) and the Remainder is 0.

(iv) x⁴ – x³ + 5x, x – 1

Solution:

x⁴ – x³ + 5x, x – 1

By using factorization method,

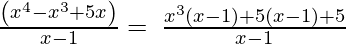
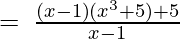                                                       (Taking common (x-1) factor)

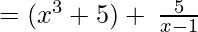
∴ the Quotient is x³ + 5 and the Remainder is 5.

(v) y⁴ + y², y² – 2

Solution:

y⁴ + y², y² – 2

By using factorization method,

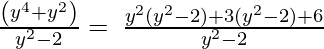
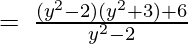                                                          (Taking common (y²-2) factor)

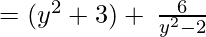
∴ the Quotient is y² + 3 and the Remainder is 6.

Question 2: Find whether or not the first polynomial is a factor of the second:

(i) x + 1, 2x² + 5x + 4

Solution:

x + 1, 2x² + 5x + 4

Let us perform factorization method,

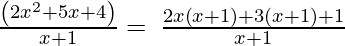
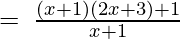                                                                   (Taking common (x+1) factor)

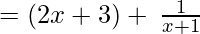
Since remainder is 1, therefore the first polynomial is not a factor of the second polynomial.

(ii) y – 2, 3y³ + 5y² + 5y + 2

Solution:

y – 2, 3y³ + 5y² + 5y + 2

Let us perform factorization method,

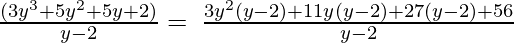
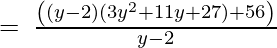                                                        (Taking common (y-2) factor)

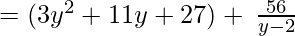
Since remainder is 56 therefore the first polynomial is not a factor of the second polynomial.

(iii) 4x² – 5, 4x⁴ + 7x² + 15

Solution:

4x² – 5, 4x⁴ + 7x² + 15

Let us perform factorization method,

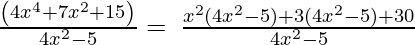
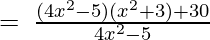                                                                      (Taking common (4x²-5) factor)

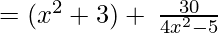
Since remainder is 30 therefore the first polynomial is not a factor of the second polynomial.

(iv) 4 – z, 3z² – 13z + 4

Solution:

4 – z, 3z² – 13z + 4

Let us perform factorization method,

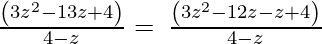
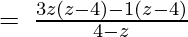                                                                     (Taking common (z-4) factor)

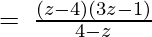
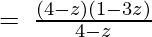
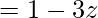
Since remainder is 0 therefore the first polynomial is a factor of the second polynomial.

(v) 2a – 3, 10a² – 9a – 5

Solution:

2a – 3, 10a² – 9a – 5

Let us perform factorization method,

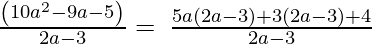
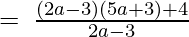                                                                    (Taking common (2a-3) common)

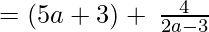
Since remainder is 4 therefore the first polynomial is not a factor of the second polynomial.

(vi) 4y + 1, 8y² – 2y + 1

Solution:

4y + 1, 8y² – 2y + 1

Let us perform factorization method,

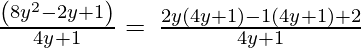
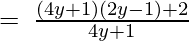                                                                   (Taking common (4y+1) factor)

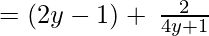
Since remainder is 2 therefore the first polynomial is not a factor of the second polynomial.