Class 8 RD Sharma Solutions – Chapter 5 Playing with Numbers – Exercise 5.3
Last Updated :
11 Dec, 2020
Solve each of the following Cryptarithms:
Question 1.
3 7
+ A B
9 A
Solution:
In the unit’s place,
7 + B = A
In the ten’s place,
3 + A = 9
From ten’s place A = 6 then B = −1
Hence, it is not possible
Thus, there should be one carry in ten’s place
7 + B > 9
Solve for ten’s place with one carry,
3 + A + 1 = 9
A = 9−1−3 = 5
In unit’s place subtracting 10 as one carry is given to ten’s place,
7 + B – 10= 5
B = 5 + 10 − 7 = 8
Therefore,
A = 5 and B = 8
Question 2.
A B
+ 3 7
9 A
Solution:
In the unit’s place,
B + 7 = A
In the ten’s place,
A + 3 = 9
From ten’s place A = 6 and B = −1
It is not possible.
Thus there should be one carry in ten’s place, which means B + 7 > 9
Solve for ten’s place with one carry,
A + 3 + 1 = 9
A = 9 − 4 = 5
In unit’s place subtracting 10 as one carry is given to ten’s place,
B + 7 – 10 = 5
B = 5 + 10 − 7 = 8
Therefore,
A = 5 and B = 8
Question 3.
A 1
+ 1 B
B 0
Solution:
In the unit’s place,
1 + B = 0
Thus B = -1
Which is not possible.
Thus, there should be one carry in ten’s place,
A + 1 + 1 = B —-> (equation 1)
For unit’s place, we need to subtract 10 as one carry is given in ten’s place,
1 + B – 10 = 0
B = 10 − 1 = 9
Substituting B = 9 in (equation 1),
A + 1 + 1 = 9
A = 9 − 1 − 1 = 7
Therefore, A = 7 and B = 9
Question 4.
2 A B
+ A B 1
B 1 8
Solution:
In the unit’s place,
B + 1 = 8
B = 7
In the ten’s place,
A + B = 1
A + 7 = 1
A = −6
Which is not possible.
Hence, A + B > 9
We know that now there should be one carry in hundred’s place, and so we need to subtract 10 from ten’s place,
That is,
A + B – 10 = 1
A + 7 = 11
A = 11 − 7 = 4
Now to check whether our values of A and B are correct, we should solve for hundred’s place.
2 + A + 1 = B
2 + 4 + 1 = 7
7 = 7
Hence,
RHS = LHS
Therefore,
A = 4 and B = 7
Question 5.
1 2 A
+ 6 A B
A 0 9
Solution:
In the unit’s place,
A + B = 9 —-> (equation 1)
With this condition we know that sum of 2 digits can be greater than 18.
So, there is no need to carry one from ten’s place.
In the ten’s place,
2 + A = 0
Which means A = −2
Which is not possible
Hence,
2 + A > 9
Now, there should be one carry in hundred’s place and hence we need to subtract 10 from ten’s place,
That is,
2 + A – 10 = 0
A = 10 − 2 = 8
Now, substituting A=8 in (equation 1),
A + B = 9
8 + B = 9
B = 9 – 8
B = 1
Therefore,
A = 8 and B = 1
Question 6.
A B 7
+ 7 A B
A 0 9
Solution:
In the unit’s place,
The two conditions are,
(i) 7 + B ≤ 9
(ii) 7 + B > 9
For 7 + B ≤ 9
7 + B = A
A – B = 7 —->(equation 1)
In the ten’s place,
B + A = 8 —-> (equation 2)
Solve equation 1 and equation 2,
2A = 15 which means A = 7.5
Which is not possible
Thus, first condition 7 + B ≤ 9 is wrong.
Therefore,
7 + B > 9 is correct condition
Hence, there should be one carry in ten’s place and subtracting 10 from unit’s place,
7 + B – 10 = A
B – A = 3 —-> (equation 3)
In the ten’s place,
B + A + 1 = 8
B + A = 8 − 1
B + A = 7 —-> (equation 4)
Solve equation 3 and equation 4,
2B = 10
B = 10 = 5
2
Substituting the value of B in equation 4
B + A = 7
5 + A = 7
A = 7 − 5 = 2
Therefore,
B = 5 and A = 2
Question 7. Show that the Cryptarithm does not have any solution.
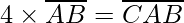
Solution:
If B is multiplied by 4 then only 0 satisfies the above condition.
So, for unit place to satisfy the above condition, we should have B = 0.
In ten’s place, only 0 satisfies the above condition.
But, AB cannot be 00 as 00 is not a two digit number.
So, A and B cannot be equal to 0
Therefore,
There is no solution satisfying the condition
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...