Class 8 RD Sharma Solutions – Chapter 14 Compound Interest – Exercise 14.4 | Set 2
Last Updated :
06 Oct, 2022
Question 11. 6400 workers were employed to construct a river bridge in four years. At the end of the first year, 25% workers were retrenched. At the end of the second year, 25% of those working at that time were retrenched. However, to complete the project in time, the number of workers was increased by 25% at the end of the third year. How many workers were working during the fourth year?
Solution:
We have,
Initial number of workers are = 6400
At the end of first year = 25% retrenched
At the end of second year = 25% retrenched
At the end of third year = 25% increased
By using the formula,
A = P (1 + 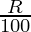 )
)
Substituting the values, we have
x = 6400 (1 –  ) (1 –
) (1 –  ) (1 +
) (1 +  )
)
= 6400 (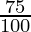 ) (
) (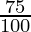 ) (
) ( )
)
= 6400 (0.75) (0.75) (1.25)
= 4500
Therefore,
Number of workers working during the fourth year is 4500.
Question 12. Aman started a factory with an initial investment of Rs 100000. In the first year, he incurred a loss of 5%. However, during the second year, he earned a profit of 10% which in the third year rose to 12%. Calculate his net profit for the entire period of three years.
Solution:
We have,
Initial investment by Aman = Rs.100000
In first year = incurred a loss of 5%
In second year = earned a profit of 10%
In third year = earned a profit of 12 %
By using the formula,
A = P (1 + 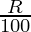 )
)
Substituting the values, we have
x = 100000 (1 –  ) (1 +
) (1 + 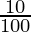 ) (1 +
) (1 + 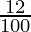 )
)
= 100000 (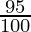 ) (
) (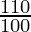 ) (
) (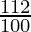 )
)
= 100000 (0.95) (1.1) (1.12)
= 117040
Therefore,
Aman’s net profit for entire three years is 117040 – 100000 = Rs 17040.
Question 13. The population of a town increases at the rate of 40 per thousand annually. If the present population be 175760, what was the population three years ago.
Solution:
We have,
Annual increase rate of population of town = 40/1000× 100 = 4%
Present population of town = 175760
So, let the population of town 3 years ago be = x
By using the formula,
A = P (1 + 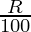 )
)
Substituting the values, we have
175760 = x (1 + 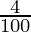 ) (1 +
) (1 + 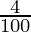 ) (1 +
) (1 + 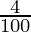 )
)
175760 = x (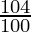 ) (
) (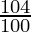 (
(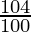
175760 = x (1.04) (1.04) (1.04)
175760 = 1.124864x
x = 175760/1.124864
= 156250
Therefore,
Population 3 years ago was 156250.
Question 14. The population of a mixi company in 1996 was 8000 mixies. Due to increase in demand it increases its production by 15% in the next two years and after two years its demand decreases by 5%. What will its production after 3 years?
Solution:
We have,
Population of mixi company in 1996 was = 8000 mixies
Production growth rate in next 2 years is = 15 %
Decrease rate in 3rd year is = 5%
By using the formula,
A = P (1 + 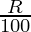 )
)
Substituting the values, we have
x = 8000 (1 + 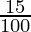 ) (1 +
) (1 + 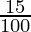 ) (1 –
) (1 –  )
)
= 8000 (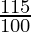 0) (
0) (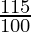 ) (
) (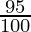 )
)
= 8000 (1.15) (1.15) (0.95)
= 10051
Therefore,
Production after three years will be 10051 mixies.
Question 15. The population of a city increases each year by 4% of what it had been at the beginning of each year. If the population in 1999 had been 6760000, find the population of the city in (1) 2001 (ii) 1997.
Solution:
We have,
Annual increase rate of population of city is = 4%
Population in 1999 was = 6760000
(i) Population of the city in 2001 (2 years after)
By using the formula,
A = P (1 + 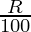 )
)
Substituting the values, we have
x = 6760000 (1 + 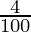 ) (1 +
) (1 + 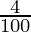 )
)
= 6760000 (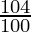 ) (
) (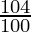 )
)
= 6760000 (1.04) (1.04)
= 7311616
Therefore,
Population in the year 2001 is 7311616
(ii) Population of city in 1997 (2 years ago)
By using the formula,
A = P (1 + 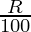 )
)
Substituting the values, we have
x = 6760000 (1 – 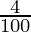 ) (1 –
) (1 – 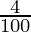 )
)
= 6760000 (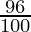 ) (
) (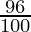 )
)
= 6760000 (0.96) (0.96)
= 6230016
Therefore,
Population in the year 1997 was 6230016.
Question 16. Jitendra set up a factory by investing Rs. 2500000. During the first two successive years his profits were 5% and 10% respectively. If each year the profit was on previous year’s capital, compute his total profit.
Solution:
We have,
Initial investment by Jitendra was = Rs 2500000
Profit in first 2 successive years were = 5% and 10%
Final investment after two successive profits = 2500000 (1 +  ) (1 +
) (1 + 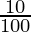 )
)
= 2500000 (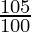 ) (
) (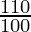 )
)
= 2500000 (1.05) (1.1)
= 2887500
Therefore,
Jitendra total profit is = 2887500 – 2500000 = Rs 387500.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...