Class 8 RD Sharma Solutions – Chapter 14 Compound Interest – Exercise 14.4 | Set 1

Question 1. The present population of a town is 28000. If it increases at the rate of 5% per annum, what will be its population after 2 years?

Solution:

We have,

Present population of town is = 28000

Rate of increase in population is = 5% per annum

Number of years = 2

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

Population of town after 2 years = 28000 (1 + 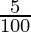)²

= 28000 (1.05)²

= 30870

Therefore,

Population of town after 2 years will be 30870.

Question 2. The population of a city is 125000. If the annual birth rate and death rate are 5.5% and 3.5% respectively, calculate the population of city after 3 years.

Solution:

We have,

Population of city (P) = 125000

Annual birth rate R1= 5.5 %

Annual death rate R2 = 3.5 %

Annual increasing rate R = (R1 – R2) = 5.5 – 3.5 = 2 %

Number of years = 3

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

So, population after two years is = 125000 (1 + 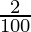)³

= 125000 (1.02)³

= 132651

Therefore,

Population after 3 years will be 132651.

Question 3. The present population of a town is 25000. It grows at 4%, 5% and 8% during first year, second year and third year respectively. Find its population after 3 years.

Solution:

We have,

Present population is = 25000

First year growth R1 = 4%

Second year growth R2 = 5%

Third year growth R3 = 8%

Number of years = 3

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

So, population after three years = P (1 + 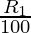) (1 + 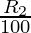) (1 + )

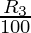= 25000(1 + 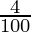) (1 + 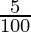) (1 + 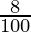0)

= 25000 (1.04) (1.05) (1.08)

= 29484

Therefore,

Population after 3 years will be 29484.

Question 4. Three years ago, the population of a town was 50000. If the annual increase during three successive years be at the rate of 4%, 5% and 3% respectively, find the present population.

Solution:

We have,

Three years ago population of town was = 50000

Annual increasing in 3 years = 4%,5%, 3% respectively

So, let present population be = x

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

x = 50000 (1 + 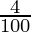) (1 + 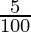) (1 + )

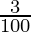= 50000 (1.04) (1.05) (1.03)

= 56238

Therefore,

Present population of the town is 56238.

Question 5. There is a continuous growth in population of a village at the rate of 5% per annum. If its present population is 9261, what it was 3 years ago?

Solution:

We have,

Present population of town is = 9261

Continuous growth of population is = 5%

So, let population three years ago be = x

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

9261 = x (1 + 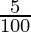) (1 + 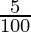) (1 + )

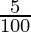9261 = x (1.05) (1.05) (1.05)

= 8000

Therefore,

Present population of the town is 8000.

Question 6. In a factory the production of scooters rose to 46305 from 40000 in 3 years. Find the annual rate of growth of the production of scooters.

Solution:

We have,

Initial production of scooters is = 40000

Final production of scooters is = 46305

Time = 3 years

Let annual growth rate be = R%

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

46305 = 40000 (1 + ) (1 + ) (1 + )

46305 = 40000 (1 + )³

(1 + )³ = 46305/40000

= 9261/8000

= (21/20)³

1 +  = 21/20

 = 21/20 – 1

 = (21-20)/20

= 1/20

R = 100/20

= 5

Therefore,

Annual rate of growth of the production of scooters is 5%.

Question 7. The annual rate of growth in population of a certain city is 8%. If its present population is 196830, what it was 3 years ago?

Solution:

We have,

Annual growth rate of population of city is = 8%

Present population of city is = 196830

Let population of city 3 years ago be = x

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

196830 = x (1 + 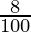) (1 + 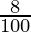) (1 + )

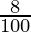196830 = x (27/25) (27/25) (27/25)

196830 = x (1.08) (1.08) (1.08)

196830 = 1.259712x

x = 196830/1.259712

= 156250

Therefore,

Population 3 years ago was 156250.

Question 8. The population of a town increases at the rate of 50 per thousand. Its population after 2 years will be 22050. Find its present population.

Solution:

We have,

Growth rate of population of town is = 50/1000×100 = 5%

Population after 2 years is = 22050

So, let present population of town be = x

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

22050 = x (1 + 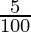) (1 + )

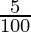22050 = x () ()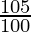

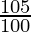22050 = x (1.05) (1.05)

22050 = 1.1025x

x = 22050/1.1025

= 20000

Therefore,

Present population of the town is 20000.

Question 9. The count of bacteria in a culture grows by 10% in the first hour, decreases by 8% in the second hour and again increases by 12% in the third hour. If the count of bacteria in the sample is 13125000, what will be the count of bacteria after 3 hours?

Solution:

Given details are,

Count of bacteria in sample is = 13125000

The increase and decrease of growth rates are = 10%, -8%, 12%

So, let the count of bacteria after 3 hours be = x

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

x = 13125000 (1 + 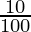) (1 – 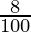) (1 + )

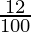x = 13125000 (110/100) (92/100) (112/100)

x = 13125000 (1.1) (0.92) (1.12)

= 14876400

Therefore,

Count of bacteria after three hours will be 14876400.

Question 10. The population of a certain city was 72000 on the last day of the year 1998. During next year it increased by 7% but due to an epidemic it decreased by 10% in the following year. What was its population at the end of the year 2000?

Solution:

We have,

Population of city on last day of year 1998 = 72000

Increasing rate (R) in 1999 = 7%

Decreasing rate (R) in 2000 = 10 %

By using the formula,

A = P (1 + )ⁿ

Substituting the values, we have 

x = 72000 (1 + 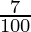) (1 – )

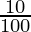= 72000 (107/100) (90/100)

= 72000 (1.07) (0.9)

= 69336

Therefore,

Population at the end of the year 2000 will be 69336.

Chapter 14 Compound Interest – Exercise 14.4 | Set 2