Class 12 RD Sharma Solutions – Chapter 7 Adjoint and Inverse of a Matrix – Exercise 7.1 | Set 3

Question 25. Show that the matrix A = 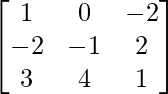 satisfies the equation A³ – A² – 3A – I₃ = 0. Hence, find A^-1.

Solution:

Here, A =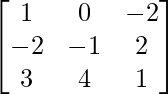 

A² =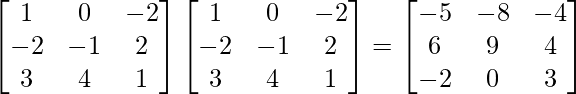 

A³ =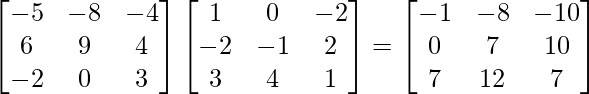 

Now A³ – A² – 3A – I₃ =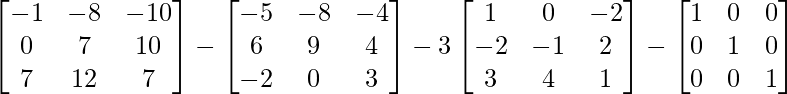 

=

= 

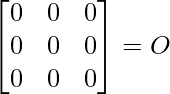
So, A³ – A² – 3A – I₃ = 0

⇒ A^-1(AAA) – A^-1(AA) – 3A^-1A – A^-1I = 0

⇒ A² – A – 3I – A^-1 = 0

⇒ A^-1 = A² – A – 3I

= 

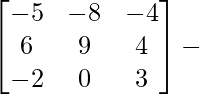
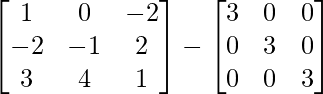
Therefore, A^-1 =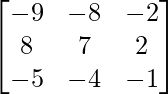

Question 26. If A = 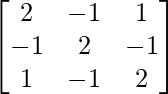. Verify that A³ – 6A² + 9A – 4I = O and hence find A^-1.

Solution:

Here, A =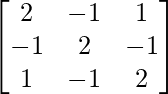 

A² =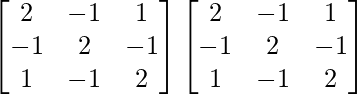 

=

= 

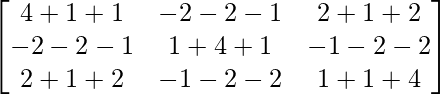
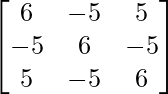
A³ = A²A =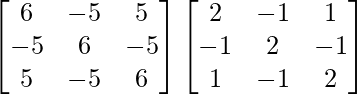 

= 

= 

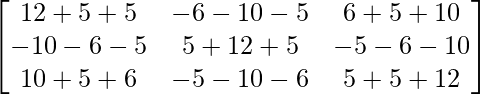
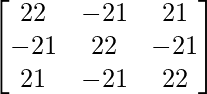
Now, A³ – 6A² + 9A – 4I

= 

= 

= 

= 

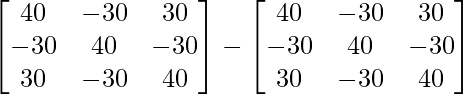
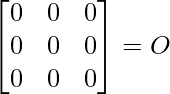
So, A³ – 6A² + 9A – 4I = O

Multiplying both side by A^-1

⇒ A^-1(AAA) – 6A^-1(AA) 9A^-1A – 4A^-1I = O

⇒ AAI – 6AI + 9I = 4A^-1

⇒ 4A^-1 = A²I – 6AI + 9I

=

=

=

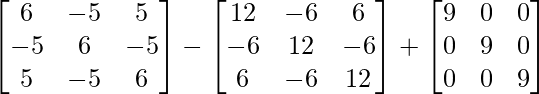
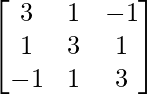
⇒ A^-1 =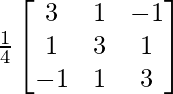 

Question 27. If A =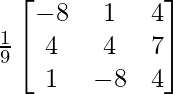, prove that A^-1 = A^T.

Solution:

Here, A =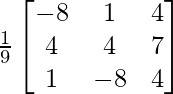 

A^T =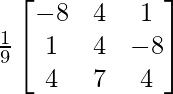 

Now, Finding A^-1

|A| = 1/9[-8(16 + 56) – 1(16 – 7) + 4(-32 – 4)]

= -81

 Therefore, inverse of A exists

Cofactors of A are:

C₁₁ = 72      C₁₂ = -9       C₁₃ = -36

C₂₁ = -36    C₂₂ = -36    C₂₃ = -63

C₃₁ = -9      C₃₂ = 72      C₃₃ = -36

adj A =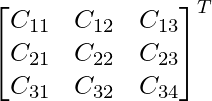 

=

=

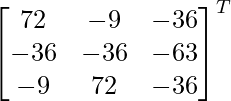
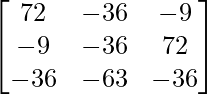
A^-1 = 1/|A|. adj A

Hence, A^-1 =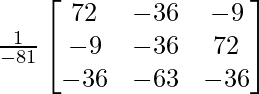 

= 

= A^T

Hence Proved   

Question 28. If A = 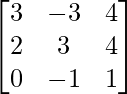, show that A^-1 = A³.

Solution:

Here, A =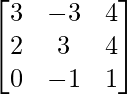 

|A| = 3(-3 + 4) + 3(2 – 0) + 4(-2 – 0)

= 3 + 6 – 8

= 1 

Therefore, inverse of A exists

Cofactors of A are:

C₁₁ = 1      C₁₂ = -2     C₁₃ = -2

C₂₁ = -1    C₂₂ = 3      C₂₃ = 3

C₃₁ = 0     C₃₂ = -4     C₃₃ = -3

adj A =

A^-1= 1/|A|. adj A

= 

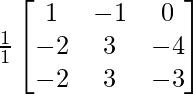
Now, A² =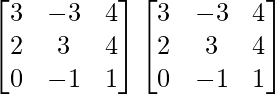 

=

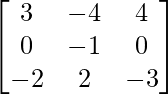
A³ =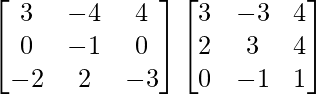 

=

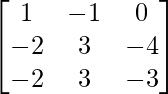
= A^-1

Hence Proved

Question 29. If A =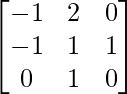, show that A² = A^-1.

Solution: 

Here, A =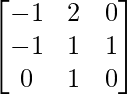 

LHS = A²

= 

= 

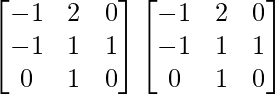
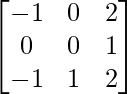
|A| = -1(1 – 0) – 2(-1 – 0) + 0

= 1

Therefore, inverse of A exists

Cofactors of A are:

C₁₁ = -1     C₁₂ = 0     C₁₃ = -1

C₂₁ = 0      C₂₂ = 0     C₂₃ = 1

C₃₁ = 21    C₃₂ = 1      C₃₃ = 1

adj A =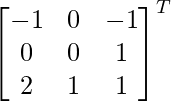 

=

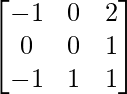
A^-1 = 1/|A|. adj A

Hence, A^-1 =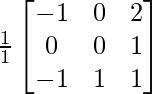 

=

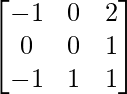
= A² 

Hence Proved

Question 30. Solve the matrix equation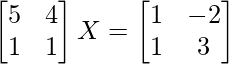, where X is a 2×2 matrix.

Solution:

We have,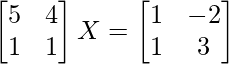 

Let A =  and B =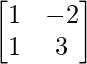 

So. AX = B

⇒ X = A^-1B

Now, |A| = 5 – 4 = 1 

Co factors of A are:

C₁₁ = 1         C₁₂ = -1

C₂₁ = -4      C₂₂ = 5

adj A =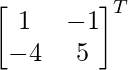 

=

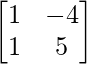
A^-1 =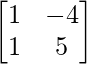 

Therefore, X =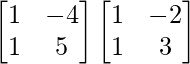 

X =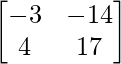 

Question 31. Find the matrix X satisfying the matrix equation: X.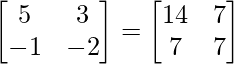

Solution:

We have,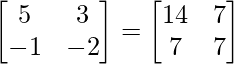 

Let A =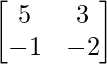and B =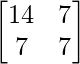 

So, XA = B

XAA^-1 = BA^-1

XI = BA^-1 ………..(i)

Now, |A| = -7

Co factors of A are:

C₁₁ = -2       C₁₂ = 1

C₂₁ = -3      C₂₂ = 5

adj A =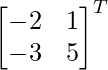 

=

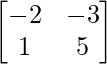
A^-1 = 1/|A|.adj (A)

=

Therefore, X =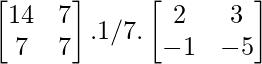 

=

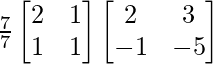
X =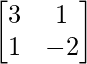 

Question 32. Find the matrix X for which: 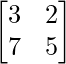X

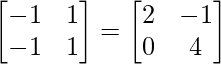
Solution:

Let, A = 

B =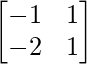 

C =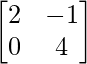 

 Then the given equation becomes

 A × B = C

⇒ X = A^-1CB^-1

Now |A| = 35 -14 = 21

|B| = -1 + 2 = 1

A^-1 = adj (A)/|A| =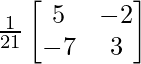 

B^-1 = adj (B)/|A| = 

X = A^-1 CB^-1 = 

= 

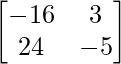
Question 33. Find the matrix X satisfying the equation: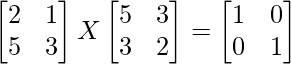

Solution:

Let A =  B =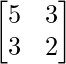 

AXB = I

X = A^-1B^-1

|A| = 6 – 5 = 1

|B| = 10 – 9 = 1

A^-1 = adj A /|A| =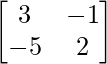 

B^-1 = adj B/|B| =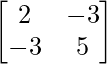 

X =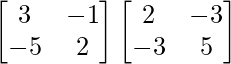 

= 

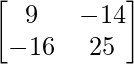
Question 34. If A = 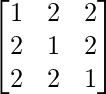, Find A^-1 and prove that A² – 4A – 5I = O.

Solution:

Here, A =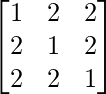 

A² =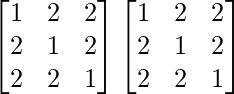 

= 

Now, A² + 4A – 5I

= 

= 

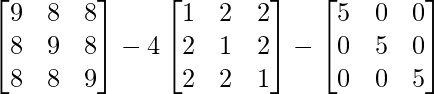
Now, A² – 4A – 5I = O

⇒ A^-1AA – 4A^-1A – 5A^-1I = O 

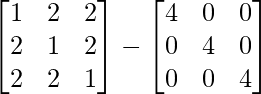
⇒ 5A^-1 = [A – 4I]

= 

= 

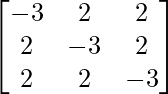
 A^-1 =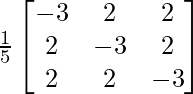 

Question 35. If A is a square matrix of order n, prove that |A adj A| = |A|ⁿ.

Solution:

Given, |A adj A| = |A|ⁿ

Taking LHS = |A Adj A|

= |A| |Adj A| 

= |A| |A|^n-1

= |A|^n-1+1

= |A|ⁿ = RHS 

Hence Proved

Question 36. If A^-1 = 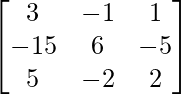 and B = 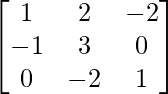, find (AB)^-1.

Solution:

Here, B =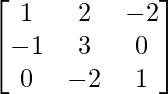 

|B| = 1(3 – 0) – 2(-1 – 0) – 2(2 – 0)

= 3 + 2 – 4 = 1

Therefore, inverse of B exists

Cofactors of B are:

C₁₁ = 3       C₁₂ = 1      C₁₃ = 2

C₂₁ = 2      C₂₂ = 1      C₂₃ = 2

C₃₁ = 6     C₃₂ = 2      C₃₃ = 5

adj A =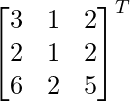 

= 

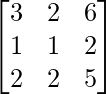
Therefore,

B^-1 =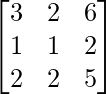 

Hence, (AB)^-1 = B^-1A^-1

= 

= 

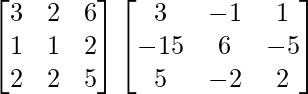
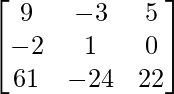
Question 37. If A = 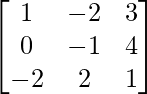, find (A^T)^-1.

Solution:

Assuming B = A^T =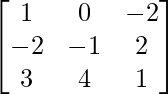 

|B| = 1(-1 – 8) – 0 – 2(-8 + 3)

= -9 + 10 = 1

Therefore, inverse of B exists

Cofactors of B are:

C₁₁ = -9      C₁₂ = 8      C₁₃ = -5

C₂₁ = -8     C₂₂ = 7      C₂₃ = -4

C₃₁ = -2     C₃₂ = 2      C₃₃ = -1

adj B =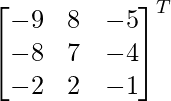 

=

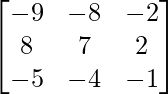
B^-1 =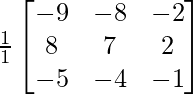 

or (A^T)^-1 =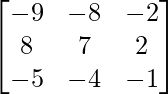 

Question 38. Find the adjoint of the matrix A = 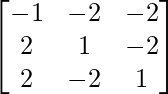and hence show that A (adj A) = |A|I₃.

Solution:

Here, A =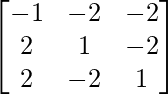 

|A| = -1(1 – 4) – 2(2 + 4) – 2(-4 – 2)

= 3 + 12 + 12 = 27

Therefore, inverse of A exists

Cofactors of A are:

C₁₁ = -3     C₁₂ = -6      C₁₃ = -6

C₂₁ = 6      C₂₂ = 3       C₂₃ = -6

C₃₁ = 6      C₃₂ = -6      C₃₃ = 3

adj A =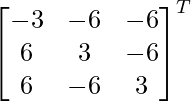 

= 

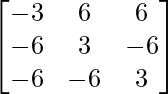
A (adj A) =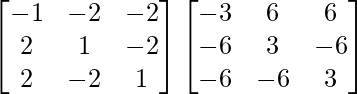 

= 

or A (adj A) = 27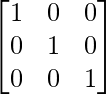

Hence, A (adj A) = |A|I₃ 

Hence Proved

Question 39. If A = 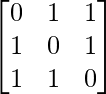, A^-1 and show that A^-1 = 1/2(A² – 3I).

Solution:

Here, A = 

|A| = 0 – 1(0 – 1) + 1(1 – 0)

= 1 + 1 = 2

Therefore, inverse of A exists

Cofactors of A are:

C₁₁ = -1     C₁₂ = 1      C₁₃ = 1

C₂₁ = 1      C₂₂ = -1    C₂₃ = 1

C₃₁ = 1      C₃₂ = 1      C₃₃ = -1

adj A =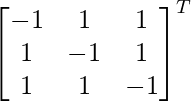 

= 

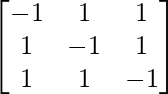
A^-1 = 1/|A|. adj A

Hence, A^-1 =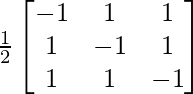 

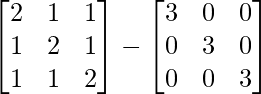
Now, A² – 3I = 

=

=

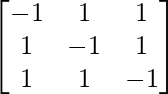
Hence, A^-1 = 1/2(A² – 3I) 

Hence Proved