Class 12 RD Sharma Solutions – Chapter 7 Adjoint and Inverse of a Matrix – Exercise 7.1 | Set 1
Last Updated :
28 Mar, 2021
Question 1. Find the adjoint of the following matrices:
Verify that (adj A)A = |A|I = A(adj A) for the above matrices:
(i) 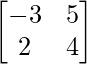
Solution:
Here, A = 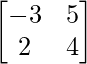
Cofactors of A are:
C11 = 4 C12 = -2
C21 = -5 C22 = -3
adj A =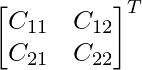
(adj A) = 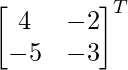
= 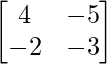
To Prove, (adj A)A = |A|I = A(adj A)
(adj A)A = 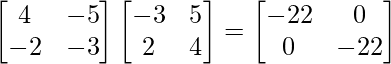
|A|I = 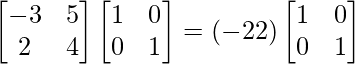 =
= 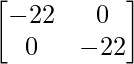
A(adj A) = 
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
(ii) 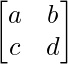
Solution:
Here, A = 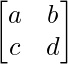
Cofactors of A are:
C11 = d C12 = -c
C21 = -b C22 = a
(adj A) =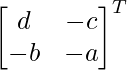
= 
To Prove, (adj A)A = |A|I = A(adj A)
(adj A)A = 
|A|I =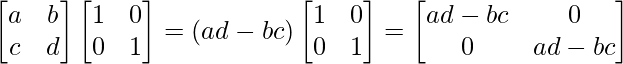
A(adj A) =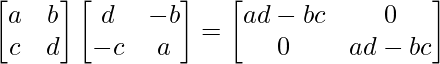
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
(iii) 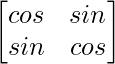
Solution:
Here, A = 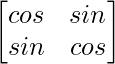
Cofactors of A are:
C11 = cos α C12 = -sin α
C21 = -sin α C22 = cos α
(adj A) =
=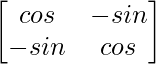
To Prove, (adj A)A = |A|I = A(adj A)
(adj A)A = 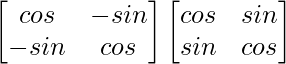
=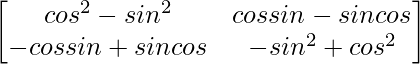
=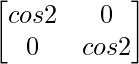
|A|I = 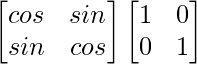
=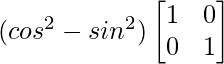
=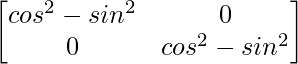
=
A(adj A) = 
=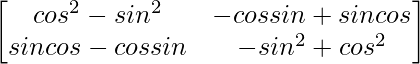
=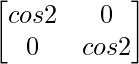
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
(iv) 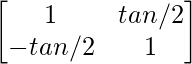
Solution:
Here, A = 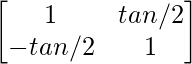
Cofactors of A are:
C11 = 1 C12 = -(-tan α/2) = tan α/2
C21 = -tan α/2 C22 = 1
adj A = 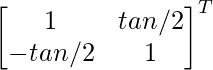
=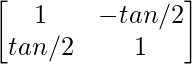
To Prove, (adj A)A = |A|I = A(adj A)
|A| = 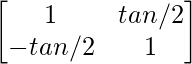
= 1 + tan2 α/2
= sec2α/2
(adj)A = 
=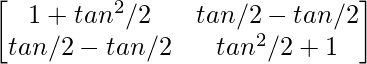
=
|A|I = (sec2α/2)
=
A(adj A) = 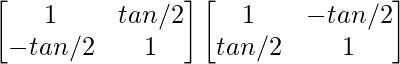
=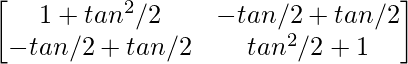
=
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
Question 2. Compute the adjoint of each of the following matrices:
Verify that (adj A)A = |A|I = A(adj A) for the above matrices:
(i) 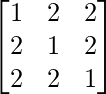
Solution:
Here, A = 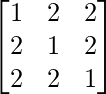
Cofactors of A are
C11 = 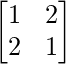 = -3
= -3
C21 =  = 2
= 2
C31 =  = 2
= 2
C12 =  = 2
= 2
C22 =  =-3
=-3
C32 = 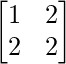 = 2
= 2
C13 = 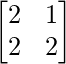 = 2
= 2
C23 =  = 2
= 2
C33 =  = -3
= -3
adj A = 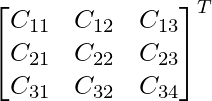
=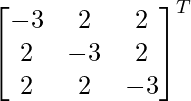
=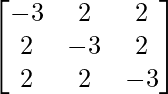
To Prove, (adj A)A = |A|I = A(adj A)
|A| = -3 + 4 + 4 = 5
(adj A)A = 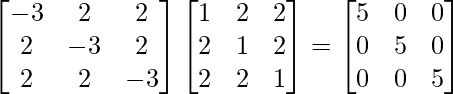
|A|I= (5)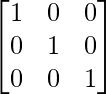 =
= 
A(adj A) = 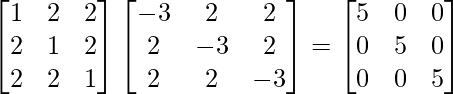
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
(ii) 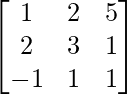
Solution:
Here, A = 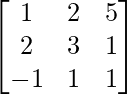
Cofactors of A are
C11 = 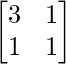 = 2
= 2
C12 = 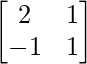 = -3
= -3
C13 = 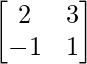 = 5
= 5
C21 = 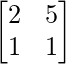 = 3
= 3
C22 =  = 6
= 6
C23 = 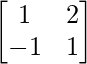 = -3
= -3
C31 =  = -13
= -13
C32 =  = 9
= 9
C33 = 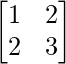 = -1
= -1
adj A = 
= 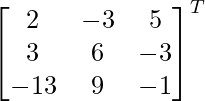
=
To Prove, (adj A)A = |A|I = A(adj A)
|A| = 1(3 – 1) – 2(2 + 1) + 5(2 + 3)
= 2 – 6 + 25 = 21
(adj A)A = 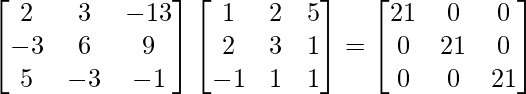
|A|I = (21)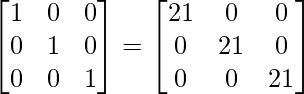
A(adj A) = 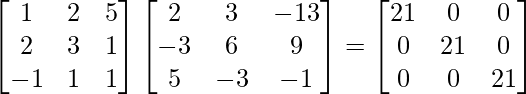
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
(iii) 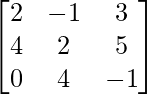
Solution:
Here, A = 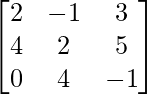
Cofactors of A are
C11 = 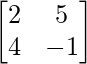 = -22
= -22
C12 = –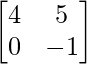 = 4
= 4
C13 =  = 16
= 16
C21 = – = 11
= 11
C22 = 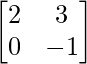 = -2
= -2
C23 = –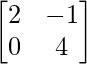 = -8
= -8
C31 = 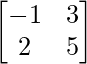 = -11
= -11
C32 = – = 2
= 2
C33 = 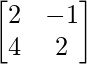 = 8
= 8
adj A = 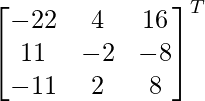
= 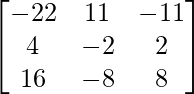
To Prove, (adj A)A = |A|I = A(adj A)
|A| = 2(-2 – 20) + 1(-4 – 0) + 3(16 – 0)
= -44 – 4 + 48 = 0
(adj A)A = 
|A|I = 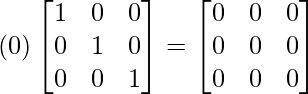
A(adj A) = 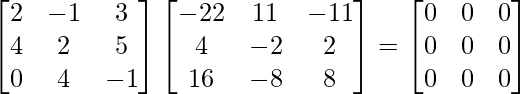
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
(iv) 
Solution:
Here, A = 
Cofactors of the A are
C11 =  = 3
= 3
C12 = – = -15
= -15
C13 =  = 4
= 4
C21 = 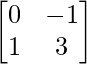 = -1
= -1
C22 = 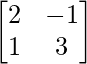 = 7
= 7
C23 =  = -2
= -2
C31 = 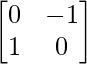 = 1
= 1
C32 = 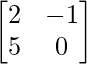 = -5
= -5
C33 = = 2
= 2
adj A = 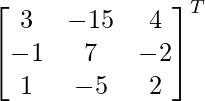
=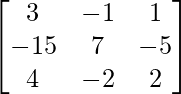
To Prove, (adj A)A = |A|I = A(adj A)
|A| = 2(3 – 0) – 0(15 – 0) – 1(5 – 1)
= 6 – 4 = 2
(adj A)A = 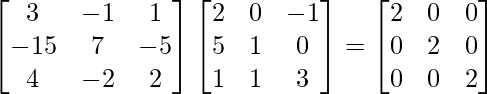
|A|I = (2)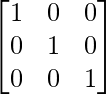
A (adj A) = 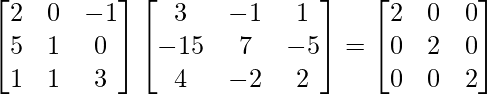
Therefore, (adj A)A = |A|I = A(adj A)
Hence Proved
Question 3. For the matrix A =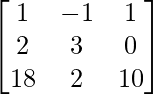 , show that A(adj A) = O.
, show that A(adj A) = O.
Solution:
Cofactor of A are,
C11 = 30 C12 = -20 C13 = -50
C21 = 12 C22 = -8 C23 = -20
C31 = -3 C32 = 2 C33 = 5
adj A = 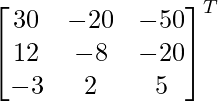
=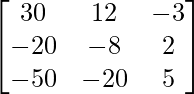
A(adj A) = 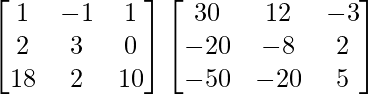
=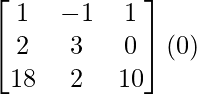
= 0
Hence Proved
Question 4. If A =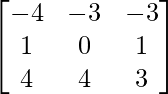 , show that adj A = A.
, show that adj A = A.
Solution:
Here, A =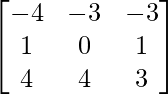
Cofactor of A are,
C11 = -4 C12 = 1 C13 = 4
C21 = -3 C22 = 0 C23 = 4
C31 = 4 C32 = 4 C33 = 3
adj A = 
=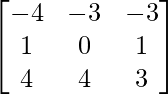
Therefore, adj A = A
Question 5. If A = 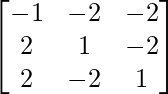 , show that adj A = 3AT.
, show that adj A = 3AT.
Solution:
Here, A = 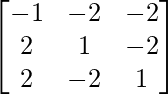
Cofactor of A are,
C11 = -3 C12 = -6 C13 = -6
C21 = 6 C22 = 3 C23 = -6
C31 = 6 C32 = -6 C33 = 3
adj A = 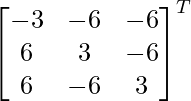
=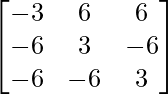
AT=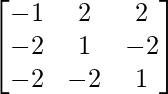
Now, 3AT = 3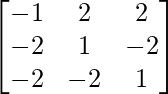 =
=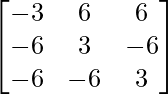
adj A = 3.AT
Hence Proved
Question 6. Find A(adj A) for the matrix A =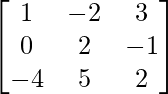 .
.
Solution:
Here, A =
Cofactor of A are,
C11 = 9 C12 = 4 C13 = 8
C21 = 19 C22 = 14 C23 = 3
C31 = -4 C32 = 1 C33 = 2
adj A = 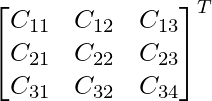
=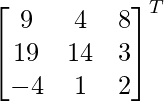
=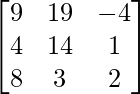
A(adj A) = 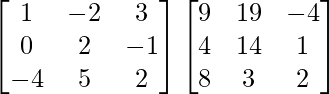
= 
= 25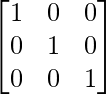
= 25I3
Question 7. Find the inverse of each of the following matrices:
(i) 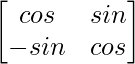
Solution:
Here, A = 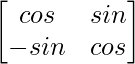
|A| = cos2θ + sin2θ = 1
Hence, inverse of A exist
Cofactors of A are,
Cofactor of A are,
C11 = cos θ C12 = sin θ
C21 = -sin θ C22 = cos θ
adj A = 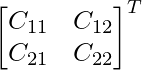
= 
= 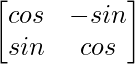
A-1 = 1/|A|. adj A
=1/1. 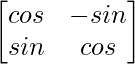
(ii) 
Solution:
Here, A = 
|A| = -1
Hence, inverse of A exist
Cofactor of A are,
C11 = 0 C12 = -1
C21 = -1 C22 = 0
adj A = 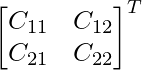
= 
= 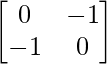
A-1 = 1/|A|. adj A
= 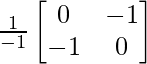
= 
(iii) 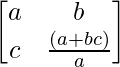
Solution:
Here, A = 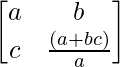
|A| = a(1 + bc)/a – bc = 1 + bc – bc = 1
Hence, inverse of A exists.
Cofactor of A are,
C11 = (1 + bc)/a C12 = -c
C21 = -b C22 = a
adj A =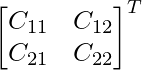
= 
= 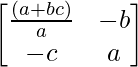
A-1 = 1/|A|. adj A
= 1/1 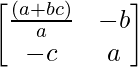
= 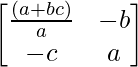
(iv) 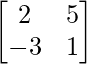
Solution:
Here, A = 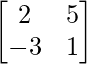
|A| = 2 + 15 = 17
Hence, inverse of A exists.
Cofactor of A are,
C11 = 1 C12 = 3
C21 = -5 C22 = 2
adj A = 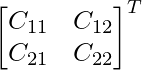
= 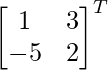
= 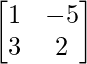
A-1 = 1/|A|. adj A
= 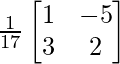
= 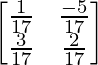
Question 8. Find the inverse of each of the following matrices.
(i) 
Solution:
Here, A =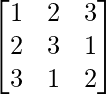
|A| = 1(6 – 1) – 2(4 – 3) + 3(2 – 9)
= 5 – 2 – 21 = -18
Therefore, inverse of A exists
Cofactors of A are:
C11 = 5 C12 = -1 C13 = -7
C21 = -1 C22 = -7 C23 = 5
C31 = -7 C32 = 5 C33 = -1
adj A = 
= 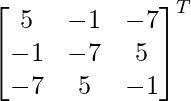
= 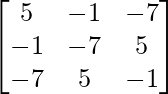
A-1 = 1/|A|. adj A
Hence, A-1 = 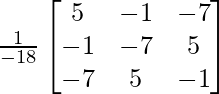
=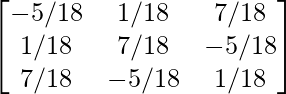
(ii) 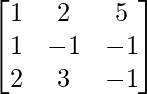
Solution:
Here, A = 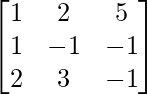
|A| = 1(1 + 3) – 2(-1 + 2) + 5(3 + 2)
= 4 – 2 – 25 = 27
Therefore, inverse of A exists
Cofactors of A are:
C11 = 4 C12 = -1 C13 = 5
C21 = -17 C22 = -11 C23 = 1
C31 = 3 C32 = 6 C33 = -3
adj A = 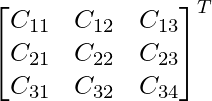
= 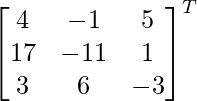
= 
A-1 = 1/|A|. adj A
Hence, A-1 = 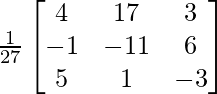
= 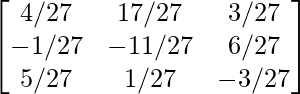
= 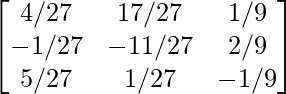
(iii) 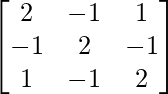
Solution:
Here, A =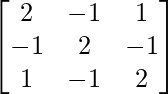
|A| = 2(4 – 1) – (-1)(-2 + 1) + 1(1 – 2)
= 6 – 1 – 1 = 4
Therefore, inverse of A exists
Cofactors of A are:
C11 = 3 C12 = 1 C13 = -1
C21 = 1 C22 = 3 C23 = 1
C31 = -1 C32 = 1 C33 = 3
adj A = 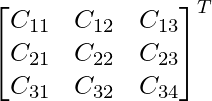
= 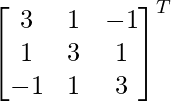
= 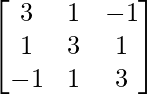
A-1 = 1/|A|. adj A
Hence, A-1 = 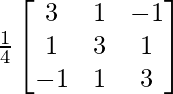
= 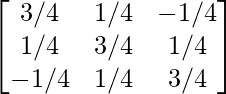
(iv) 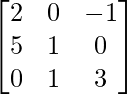
Solution:
Here, A =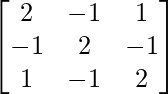
|A| = 2(3 – 0) – 0 + 1(5)
= 6 – 5 = 1
Therefore, inverse of A exists
Cofactors of A are:
C11 = 3 C12 = -15 C13 = 5
C21 = -1 C22 = 6 C23 = -2
C31 = 1 C32 = -5 C33 = 2
adj A = 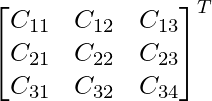
= 
= 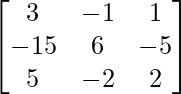
A-1 = 1/|A|. adj A
Hence, A-1 = 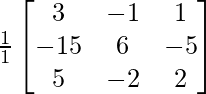
= 
(v) 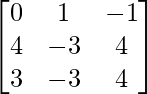
Solution:
Here, A = 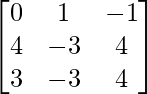
|A| = 0 – 1(16 – 12) – 1(-12 + 9)
= -4 + 3 = -1
Therefore, inverse of A exists
Cofactors of A are:
C11 = 0 C12 = -4 C13 = -3
C21 = -1 C22 = 3 C23 = 3
C31 = 1 C32 = -4 C33 = -4
adj A = 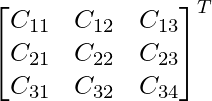
= 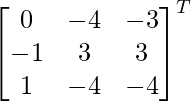
= 
A-1 = 1/|A|. adj A
Hence, A-1 = 
= 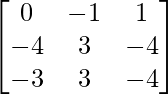
(vi) 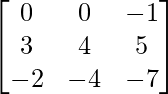
Solution:
Here, A = 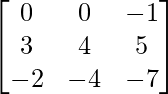
|A| = 0 – 0 – 1(-12 + 8)
= -1(-4) = 4
Therefore, inverse of A exists
Cofactors of A are:
C11 = -8 C12 = 11 C13 = -4
C21 = 4 C22 = -2 C23 = 0
C31 = 4 C32 = -3 C33 = 0
adj A = 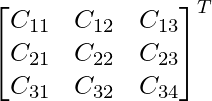
= 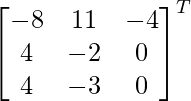
= 
A-1 = 1/|A|. adj A
Hence, A-1 = 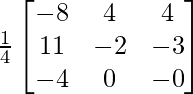
= 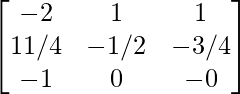
(vii) 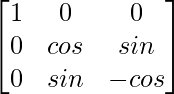
Solution:
Here, A = 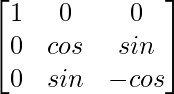
|A| = -cos2α – sin2α
= -(cos2α + sin2α) = -1
Therefore, inverse of A exists
Cofactors of A are:
C11 = -1 C12 = 0 C13 = -0
C21 = 0 C22 = -cosα C23 = -sinα
C31 = 0 C32 = -sinα C33 = cosα
adj A = 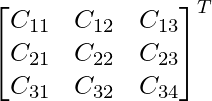
= 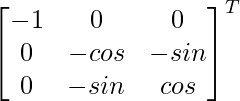
= 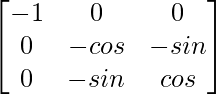
A-1 = 1/|A|. adj A
Hence, A-1 = 
= 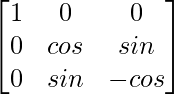
Question 9. (i) 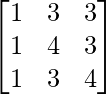
Solution:
Here, A = 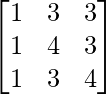
|A| = 1(16 – 9) – 3(4 – 3) + 3(3 – 4)
= 7 – 3 – 3 = 1
Therefore, inverse of A exists
Cofactors of A are:
C11 = 7 C12 = -1 C13 = -1
C21 = -3 C22 = 1 C23 = 0
C31 = -3 C32 = 0 C33 = 1
adj A = 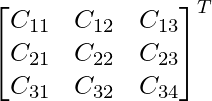
= 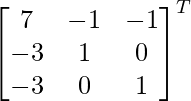
= 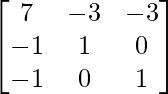
A-1 = 1/|A|. adj A
Hence, A-1 = 1/1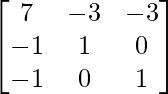
=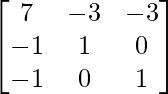
To verify A-1A = 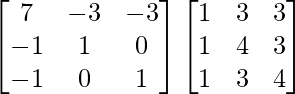
= 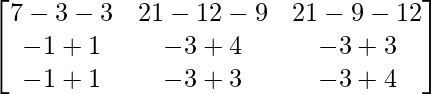
= 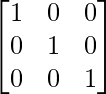
(ii) 
Solution:
Here, A = 
|A| = 2(8 – 7) – 3(6 – 3) + 1(21 – 12)
= 2 – 3(3) + 1(9) = 2
Therefore, inverse of A exists
Cofactors of A are:
C11 = 1 C12 = -3 C13 = 9
C21 = 1 C22 = 1 C23 = -5
C31 = -1 C32 = 1 C33 = -1
adj A = 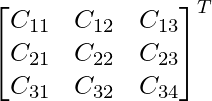
= 
= 
A-1 = 1/|A|. adj A
Hence, A-1 = 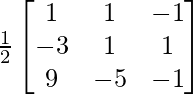
To verify A-1A = 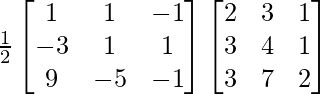
= 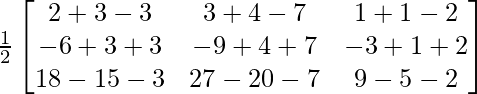
=
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...