Class 12 RD Sharma Solutions – Chapter 6 Determinants Exercise Ex. 6.6 | Set 2
Last Updated :
21 Jul, 2021
Question 19. Let A = [aij] be a square matrix of order 3 × 3 and Cij denote the cofactor of aij in A. If |A| = 5, find the value of a11 C21 + a12 C22 + a13 C23.
Solution:
As we know that, if a matrix is square matrix of order n, then the sum of the products of elements of a row or a column with the cofactors of the corresponding elements of some other row or column is zero.
So,
A = [aij] is a square matrix of order n.
Also we have,
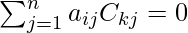
And 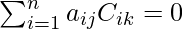
=> a11 C21 + a12 C22 + a13 C23 = 0
Therefore, the required value is 0.
Question 20. Find the value of 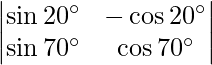 .
.
Solution:
Given that,
A = 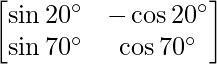
=> |A| = 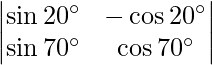
= sin 20° cos 70° + cos 20° sin 70°
= sin (20° + 70°)
= sin 90
= 1
Question 21. If A is a square matrix satisfying AT A = I, write the value of |A|.
Solution:
Let us assume that A = [aij] be a square matrix of order n.
So, by using the property of determinants, we get
=> |A| = |AT|
Here, we have
=> AT A = I
=> |AT A| = 1
So, the determinants are of same order, we get
=> |AT A| = |AT| |A|
=> |AT| |A| = 1
=> 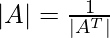
=> 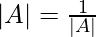
=> |A|2 = 1
=> |A| = ±1
Therefore, the value of |A| is ±1.
Question 22. If A and B are square matrices of the same order such that |A| = 3 and AB = I, then write the value of |B|.
Solution:
According to the question, A and B are square matrices of the same order.
So, by using the property of determinants we get,
=> |AB| = |A| |B|
Here, |A| = 3, AB = I.
=> |AB| = 1
=> |A| |B| = 1
=> 3 |B| = 1
=> |B| = 1/3
Therefore, the value of |B| is 1/3.
Question 23. A is a skew-symmetric of order 3, write the value of |A|.
Solution:
Here, |A| = 4.
So we have,
Order of the matrix (n) = 3
Using the properties of matrices, we get
For a square matrix of order n and constant k, we know,
=> |k A| = kn |A|
=> |- A| = (-1)3 |A|
= (-1) (4)
= -4
Therefore, the value of |A| is -4.
Question 24. If A is a square matrix of order 3 with determinant 4, then write the value of |−A|.
Solution:
Given that, |A| = 4.
Order of the matrix (n) = 3
So, by using the properties of matrices, we get
=> |k A| = kn |A|
=> |- A| = (-1)3 |A|
= (-1) (4)
= -4
Therefore, the value of |A| is -4.
Question 25. If A is a square matrix such that |A| = 2, write the value of |A AT|.
Solution:
Given that, |A| = 2
As we know that in a square matrix, |A| = AT
So, they are of sane order
Hence, |A AT| = |A| |AT|
=> |A AT| = 2 (2)
= 4
Therefore, the value of |A AT| is 4.
Question 26. Find the value of the determinant  .
.
Solution:
Given that,
A = 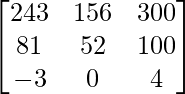
|A| = 
On applying R1 -> R1 – 3R2 we have,
= 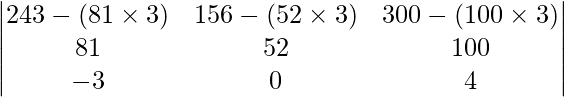
= 
= 0
Therefore, the value of the determinant is 0.
Question 27. Find the value of the determinant 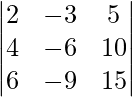 .
.
Solution:
Given that,
A = 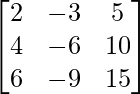
|A| = 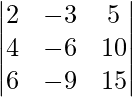
On applying R2 -> R2 – 2R1 we get,
= 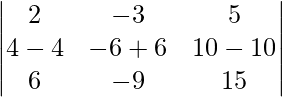
= 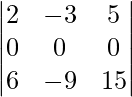
= 0
Therefore, the value of the determinant is 0.
Question 28. If the matrix 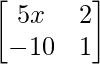 is singular, find the value of x.
is singular, find the value of x.
Solution:
As we know that a matrix is singular only when its determinant is zero.
According to the question,
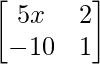 is a singular matrix
is a singular matrix
So,
=> |A| = 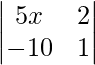 = 0
= 0
On expanding the determinant we get,
=> 5x + 20 = 0
=> x = -20/5
=> x = -4
Therefore, the value of x is -4.
Question 29. If A is a square matrix of order n × n such that |A| = λ, then write the value of |−A|.
Solution:
Given that,
A is a square matrix of order n × n
So, |A| = λ
=> |- A| = (-1)n A
=> |-A| = (-1)n λ
Therefore, the value of |-A| is (-1)n λ.
Question 30. Find the value of the determinant 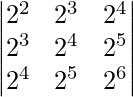 .
.
Solution:
Given that,
A = 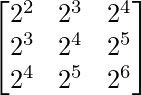
|A| = 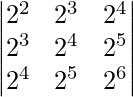
On taking out common factors from R1, R2 and R3 we get,
= 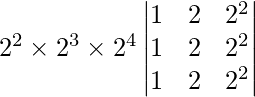
Here, the two rows are identical, so we get
= 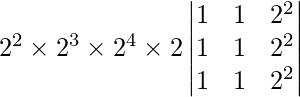
= 0
Therefore, the value of the determinant is 0.
Question 31. If A and B are non-singular matrices of the same order, prove whether AB is singular or non-singular.
Solution:
According to the question, A and B be non-singular matrices of order n.
Here, |A| ≠ 0 and |B| ≠ 0.
So, the order of these matrix are same, we get
=> |AB| = |A| |B|
=> |AB| = 0 if |A| = 0 or |B| = 0
But as it is not the case here, so |AB| is non- zero matrix and AB is non-singular matrix.
Hence proved.
Question 32. A matrix of order 3 × 3 has determinant 2. What is the value of |A (3I)|, where I is the identity matrix of order 3 × 3.
Solution:
Given that a matrix of order 3 x 3 has determinant 2.
So let us assume B be the matrix. so the order of the matrix is 3
and |B| = 2
Let us consider I be the identity matrix, so we get
=> |I| = 1
=> 3 |I| = 3
=> |A (3I)| = |3 A|
= 33 |A|
= 27 (2)
= 54
=> |A (3I)| = 54
Therefore, the value of |A (3I)| is 54.
Question 33. If A and B are square matrices of order 3 such that |A| = −1, |B| = 3, then find the value of |3 AB|.
Solution:
We have,
A and B are square matrices of order 3.
Also |A| = −1, |B| = 3.
We know,
As n is the order of A, we get
=> |K A| = Kn |A|
=> |3 AB| = 33 |AB|
If the order of A and B matrix are same and they are square matrix then |AB| = |A| |B|.
So, we have,
=> |3 AB| = 33 |A| |B|
= 27 (-1) (3)
= -81
Therefore, the value of |3 AB| is -81.
Question 34. Write the value of 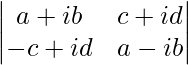 .
.
Solution:
We have,
A = 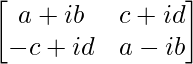
|A| = 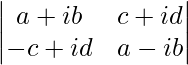
= a2 – iab + iab – i2 b2 – (-c2 – icd + icd + i2 d2)
= a2 – i2 b2 + c2 – i2 d2
Here, we have, i2 = – 1.
So we get,
|A| = a2 – (-1) b2 + c2 – (-1) d2
= a2 + b2 + c2 + d2
Therefore, the value is a2 + b2 + c2 + d2.
Question 35. Write the cofactor of a12 in the following matrix 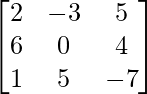 .
.
Solution:
We have
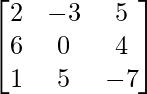
So,
=> a12 = -3
Now we find the cofactor of a12
a12 = (-1)1+2 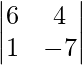
= – (- 42 – 4)
= 46
Therefore, the value of the required cofactor is 46.
Question 36. If 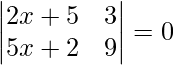 , find x.
, find x.
Solution:
Here we have,
A = 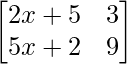
=> |A| = 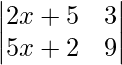 = 0
= 0
=> 9(2x + 5) – 3(5x + 2) = 0
=> 18x + 45 – 15x – 6 = 0
=> 3x + 39 = 0
=> 3x = – 39
=> x = -39/3
=> x = -13
Therefore, the value of x is -13.
Question 37. Find the value of x from the following : 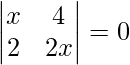
Solution:
We have,
A = 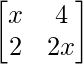
|A| = 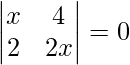
=> 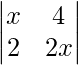 = 0
= 0
=> 2 x2 – 8 = 0
=> 2 x2 = 8
=> x2 = 8/2
=> x2 = 4
=> x = √4
=> x = ±2
Therefore, the value of x is ±2.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...