Class 12 RD Sharma Solutions – Chapter 6 Determinants Exercise Ex. 6.6 | Set 1

Last Updated : 07 Sep, 2021

Question 1. If A is a singular matrix, then find the value of |A|.

Solution:

Given that A is a singular matrix.

So, as we know if A is a n×n matrix and it is singular, the value of its determinant is always 0.

Thus, |A| = 0.

Question 2. For what value of x, the following matrix is singular?

$\begin{bmatrix}5 - x & x + 1 \\ 2 & 4\end{bmatrix}$

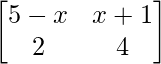
Solution:

Given that 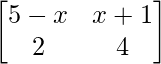$\begin{bmatrix}5 - x & x + 1 \\ 2 & 4\end{bmatrix}$

As we know if A is a n×n matrix and it is singular, so, the value of its determinant is always 0.

=> |A| = 0

=> $\begin{vmatrix}5 - x & x + 1 \\ 2 & 4\end{vmatrix} = 0$

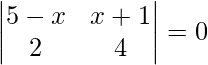
=> 4(5 – x) – 2(x + 1) = 0

=> 20 – 4x – 2x – 2 = 0

=> 18 – 6x = 0

=> 18 = 6x

=> x = 3

Therefore, the value of x is 3.

Question 3. Find the value of the determinant 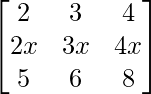$\begin{bmatrix}2 & 3 & 4 \\ 2x & 3x & 4x \\ 5 & 6 & 8\end{bmatrix}$ .

Solution:

Given that

A = $\begin{bmatrix}2 & 3 & 4 \\ 2x & 3x & 4x \\ 5 & 6 & 8\end{bmatrix}$

|A| = $\begin{vmatrix} 2 & 3 & 4\\ 2x & 3x & 4x \\ 5 & 6 & 8 \end{vmatrix}$

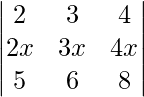
So, on taking out x common from R₂ we get,

|A| = 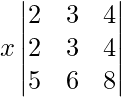$x\begin{vmatrix} 2 & 3 & 4\\ 2 & 3 & 4 \\ 5 & 6 & 8 \end{vmatrix}$

As R₁ = R₂, we get

|A| = 0

Therefore, the value of the determinant is 0.

Question 4. State whether the matrix 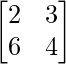$\begin{bmatrix}2 & 3 \\ 6 & 4\end{bmatrix}$ is singular or non-singular.

Solution:

Given that

A = 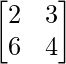$\begin{bmatrix}2 & 3 \\ 6 & 4\end{bmatrix}$

|A| = $\begin{vmatrix}2 & 3 \\ 6 & 4\end{vmatrix}$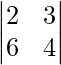

|A| = 2 (4) – 6 (3)

= 8 – 18

= -10

As we know if A is a n×n matrix and it is singular, so the value of its determinant is always 0.

As |A| = -10 here, the given matrix is non-singular.

Question 5. Find the value of the determinant 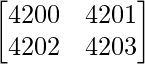$\begin{bmatrix}4200 & 4201 \\ 4202 & 4203\end{bmatrix}$ .

Solution:

Given that

A = 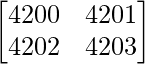$\begin{bma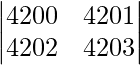trix}4200 & 4201 \\ 4202 & 4203\end{bmatrix}$

|A| = $\begin{vmatrix}4200 & 4201 \\ 4202 & 4203\end{vmatrix}$

On applying C₂ -> C₂ – C₁, we get

|A| = 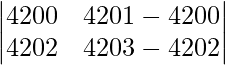$\begin{vmatrix}4200 & 4201-4200 \\ 4202 & 4203-4202\end{vmatrix}$

|A| = $\begin{vmatrix} 4200 & 1\\4202 & 1 \end{vmatrix}$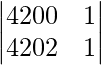

|A| = 4200 – 4202

|A| = -2

Therefore, the value of determinant is -2.

Question 6. Find the value of the determinant 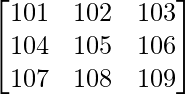$\begin{bmatrix}101 & 102 & 103 \\ 104 & 105 & 106 \\ 107 & 108 & 109\end{bmatrix}$ .

Solution:

Given that

A = 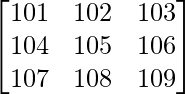$\begin{bma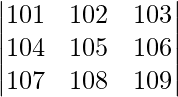trix}101 & 102 & 103 \\ 104 & 105 & 106 \\ 107 & 108 & 109\end{bmatrix}$

|A| = $\begin{vmatrix}101 & 102 & 103 \\ 104 & 105 & 106 \\ 107 & 108 & 109\end{vmatrix}$

On applying C₂ -> C₂ – C₁ and C₃ -> C₃ – C₁, we get

|A| = $\begin{vmatrix}101 & 102-101 & 103-101 \\ 104 & 105-104 & 106-104 \\ 107 & 108-107 & 109-107\end{vmatrix}$

|A| = $\begin{vmatrix} 101 & 1 & 2\\104 & 1 & 2\\107 & 1 & 2 \end{vmatrix}$

On taking out 2 common from R₃ we get,

|A| = 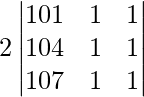$2\begin{vmatrix} 101 & 1 & 1\\104 & 1 & 1\\107 & 1 & 1 \end{vmatrix}$

As R₂ = R₃, we get

|A| = 0

Therefore, the value of the determinant is zero.

Question 7. Find the value of the determinant 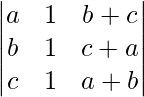$\begin{vmatrix}a & 1 & b + c \\ b & 1 & c + a \\ c & 1 & a + b\end{vmatrix}$ .

Solution:

Given that

A = $\begin{bmatrix}a & 1 & b + c \\ b & 1 & c + a \\ c & 1 & a + b\end{bmatrix}$

|A| = $\begin{vmatrix}a & 1 & b + c \\ b & 1 & c + a \\ c & 1 & a + b\end{vmatrix}$

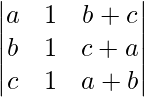
On applying C₁ -> C₁+ C₃ we get,

= $\begin{vmatrix} a + b + c & 1 & b + c\\a + b + c & 1 & c + a\\a + b + c & 1 & a + b \end{vmatrix}$

= $a + b + c \begin{vmatrix} 1 & 1& b + c\\1 & 1 & c + a\\1 & 1 & a + b \end{vmatrix}$

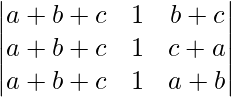
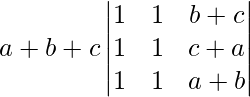
= (a + b + c) (0)

= 0

Therefore, the value of determinant is 0.

Question 8. If A = 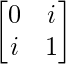$\begin{bmatrix}0 & i \\ i & 1\end{bmatrix}$ and B = $\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}$ , find the value of |A| + |B|.

Solution:

Given that

A = 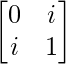$\begin{bma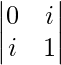trix} 0 & i\\i & 1 \end{bmatrix}$

|A| = $\begin{vmatrix} 0 & i\\i & 1 \end{vmatrix}$

= 0 – i²

= – (-1)

= 1

Also, we have

B = $\b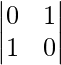egin{bmatrix} 0 & 1\\1 & 0 \end{bmatrix}$

|B| = $\begin{vmatrix} 0 & 1\\1 & 0 \end{vmatrix}$

= 0 – 1

= -1

So,

|A| + |B| = 1 + (-1)

= 1 – 1

= 0

Therefore, the value of |A| + |B| is 0.

Question 9. If A = 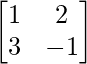$\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$ and B = 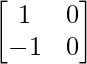$\begin{bmatrix}1 & 0 \\ - 1 & 0\end{bmatrix}$ , find |AB|.

Solution:

We have,

A = 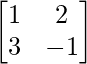$\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$ and B =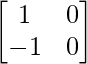 $\begin{bmatrix}1 & 0 \\ - 1 & 0\end{bmatrix}$

So, we get

AB = 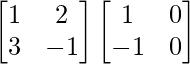$\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}\begin{bmatrix}1 & 0 \\ - 1 & 0\end{bmatrix}$

= $\begin{bmatrix}1 - 2 & 0 + 0 \\ 3 + 1 & 0 + 0\end{bmatrix}$

= $\begin{bmatrix}- 1 & 0 \\ 4 & 0\end{bmatrix}$

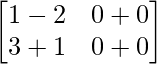
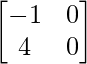
Now we have,

|AB| = 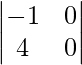$\begin{vmatrix}- 1 & 0 \\ 4 & 0\end{vmatrix}$

= -1 (0) – 0 (4)

= 0 – 0

= 0

Therefore, the value of |AB| is 0.

Question 10. Evaluate 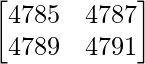$\begin{bmatrix}4785 & 4787 \\ 4789 & 4791\end{bmatrix}$ .

Solution:

Given that

A = 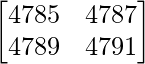$\begin{bma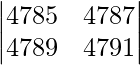trix}4785 & 4787 \\ 4789 & 4791\end{bmatrix}$

|A| = $\begin{vmatrix}4785 & 4787 \\ 4789 & 4791\end{vmatrix}$

On applying C₂ -> C₂ – C₁ we get,

|A| = 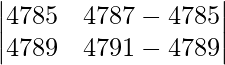$\begin{vmatrix}4785 & 4787-4785 \\ 4789 & 4791-4789\end{vmatrix}$

= $\begin{vmatrix}4785 & 2\\ 4789 & 2\end{vmatrix}$

On taking out 2 common from R₂ we get,

= $2 \times \begin{vmatrix}4785 & 1\\ 4789 & 1\end{vmatrix}$

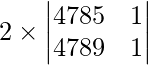
= 2 (4785 – 4789)

= 2 (-4)

= -8

Therefore, the value of the determinant is 0.

Question 11. If w is an imaginary cube root of unity, find the value of 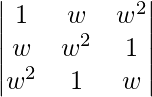$\begin{vmatrix}1 & w & w^2 \\ w & w^2 & 1 \\ w^2 & 1 & w\end{vmatrix}$ .

Solution:

Given that,

A = 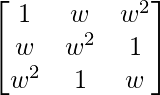$\begin{bma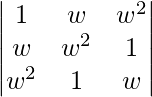trix}1 & w & w^2 \\ w & w^2 & 1 \\ w^2 & 1 & w\end{bmatrix}$

|A| = $\begin{vmatrix}1 & w & w^2 \\ w & w^2 & 1 \\ w^2 & 1 & w\end{vmatrix}$

On applying C₁ -> C₁ + C_{_2} + C_{_3} we get,

= $\begin{vmatrix} 1 + w + w^2 & w & w^2 \\ w + w^2 + 1 & w^2 & 1\\ w^2 + 1 + w & 1 & w \end{vmatrix}$

= $\begin{vmatrix} 0 & w& 7 w^2 \\ 0 & w^2 & 1\\ 0 & 1 & 7 w \end{vmatrix}$

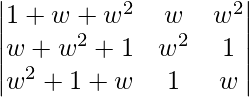
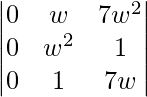
= 0

Question 12. If A = 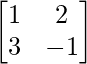$\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$ and B = $\begin{bmatrix}1 & - 4 \\ 3 & - 2\end{bmatrix}$ , find |AB|.

Solution:

Given that

A = 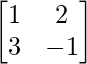$\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$

|A| = -1 – 6

= -7

B = $\begin{bmatrix}1 & - 4 \\ 3 & - 2\end{bmatrix}$

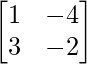
|B| = – 2 + 12

= 10

We know if A and B are square matrices of the same order, then we have,

=> |AB| = |A|. |B|

= (-7) (10)

= -70

Therefore, the value of |AB| is -70.

Question 13. If A = [a_ij] is a 3 × 3 diagonal matrix such that a₁₁ = 1, a₂₂ = 2 a₃₃ = 3, then find |A|.

Solution:

Given that a₁₁ = 1, a₂₂ = 2 and a₃₃ = 3.

If A is a diagonal matrix of order n x n, then we have

=> $\left| A \right| = a_{11} \times a_{22} \times a_{33} \times . . . \times a_{nn}$

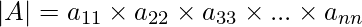
So, we get

|A| = 1 (2) (3)

= 6

Therefore, the value of |A| is 6.

Question 14. If A = [a_ij] is a 3 × 3 scalar matrix such that a₁₁ = 2, then find the value of |A|.

Solution:

Given that A = [a_ij] which is a 3 × 3 scalar matrix and a₁₁ = 2,

As we know that a scalar matrix is a diagonal matrix, in which all the diagonal elements are equal to a given scalar number.

=> A = $\begin{bmatrix} 2 & 0 & 0\\0 & 2 & 0\\0 & 0 & 2 \end{bmatrix}$

= $\begin{vmatrix} 2 & 0 & 0\\0 & 2 & 0\\ 0 & 0 & 2 \end{vmatrix}$

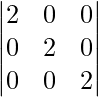
On expanding along C₁, we get

= $2 \times \begin{vmatrix} 2 & 0\\ 0 & 2 \end{vmatrix}$

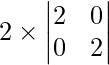
= 2 (2) (2)

= 8

Therefore, the value of |A| is 8.

Question 15. If I₃ denotes an identity matrix of order 3 × 3, find the value of its determinant.

Solution:

As we know that in an identity matrix, all the diagonal elements are 1 and the remaining elements are 0.

Here,

I₃ = 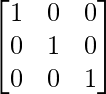$\begin{bmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1 \end{bmatrix}$

= $\begin{vmatrix} 1 & 0 & 0\\0 & 1 & 0\\0 & 0 & 1 \end{vmatrix}$

On expanding along C₁, we get

= $1 \times \begin{vmatrix} 1 & 0\\0 & 1 \end{vmatrix}$

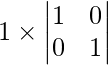
= 1

Therefore, the value of the determinant is 1.

Question 16. A matrix A of order 3 × 3 has determinant 5. What is the value of |3A|?

Solution:

Given that matrix A is of order 3 x 3 and the determinant = 5.

If A is a square matrix of order n and k is a constant, then we have

=> |kA| = kⁿ |A|

Here,

Number of rows = n

Also, k is a common factor from each row of k.

Hence, we get

3A = 3³ |A|

= 27 (5)

= 135

Therefore, the value of |3A| is 135.

Question 17. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [a_ij] is a₁₁ C₁₁ + a₁₂ C₁₂ + a₁₃ C₁₃, where [C_ij] is the cofactor of a_ij in A. Write the expression for its value on expanding by the second column.

Solution:

As we know that if a square matrix(let say A) is of order n, then the sum of the products of elements of a row or a column with their cofactors is always equal to det (A).

So,

$\sum^n_{i = 1} a_{i j} C_{i j} = \left| A \right|$

Also, $\sum^n_{j = 1} a_{i j} C_{i j} = \left| A \right|$

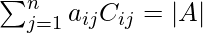
On expanding along R₁ we get,

|A| = a₁₁ C₁₁ + a₁₂C₁₂ + a₁₃ C₁₃

Now,

On expanding along C₂ we get,

|A| = a₁₂ C₁₂ + a₂₂ C₂₂+ a₃₂ C₃₂

Question 18. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [a_ij] is a₁₁ C₁₁ + a₁₂ C₁₂ + a₁₃ C₁₃, where [C_ij] is the cofactor of a_ij in A. Write the expression for its value on expanding by the second column.

Solution:

As we know that if a square matrix(let say A) is of order n, then the sum of the products of elements of a row or a column with their cofactors is always equal to det (A).

So,

$\sum^n_{i = 1} a_{i j} C_{i j} = \left| A \right|$

Also, $\sum^n_{j = 1} a_{i j} C_{i j} = \left| A \right|$

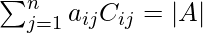
On expanding along R₁ we get,

|A| = a₁₁ C₁₁ + a₁₂ C₁₂ + a₁₃ C₁₃

Now,

On expanding along C₂ we get,

|A| = a₁₂ C₁₂ + a₂₂ C₂₂ + a₃₂ C₃₂ = 5

Suggest improvement

Class 12 RD Sharma Solutions- Chapter 33 Binomial Distribution - Exercise 33.2 | Set 1

Torque on an Electric Dipole in Uniform Electric Field

Share your thoughts in the comments

Class 12 RD Sharma Solutions – Chapter 6 Determinants Exercise Ex. 6.6 | Set 1

Question 1. If A is a singular matrix, then find the value of |A|.

Question 2. For what value of x, the following matrix is singular?

Question 3. Find the value of the determinant .

Question 4. State whether the matrix is singular or non-singular.

Question 5. Find the value of the determinant .

Question 6. Find the value of the determinant .

Question 7. Find the value of the determinant .

Question 8. If A = and B = , find the value of |A| + |B|.

Question 9. If A = and B = , find |AB|.

Question 10. Evaluate .

Question 11. If w is an imaginary cube root of unity, find the value of .

Question 12. If A = and B = , find |AB|.

Question 13. If A = [aij] is a 3 × 3 diagonal matrix such that a11 = 1, a22 = 2 a33 = 3, then find |A|.

Question 14. If A = [aij] is a 3 × 3 scalar matrix such that a11 = 2, then find the value of |A|.

Question 15. If I3 denotes an identity matrix of order 3 × 3, find the value of its determinant.

Question 16. A matrix A of order 3 × 3 has determinant 5. What is the value of |3A|?

Question 17. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [aij] is a11 C11 + a12 C12 + a13 C13, where [Cij] is the cofactor of aij in A. Write the expression for its value on expanding by the second column.

Question 18. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [aij ] is a11 C11 + a12 C12 + a13 C13, where [Cij] is the cofactor of aij in A. Write the expression for its value on expanding by the second column.

Please Login to comment...

Similar Reads

What kind of Experience do you want to share?

Question 3. Find the value of the determinant $\begin{bmatrix}2 & 3 & 4 \\ 2x & 3x & 4x \\ 5 & 6 & 8\end{bmatrix}$ .

Question 4. State whether the matrix $\begin{bmatrix}2 & 3 \\ 6 & 4\end{bmatrix}$ is singular or non-singular.

Question 5. Find the value of the determinant $\begin{bmatrix}4200 & 4201 \\ 4202 & 4203\end{bmatrix}$ .

Question 6. Find the value of the determinant $\begin{bmatrix}101 & 102 & 103 \\ 104 & 105 & 106 \\ 107 & 108 & 109\end{bmatrix}$ .

Question 7. Find the value of the determinant $\begin{vmatrix}a & 1 & b + c \\ b & 1 & c + a \\ c & 1 & a + b\end{vmatrix}$ .

Question 8. If A = $\begin{bmatrix}0 & i \\ i & 1\end{bmatrix}$ and B = $\begin{bmatrix}0 & 1 \\ 1 & 0\end{bmatrix}$ , find the value of |A| + |B|.

Question 9. If A = $\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$ and B = $\begin{bmatrix}1 & 0 \\ - 1 & 0\end{bmatrix}$ , find |AB|.

Question 10. Evaluate $\begin{bmatrix}4785 & 4787 \\ 4789 & 4791\end{bmatrix}$ .

Question 11. If w is an imaginary cube root of unity, find the value of $\begin{vmatrix}1 & w & w^2 \\ w & w^2 & 1 \\ w^2 & 1 & w\end{vmatrix}$ .

Question 12. If A = $\begin{bmatrix}1 & 2 \\ 3 & - 1\end{bmatrix}$ and B = $\begin{bmatrix}1 & - 4 \\ 3 & - 2\end{bmatrix}$ , find |AB|.

Question 13. If A = [a_ij] is a 3 × 3 diagonal matrix such that a₁₁ = 1, a₂₂ = 2 a₃₃ = 3, then find |A|.

Question 14. If A = [a_ij] is a 3 × 3 scalar matrix such that a₁₁ = 2, then find the value of |A|.

Question 15. If I₃ denotes an identity matrix of order 3 × 3, find the value of its determinant.

Question 17. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [a_ij] is a₁₁ C₁₁ + a₁₂ C₁₂ + a₁₃ C₁₃, where [C_ij] is the cofactor of a_ij in A. Write the expression for its value on expanding by the second column.

Question 18. On expanding by the first row, the value of the determinant of 3 × 3 square matrix A = [a_ij] is a₁₁ C₁₁ + a₁₂ C₁₂ + a₁₃ C₁₃, where [C_ij] is the cofactor of a_ij in A. Write the expression for its value on expanding by the second column.