Question 17. Solve the following system of the linear equations by Cramer’s rule.
2x − 3y − 4z = 29
−2x + 5y − z = −15
3x − y + 5z = −11
Solution:
Using Cramer’s Rule, we get,
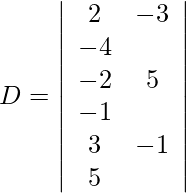
Expanding along R1, we get,
= 2 (24) + 3 (−13) + 4 (-13)
= 48 − 21 – 52
= -25
Also, we get,
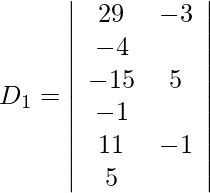
Expanding along R1, we get,
= 29 (24) + 3 (−64) + 4 (−40)
= 692 − 192 − 160
= 344
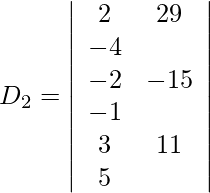
Expanding along R1, we get,
= 2 (−64) − 29 (−7) + 4 (23)
= −128 + 203 + 92
= 167
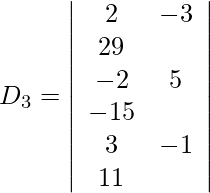
Expanding along R1, we get,
= 2 (40) + 3 (23) + 29 (−13)
= 80 + 69 − 377
= −228
So, x = D1/D = -344/25
y = D2/D = -167/25
z = D3/D = 228/25
Therefore, x = -344/25, y = -167/25, and z = 228/25.
Question 18. Solve the following system of the linear equations by Cramer’s rule.
x + y = 1
x + z = −6
x − y − 2z = 3
Solution:
Using Cramer’s Rule, we get,
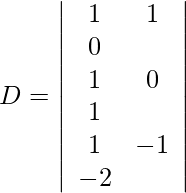
= 1(1) – 1(-3)
= 1 + 3
= 4
Also, we get,
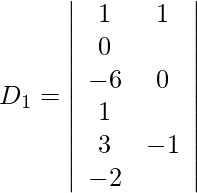
Expanding along R1, we get,
= 1 (1) − 1 (9) + 0
= 1 − 9
= −8
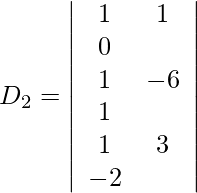
Expanding along R1, we get,
= 1 (9) − 1 (−3)
= 9 + 3
= 12
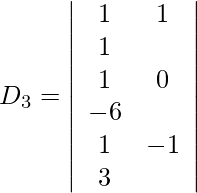
Expanding along R1, we get,
= 1 (−6) − 1 (9) + 1 (−1)
= −6 − 9 − 1
= −16
So, x = D1/D = -8/4 = -2
y = D2/D = 12/4 = 3
z = D3/D = -16/4 = -4
Therefore, x = −2, y = 3 and z = −4.
Question 19. Solve the following system of linear equations by Cramer’s rule.
x + y + z + 1 = 0
ax + by + cz + d = 0
a2x + b2y + c2z + d2 = 0
Solution:
Using Cramer’s Rule, we get,
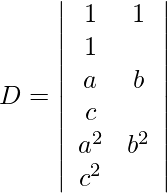
c2 -> c2 – c1, c3 -> c3 – c1
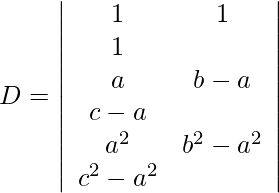
Taking common (b-a) from c2 and (c-a)c3
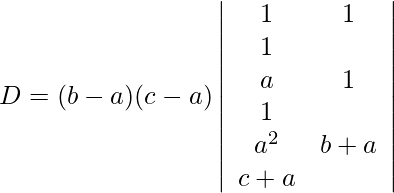
Expanding along R1, we get,
= (b – a)(c – a)(c + a – b – a)
= (b – a)(c – a)(c – b)
= (a – b)(b – c)(c – a)
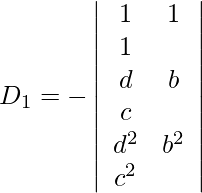
= -(d – b)(b – c)(c – d)
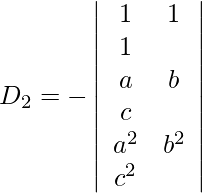
= -(a – d)(d – c)(c – a)
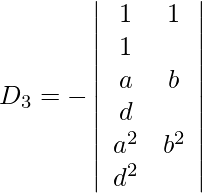
= -(a – d)(b – d)(d – a)
So, x = D1/D = -(d – b)(b – c)(c – d)/(a – b)(b – c)(c – a)
y = D2/D = -(a – d)(d – c)(c – a)/(a – b)(b – c)(c – a)
z = D3/D = -(a – d)(b – d)(d – a)/(a – b)(b – c)(c – a)
Question 20. Solve the following system of linear equations by Cramer’s rule.
x + y + z + w = 2
x − 2y + 2z + 2w = −6
2x + y − 2z + 2w = −5
3x − y + 3z − 3w = −3
Solution:
Using Cramer’s Rule, we get,
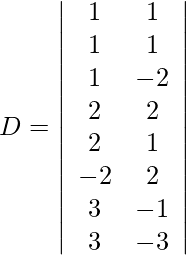
= 
= 
= −94
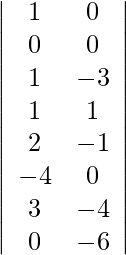
Also, we get,
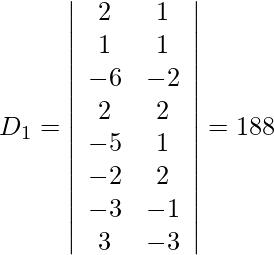
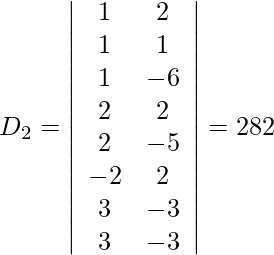
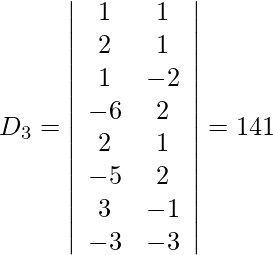
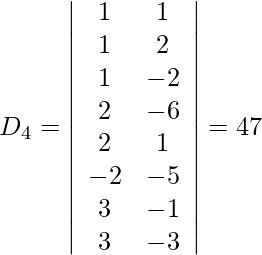
So, x = D1/D = -188/94 = -2
y = D2/D = -282/-94 = 3
z = D3/D = -141/-94 = 3/2
w = D4/D = -47/94 = -1/2
Therefore, x = −2, y = 3 and z = 3/2 and w = -1/2.
Question 21. Solve the following system of linear equations by Cramer’s rule.
2x − 3z + w = 1
x − y + 2w = 1
−3y + z + w = 1
x + y + z = −1
Solution:
Using Cramer’s Rule, we get,
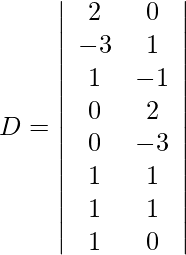
=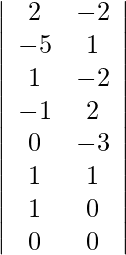
= 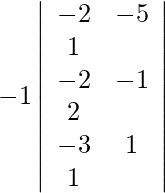
= −21
Also, we get,
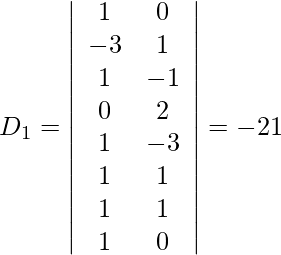
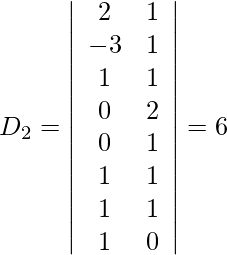
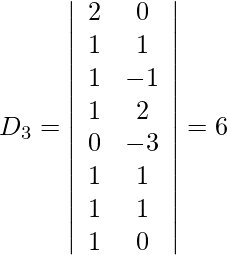
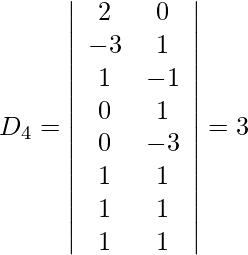
So, x = D1/D = -21/-21 = 1
y = D2/D = -6/-21 = 2/7
z = D3/D = -6/-21 = 2/7
w = D4/D = -3/21 = -1/7
Therefore, x = 1, y = 2/7 and z = 2/7 and w = -1/7.
Question 22. Show that the following system of linear equations is inconsistent.
2x − y = 5
4x − 2y = 7
Solution:
Using Cramer’s Rule, we get,
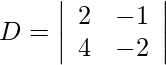
= −4 + 4
= 0
Also, we get,
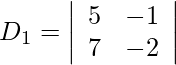
= − 10 + 7
= −3
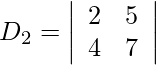
= 14 − 20
= −6
Since D = 0 and D1 and D2 both are non-zero, the given system of equations is inconsistent.
Hence proved.
Question 23. Show that the following system of linear equations is inconsistent.
3x + y = 5
−6x − 2y = 9
Solution:
Using Cramer’s Rule, we get,
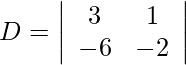
= −6 + 6
= 0
Also, we get,
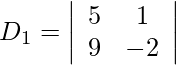
= −10 − 9
= −19
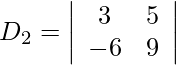
= 27 + 30
= 57
Since D = 0 and D1 and D2 both are non-zero, the given system of equations is inconsistent.
Hence proved.
Question 24. Show that the following system of linear equations is inconsistent.
3x − y + 2z = 3
2x + y + 3z = 5
x − 2y − z = 1
Solution:
Using Cramer’s Rule, we get,
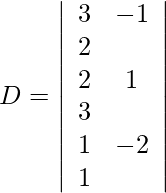
Expanding along R1, we get
= 3 (5) + 1 (−5) + 2 (−5)
= 15 − 5 − 10
= 0
Also, we get,
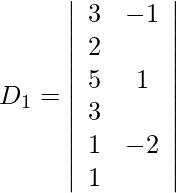
Expanding along R1, we get
= 3 (5) + 1 (−8) + 2 (−11)
= 15 − 8 − 22
= −15
Since D = 0 and D1 are non-zero, the given system of equations is inconsistent.
Hence proved.
Question 25. Show that the following system of linear equations is consistent and solve.
3x − y + 2z = 6
2x − y + z = 2
3x + 6y + 5z = 20
Solution:
Using Cramer’s Rule, we get,
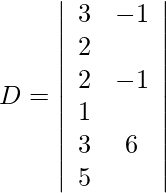
Expanding along R1, we get
= 3 (−11) + 1 (7) + 2 (15)
= −33 + 7 + 30
= 4
Also, we get,
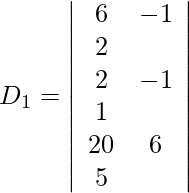
Expanding along R1, we get
= 6 (−11) + 1 (−10) + 2 (32)
= −66 − 10 + 64
= −12
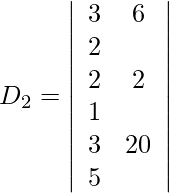
Expanding along R1, we get
= 3 (−10) − 6 (7) + 2 (34)
= −30 − 42 + 68
= −4
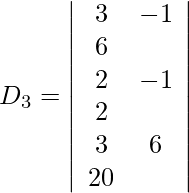
Expanding along R1, we get
= 3 (−32) + 1 (34) + 6 (15)
= −96 + 34 + 90
= 28
As D, D1, D2 and D3 all are non-zero, the given system of equations is consistent.
So, x = D1/D = -12/4 = -3
y = D2/D = -4/4 = -1
z = D3/D = 28/4 = 7
Therefore, x = −3, y = −1 and z = 7.
Question 26. Show that the following system of linear equations has infinite number of solutions.
x − y + z = 3
2x + y − z = 2
−x − 2y + 2z = 1
Solution:
Using Cramer’s Rule, we get,
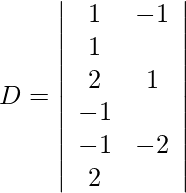
= 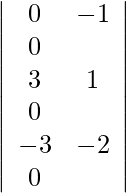
= 0
Also, we get,
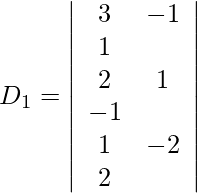
= 
= 0
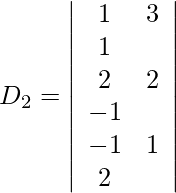
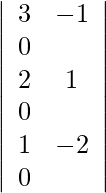
= 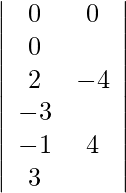
= 0
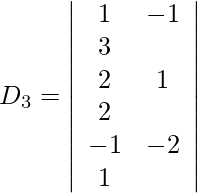
= 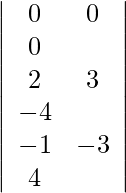
= 0
As D, D1, D2 and D3 all are zero, the given system of equations has infinite number of solutions.
Hence proved.
Question 27. Show that the following system of linear equations has infinite number of solutions.
x + 2y = 5
3x + 2y = 15
Solution:
Using Cramer’s Rule, we get,
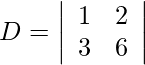
= 6 − 6
= 0
Also, we get,
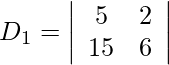
= 30 − 30
= 0
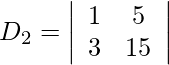
= 15 − 15
= 0
As D, D1 and D2 all are zero, the given system of equations has infinite number of solutions.
Hence proved.
Question 28. Show that the following system of linear equations has infinite number of solutions.
x + y − z = 0
x − 2y + z = 0
3x + 6y − 5z = 0
Solution:
Using Cramer’s Rule, we get,
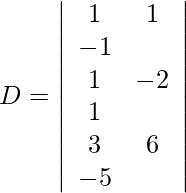
= 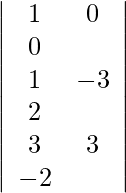
= 1 (6 − 6)
= 0
Also, we get,
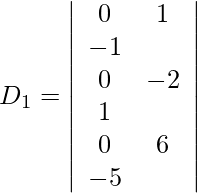
= 0
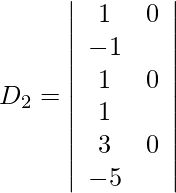
= 0
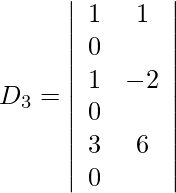
= 0
As D, D1, D2 and D3 all are zero, the given system of equations has infinite number of solutions.
Hence proved.
Question 29. Show that the following system of linear equations has infinite number of solutions.
2x + y − 2z = 4
x − 2y + z = −2
5x − 5y + z = −2
Solution:
Using Cramer’s Rule, we get,
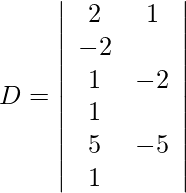
= 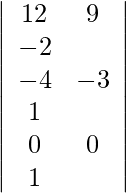
= 1 (−36 + 36)
= 0
Also we get,
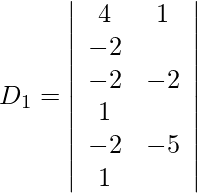
= 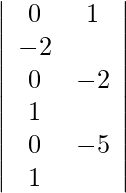
= 0
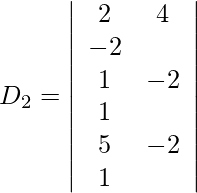
= 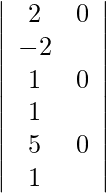
= 0
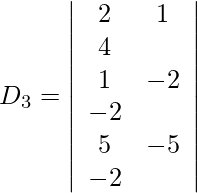
= 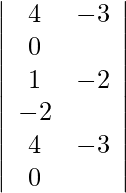
= 2 (−12 + 12)
= 0
As D, D1, D2 and D3 all are zero, the given system of equations has infinite number of solutions.
Hence proved.
Question 30. Show that the following system of linear equations has infinite number of solutions.
x − y + 3z = 6
x + 3y − 3z = −4
5x + 3y + 3z = 10
Solution:
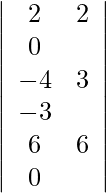
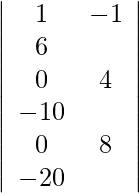
Using Cramer’s Rule, we get,
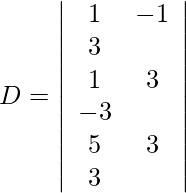
= 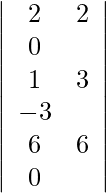
= 3 (12 − 12)
= 0
Also we get,
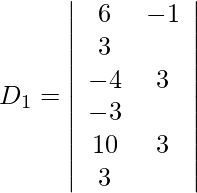
= 
= 3 (12 − 12)
= 0
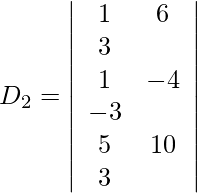
= 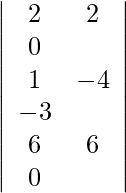
= 3 (12 − 12)
= 0
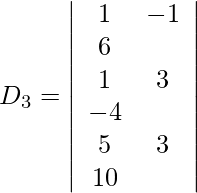
= 
= 1 (−80 + 80)
= 0
As D, D1, D2 and D3 all are zero, the given system of equations has infinite number of solutions.
Hence proved.
Question 31. A salesman has the following record of sales during three months for three items A, B and C which have different rates of commission.
| Month | Sale of units | Total Commission (in Rs) |
|---|
| A | B | C |
|---|
| Jan | 90 | 100 | 20 | 800 |
| Feb | 130 | 50 | 40 | 900 |
| Mar | 60 | 100 | 30 | 850 |
Find out the rates of commission on items A, B and C by using the determinant method.
Solution:
Let the rates of commission on items A, B and C be x, y and z respectively.
According to the question, we have,
90x + 100y + 20z = 800
130x + 50y + 40z = 900
60x + 100y + 30z = 850
Using Cramer’s Rule, we get,
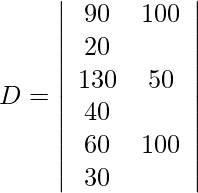
= 
= 50 (8500 − 12000)
= −175000
Also we get,
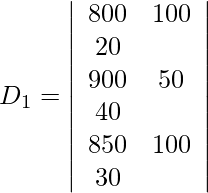
= 
= 50 (50000 − 57000)
= −350000
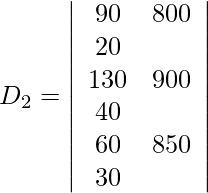
= 
= 20 (17500 − 52500)
= −700000
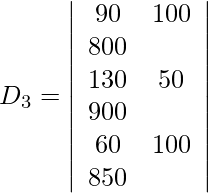
= 
= 50 (161500 − 200000)
= −1925000
So, x = D1/D = -350000/-175000 = 2
y = D2/D = -700000/-175000 = 4
z = D3/D = -1925000/-175000 = 11
Therefore, the rates of commission on items A, B and C are 2%, 4% and 11% respectively.
Question 32. An automobile company uses three types of steel S1, S2, and S3 for producing three types of cars C1, C2 and C3. Steel requirements (in tons) for each type of cars are given below.
| Steel | Cars |
|---|
| C1 | C2 | C3 |
|---|
| S1 | 2 | 3 | 4 |
| S2 | 1 | 1 | 2 |
| S3 | 3 | 2 | 1 |
Using Cramer’s Rule, find the number of cars of each type which can be produced using 29, 13 and 16 tons of steel of three types respectively.
Solution:
Let x, y and z be the number of cars C1, C2 and C3 produced respectively.
According to the question, we have,
2x + 3y + 4z = 29
x + y + 2z = 13
3x + 2y + z = 16
Using Cramer’s Rule, we get,
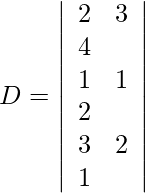
= 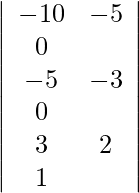
= 1 (30 − 25)
= 5
Also we get,
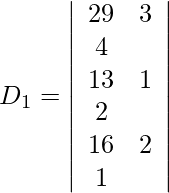
= 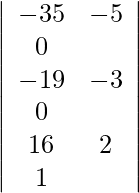
= 1 (105 − 95)
= 10
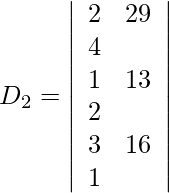
= 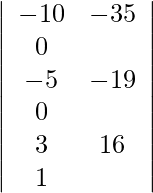
= 1 (190 − 175)
= 15
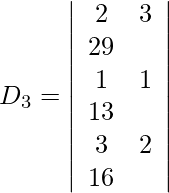
= 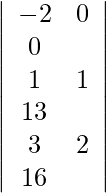
= −2 (16 − 26)
= 20
So, x = D1/D = 10/5 = 2
y = D2/D = 15/5 = 3
z = D3/D = 20/5 = 4
Therefore, the number of cars produced of type C1, C2 and C3 are 2, 3 and 4.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...